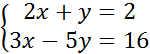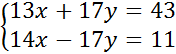Урок "Метод алгебраического сложения"

Методическая информация

Тип урока (мероприятия, занятия)

Урок новых знаний

Цели урока (мероприятия, занятия)

(образовательные, развивающие, воспитательные)

Образовательные

Создать условия для введения метода алгебраического сложения при решении систем двух уравнений с двумя переменными, для формирования умений использовать данный метод при решении задач.

Развивающие

Создать условия для развития алгоритмического мышления

Воспитательные

Создать условия для воспитания активной личности

Задачи урока (мероприятия, занятия)

создать условия для совершенствования умений:

формулировать цель, задачи, планировать, корректировать, оценивать свою деятельность,

осуществлять действия и поступки на основе выбранных целевых и смысловых установок,

для развития умений:

использовать метод алгебраического сложения при решении систем двух уравнений с двумя переменными,

выстраивать логические цепочки рассуждений при обосновании решений задач,

излагать точно, ясно, грамотно свои мысли в устной и письменной форме.

Используемые педагогические технологии,  методы и приемы

Технология проблемного обучения.

Деятельностный подход.

Прием самооценивания.

Время реализации урока (мероприятия, занятия)

40 минут

Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят/др. ученики в ходе урока (мероприятия, занятия)

Необходимое оборудование и материалы

ПК.

Мультимедийный проектор.

Дидактическое обеспечение урока (мероприятия, занятия)

Листы самооценки.

Карточка с алгоритмом решения систем двух уравнений методом подстановки.

Список учебной и дополнительной литературы

1. Алгебра. 7 класс. Ч. 2. Задачник для учащихся общеобразовательных учреждений / [А.Г. Мордкович и др.] под ред. А.Г. Мордковича. – М.: Мнемозина, 2010. – 223 с.

2. Мордкович А.Г. Алгебра. 7 класс. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2010. – 224 с.

Ход и содержание урока (мероприятия, занятия),

деятельность учителя и учеников.

Мотивация учащихся

Здравствуйте, ребята.

Сегодня наш урок я хотела начать с философской загадки Вальтера.

Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами? - Время.

Итак, у нас всего 40 минут и мне очень хотелось, чтобы это время пролетело для вас незаметно и с пользой.

Подробное описание всех этапов урока  (мероприятия, занятия).

Подготовительный этап

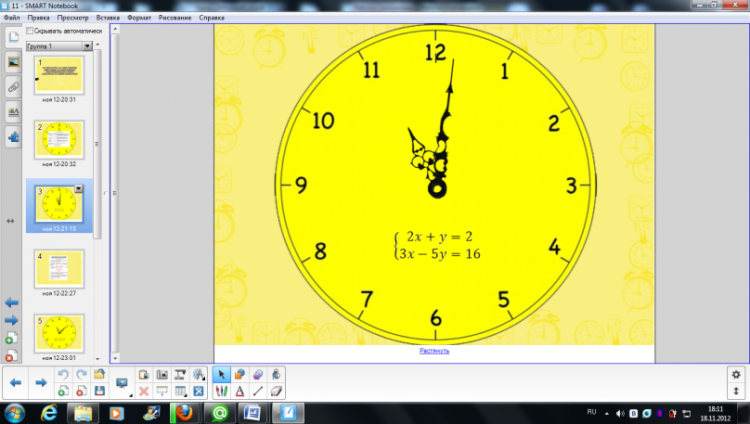
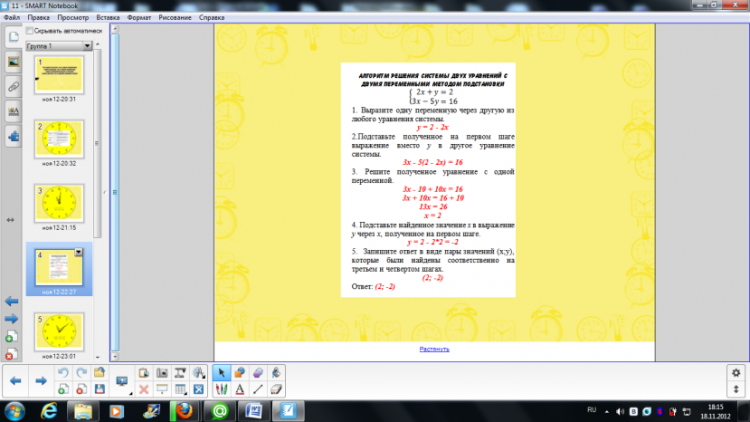
На каждом этапе урока вы будете самостоятельно оценивать свою работу с помощью листов самооценки. Запишите свои фамилию и имя  данный лист. В колонку отметка вам предстоит поставить балл, который будет соответствовать вашей работе. В этом вам помогут критерии, записанные в следующем столбце.

Посмотрит, пожалуйста, на слайд. Перед нами система двух уравнений.

Вспомним. как вы решали их на прошлом уроке.

Методом подстановки

У вас на партах лежат карточки, которые помогут вспомнить алгоритм решения системы двух уравнений с двумя переменными методом подстановки. Ваша задача прочесть пункт алгоритма и вписать рядом соответствующий шаг решения. На выполнение задания у вас 3 минуты. Приступайте.

Выполним проверку. Посмотрите на слайд и сравните свое решение с решением на слайде.

Оцените свою работу на данном этапе.

Найдите этап повторение и оцените свою работу по критериям, прописанным в листе самооценки.

Еще раз обратите внимание на решенную систему и скажите, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?

Уравнения системы с двумя переменными. Умеем решать уравнение с одной переменной.

Верно. Только получив уравнение с одной переменной нам удалось решить систему уравнений.

Стрелки наших часов передвинулись и мы приступаем к решению следующей системы.

Решение данной системы оформим в тетради. Откройте тетрадь, запишите число и данную систему. У вас есть алгоритм, который вы можете использовать.

Прочтите первый шаг алгоритма.

Выразите одну переменную через другую из любого уравнения системы.

Выберем уравнение, в котором удобно одну переменную выразить через другую.

Такого уравнения нет.

Т.е.  в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?

Найти новый метод.

Этап сообщения новых знаний

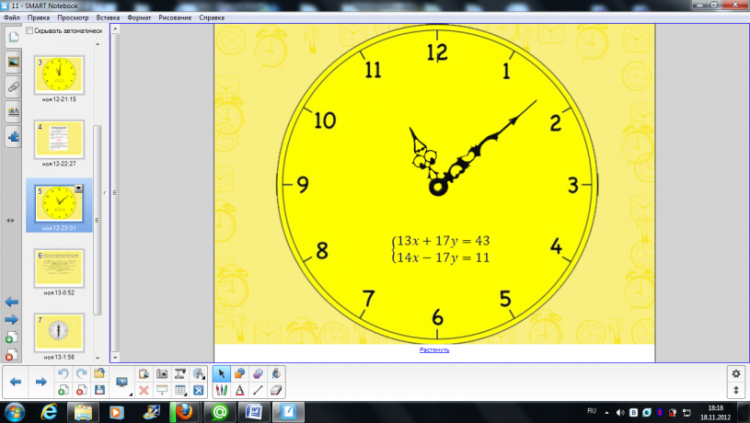
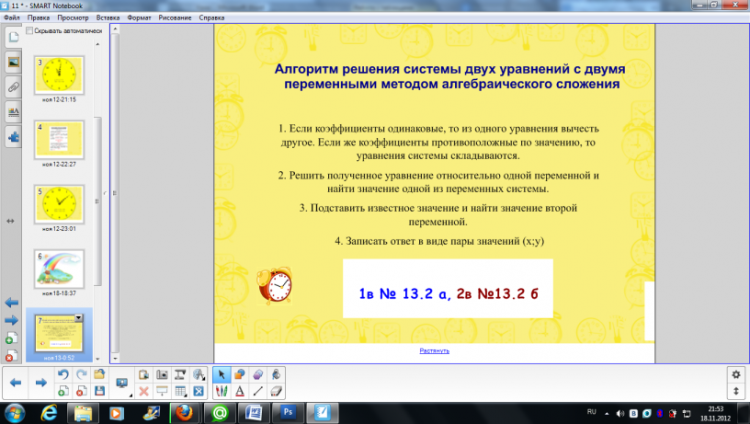
Попытаемся сформулировать цель урока.

Научиться решать системы новым методом.

Записать на доске.

Что нам необходимо сделать, чтобы научиться решать системы новым методом?

1. Алгоритм решения системы двух уравнений новым методом.

2. Практикум по решению систем.

3. Итог урока.

Оцените свою деятельность на 2 и 3 этапах урока.

Приступим к выведению нового метода.

Обратите внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось толь после того, как мы получили линейное уравнение с одной переменной.

Посмотрите на систему уравнений и подумайте, как из двух данных уравнений получить одно уравнение с одной переменной.

Сложить уравнения.

Что значит сложить уравнения?

По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.

Хорошо. Попробуем. Работаем вместе со мной.

13x+14x+17y-17y=43+11

13x+14x=43+11

Получили линейное уравнение с одной переменной.

27x=54

x=2

Решили систему уравнений?

Нет.

Почему?

Решение системы - пара чисел.

Как найти у?

Найденное значение х подставить в уравнение системы.

Имеет значение, в какое уравнение подставим значение х?

Да. Нет.

В первое уравнение подставят те, кто сидят на первом варианте. Во второе уравнение подставят те, кто сидят на втором варианте и  ответим на вопрос.

Значит найденное значение х можно подставить в ...

любое уравнение системы.

Мы с вами познакомились с новым методом - метод алгебраического сложения.

Решая систему, мы с вами проговорили алгоритм решения системы данным методом.

Проговорим шаги алгоритма еще раз.

Хорошо. Представим алгоритм на слайде, чтобы использовать его при решении систем.

Вернемся к слайду с планом урока. 

Алгоритм мы с вами рассмотрели. Теперь применим его к решению задач.

Оцените свою работу на данном этапе.

Этапы формирования новых знаний и умений

Переходим к следующему этапу нашего плана.

Откройте задачник на странице 70. Выполним № 13.2 а,б.

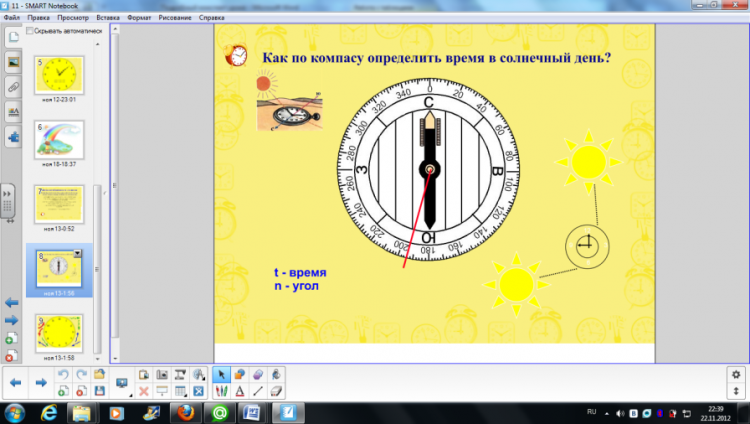
Два ученика выполнят это задание на доске. Остальные работают самостоятельно.

2;1

2;1

Проврете свое решение и поставьте карандашом плюс, если выполнили верно.

Следующий № 13.3 а,г.

На выполнение задания у вас 3 минуты.

Обменяйтесь тетрадями с соседом по парте и выполните проверку. На выполнение проверки 3 минуты.

Записать ответы на доске.

4;-14

4;3

Оцените свою работу с помощью листа самооценки.

Умение решать системы уравнений может пригодится и в жизни.

Решим следующую задачу. Как по компасу определить время в солнечный день?

Посмотрите на слайд. Здесь изображен компас с азимутальными делениями.

Известно ли вам, для чего он необходим?

Для определения угла отклонения магнитной стрелки.

По поясному декретному времени Солнце находится на юге в 13 часов при  и на востоке в 7 часов утра при .

Задача получила математическую формулировку. Найти линейную функцию  при условиях

Составим систему двух уравнений, учитывая данные условия.

Решим данную систему.

Определите t.

14 часов.

Информация о домашнем задании

Дома вам необходимо выполнить

на 3

№ 13.1 в,

№ 13.2 в,

на 4

№ 13.1 в,

№ 13.2 в,

№ 13.3 б,

на 5

№ 13.1 в,

№ 13.2 в,

№ 13.3 б, в,

чтобы отработать алгоритм решения систем двух уравнений методом алгебраического сложения.

Подведение итогов урока

Возьмите листы самооценки, посмотрите, какие этапы урока были нами пройдены, как вы справились с каждым этапом. Посчитайте количество баллов и оцените свою работу.

Посмотрите на наш план. Со всеми ли пунктами нам удалось справится?

Что нам помогало при решении систем?

Важно запомнить все шаги данного алгоритма, чтобы уметь решать системы двух уравнений методом алгебраического сложения.

Передайте листы самооценки.

Рефлексия деятельности на уроке (мероприятии, занятии)

А теперь, ребята, я вас попрошу выразить свое эмоциональное состояние. На доске изображен будильник, но он без стрелок. Имеется набор стрелок трех цветов. Красные, зеленые и синие.

Если вы считаете, что наше время не потрачено даром, вам все понравилось, вы узнали для себя что-то новое, то поместите на его циферблат красную стрелку.

Если остались вопросы, на которые вы не получили ответы, то - зеленую стрелку.

Если вы ничего не поняли и уходите с урока с плохим настроением, то - синюю стрелку.

Спасибо за работу на уроке.

В помощь учителю

Обоснование, почему данную тему оптимально изучать с использованием медиа-, мультимедиа, каким образом осуществить

Наглядное представление информации вызывает особый интерес у учащихся.

Советы по логическому переходу от данного урока к последующим

На последующих уроках имеет смысл возвращаться к алгоритму решения двух систем методом алгебраического сложения.

Другое

-