Обучение математике, как правило, сводится к тому, что ребенка знакомят с определениями, правилами и формулами. Он решает типовые задачки, суть которых в том, чтобы в нужном месте применить нужный алгоритм. Развитие мышления происходит только у небольшой части детей, обладающих задатками для изучения математики. Большая же часть учеников просто заучивает формулировки и алгоритмы действий. При этом развивается память, но не мышление. В случае, когда задание сформулировано нестандартно, учащиеся испытывают большие затруднения в его решении. С этим мы сталкиваемся при сдаче ГИА и ЕГЭ, когда ребята на вопрос, почему не справились с тем или иным заданием, отвечают «мы такого не решали», т.е. не умеют распознавать модифицированные задачи.
Сегодняшнее, информационное общество запрашивает человека обучаемого, способного самостоятельно учиться и многократно переучиваться в течение жизни, готового к самостоятельным действиям и принятию решений.
Большинство ученых признают, что развитие творческих и интеллектуальных способностей невозможно без проблемного обучения. Только через преодоление трудностей, через решение проблем ребенок может войти в мир творчества.
Я опишу несколько приёмов создания проблемных ситуаций на уроках математики. Поскольку я в этом году преподаю математику в двух 5-х классах, то мне эта тема весьма близка.
Проблемную ситуацию создают задачи с недостающими данными. Учащимся ставятся вопросы: почему нельзя дать точного ответа на вопрос задачи? Чего не хватает? Что нужно добавить? Задача. Вычислить сторону прямоугольника, имеющего площадь 24 см². Дополните условие так, чтобы задачу можно было решить однозначно. (Надо знать величину одной из сторон или отношение величин сторон).
Вторая возможность постановки учебной проблемы – подводящий диалог. Через вопросы и задания учитель подводит учеников к формулировке темы урока. В ходе беседы даются репродуктивные задания (вспомнив, выполним знакомое), и мыслительные задания (сравним, проанализируем). А последний вопрос задаётся на обобщение, ответом на него станет формулировка темы урока.
Пример. «Сложение и вычитание обыкновенных дробей с разными знаменателями».
- Учитель: Как мы складываем и вычитаем обыкновенные дроби с одинаковыми знаменателями?
- Учащиеся формулируют правила. Решают предложенные примеры.
- Учитель предлагает сложить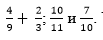 
; и . Чем отличаются от предыдущих примеров?
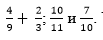; и . Чем отличаются от предыдущих примеров?- Знаменатели разные.
- Над чем на уроке будем работать?
- Сложение и вычитание обыкновенных дробей с разными знаменателями. Тема урока сформулирована.
- Как же сложить дроби с разными знаменателями? Какие есть гипотезы?
- Привести дроби к одинаковому знаменателю. (Формулируют правило, новое знание получено).
Ещё приём создания проблемной ситуации: столкновение мнений учащихся. Перед изучением темы «Сложение десятичных дробей» учащимся предлагается решить задачу: «Сколько нужно купить ленты, если на отделку юбки необходимо 13,5 метра, а для пояса - 1,83 метра ленты?»
Ученики предлагают варианты ответа, учитель записывает их на доске (среди них есть как верный, так и неверные). Далее задаёт ребятам вопросы:
- Задание было одно?
- Одно.
- А какие получились результаты?
- Разные.
- Как вы думаете, почему?
- Один из вариантов ответа: «Возможно, мы чего-то ещё не знаем».
- Какова же цель нашей работы на уроке?
- Узнать, как сложить десятичные дроби.
В результате создания проблемной ситуации и ведения проблемного диалога, учащиеся сами сформулировали образовательную цель урока. Таким образом, ребята приобретают навыки целеполагания и планирования дальнейшей деятельности.
Очередной приём создания проблемной ситуации – «ситуация предположения». Можно выдвинуть предположение о сумме внутренних углов треугольника. Уместным будет и провокационный вопрос: «В каком треугольнике сумма внутренних углов больше – в остроугольном или тупоугольном?», и проверить предположение на практике.
Следующий приём: «ситуация конфликта». Тема: «Степень числа. Квадрат и куб числа».
В начале урока предлагается знакомая ситуация: Как короче записать примеры: 3+3+3+3+3. Ученики отвечают: 3*5. Вопрос: А такой пример: 5+5+5? Ответ: 5*3. Проверьте результаты. Они одинаковы.
Учащимся предлагаются примеры: 3*3*3*3*3; 5*5*5. Как можно записать эти примеры короче? Предлагаются различные варианты ответа, чаще всего это: 3*5 и 5*3. Вычисляем: 3*3*3*3*3=81, а 3*5=15; 5*5*5=125, а 5*3=15. Осознают противоречие, фиксируют незнание: мы не знаем, как короче записывать произведение, содержащее несколько одинаковых множителей.
К проблемным ситуациям относится также приём сообщения темы с мотивирующим приёмом. Тема «Угол».
Сегодня мы познакомимся с фигурой, но какой – вы догадаетесь сами. Я буду предлагать вам вопросы, а вы попытаетесь на них ответить одним словом. Первые буквы слов и образуют тему урока.
- Какими единицами моряки измеряют скорость? (узлами)
- Старинная монета, равная половине копейки? (грош)
- Как называют прямую линию, соединяющую две точки? (отрезок)
- Расстояние от концов пальцев до локтя согнутой руки? (локоть)
- Какое слово я загадала? (Угол)
- Значит, тема урока? Угол!
Чаще всего проблемная ситуация возникает в начале урока перед объяснением нового материала.
В заключение немного рефлексии. Из опроса, проведённого среди 5-классников, следует, что ребятам нравятся уроки, на которых они сами добывают знания, проводя мини-исследования, эксперименты, выдвигая гипотезы и проверяя их.
Для учителя подготовка к таким урокам, несомненно, более трудоёмка, нежели к уроку в традиционной форме. Элементы проблемного обучения возможны только в том случае, если у учителя с ребятами установлен психологический контакт, если ученики могут переключаться с одного вида деятельности на другой, и если проблемный урок не превращается в урок хаоса и беспорядка.
Подводя итог вышесказанному, могу сделать вывод о том, что проблемное обучение приучает учащихся сталкиваться с противоречиями, разбираться в них, искать решение, а потому является одним из средств формирования диалектического мышления, т.е. является универсальным учебным действием, что позволяет достичь метапредметных результатов, т.е. таких способов действия, когда учащиеся могут принимать решения не только в рамках заданного учебного процесса, но и в рамках различных жизненных ситуаций. А именно это важно сегодня, когда от современного выпускника школы требуются мобильность, креативность, способность находить и применять свои знания на практике, умение мыслить нестандартно.