Муниципальное бюджетное общеобразовательное учреждение- средняя общеобразовательная школа №37 имени дважды Героя Советского Союза М.Е.Катукова г. Орла
Цели урока:
1.Обобщение и систематизация знаний и умений учащихся по данной теме, решение задач с использованием свойств четырехугольников.
2. Развитие умений учащихся комплексного использования полученных знаний, применение их при моделировании фигур и решении нестандартных задач.
3. Использование различных видов деятельности на уроке, развитие умений быстро переключать внимание, сосредотачиваться на определенной работе.
Планируемые результаты урока.
Метапредметные: уметь сравнивать, анализировать и классифицировать группы четырехугольников по их признакам.
Предметные: 1) знать определение всех видов четырехугольников; 2) уметь применять свойства для решения задач.
1. Организационный момент.
Вступительное слово учителя. Тема нашего урока – «Четырехугольники», на котором мы повторим полученные теоретические знания и закрепим их применение при решении задач. Эпиграфом к нашему уроку будут слова
Г. Галилея: «Геометрия дает нам возможность правильно мыслить и рассуждать.»
2. Актуализация опорных знаний.
Проверка усвоения теоретического материала.
Применяя свойства фигур, ответьте на следующие вопросы:
1.У какой из фигур диагонали пересекаясь, делятся пополам?
(параллелограмм, прямоугольник, ромб, квадрат)
2. У какой из фигур диагонали равны?
(прямоугольник, квадрат)
3. У какой из фигур диагонали делят углы пополам?
(ромб, квадрат)
4. У какой из фигур диагонали перпендикулярны?
(ромб, квадрат)
5. У какой из фигур диагонали равны и перпендикулярны?
(квадрат)
6. У какой из фигур противоположные углы равны?
(параллелограмм, прямоугольник, ромб, квадрат)
7. У какой из фигур равны все углы?
(прямоугольник квадрат)
8. У какой из фигур противолежащие стороны попарно равны?
(параллелограмм, прямоугольник, ромб, квадрат)
9. У какой из фигур только одна пара противолежащих сторон параллельна? (трапеция).
Дальше предлагается повторить признаки четырехугольников. Учащимся предлагается сформулировать теоремы, выражающие признаки параллелограмма, прямоугольника и ромба.
Решаем задачи с практическим содержанием:
№1. Школьная мастерская изготовила партию пластин, четырехугольной формы. Как проверить, будут ли пластины иметь форму прямоугольника, располагая лишь линейкой с делениями?
(диагонали равны)
№ 2. Как плотник может отпилить край доски под углом 45°?
(у квадрата диагонали образуют со стороной угол 45)
№ 3. Паркетчик, проверяя, имеет ли выпиленный четырехугольник форму квадрата, убеждается, что диагонали равны и пересекаются под прямым углом. Достаточна ли такая проверка?
(да, квадрат)
№ 4. Для того, чтобы убедиться, имеет ли четырехугольный кусок ткани форму квадрата, этот кусок дважды перегибают сначала по одной, а затем по другой диагонали. Образующиеся треугольники оба раза точно совмещаются. Можно ли утверждать, что подобная проверка показывает, что этот кусок ткани действительно имеет форму квадрата? (нет, может быть ромб)
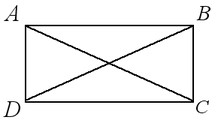
Дано: АВСD – прямоугольник,
АС = 28 см,
АС∩ВD = О,
АОВ = 1200.
Найти: ВС.
Решение:
1. (смежные углы).
2. ∆ВОС – равнобедренный, ВО = ОС = 14см (по свойству диагоналей), значит , следовательно ∆ВОС – равносторонний и
ВС = 14 см.
Ответ: 14 см.
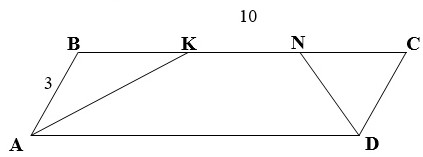
Дано: ABCD – параллелограмм
AB = 3 см, BC = 10 см
AK и DN – биссектрисы
Найти: BK, KN, NC
Решение:
|ABK-равнобедренный, AB = BK = 3 см (AK – биссектриса)
|DCN-равнобедренный, CD = CN = 3 см (DN – биссектриса)
BC = BK + KN + NC
3 + 3 + KN = BC
6 + KN = 10, KN = 4 см
Ответ: 3 см, 4 см, 3 см.
4. Тест :
|
Вопросы, I вариант |
Ответы |
|
1. Любой прямоугольник является … |
а) Ромбом |
|
2. Если в четырехугольнике диагонали равны, |
а) Ромб |
|
3. Ромб, у которого один угол прямой является |
а) Квадратом |
|
4. Какой четырехугольник не имеет собственно свойств, |
а) Прямоугольник |
|
5. Если в параллелограмме диагонали равны, |
а) Ромб |
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Тест :
|
Вопросы, II вариант |
Ответы |
|
1. Любой квадрат является … |
а) Параллелограммом |
|
2. Если в параллелограмме диагонали перпендикулярны, |
а) Ромб |
|
3. В ромбе… |
а) Все углы равны |
|
4. Параллелограмм, один из углов которого прямой является… |
а) Прямоугольником |
|
5. Если в четырехугольнике диагонали перпендикулярны, |
а) Ромб |
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Предлагается заслушать сказку, которая заканчивается тремя вопросами. Прослушав сказку (2 р) ответьте на вопросы.
Сказка-вопрос
Собрались все четырехугольники на одной поляне и стали обсуждать вопрос о выборе своего короля. Долго спорили и никак не могли придти к единому мнению. И вот один старый параллелограмм сказал: «Давайте отправимся в царство четырехугольников. Кто первый придет, тот и будет королем». Все согласились. Рано утром отправились все в далекое путешествие. На их пути встретилась глубокая река, которая сказала: «Переплывут меня только те, у кого диагонали пересекаются и точкой пересечения делятся пополам». Часть четырехугольников осталась на берегу, остальные благополучно переплыли реку и отправились дальше. На пути им встретилась высокая гора, котораясказала, что даст пройти только тем, у кого диагонали равны. Несколько путешественников остались у горы, остальные продолжили путь. Они дошли до большого обрыва, где был узкий мост. Мост сказал, что пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошел только один четырехугольник, который первым добрался до царства и был провозглашен королем.
Вопросы:
1) Кто стал королем?
2) Кто был основным соперником?
3) Кто первым выбыл из соревнования?
7. Задание на дом. П 42 – 46 (повторить) №407, 428.
|
1.На уроке я работал |
Активно \ пассивно |
|
2.Своей работой на уроке я |
Доволен \ не доволен |
|
3.Урок для меня показался |
Коротким \ длинным |
|
4.За урок я |
Не устал \ устал |
|
5.Моё настроение |
Стало лучше \ стало хуже |
|
6.Материал урока мне был |
Понятен \ не понятен Полезен \ не полезен Интересен \ скучен |
|
7.Домашнее задание мне кажется |
Лёгким \ трудным Интересно \ не интересно |
