В настоящее время общеобразовательная школа выступает в качестве того общественного учреждения, которое самым непосредственным образом отвечает за интеллектуальные ресурсы общества. И от того, как будет функционировать школа, зависят не только настоящие, но и будущие условия жизни людей [1].
В условиях современной школы творческий потенциал учащегося имеет хорошие задатки для своего развития, но при построении современной системы образования факторов для эффективного развития данных задатков недостаточно. Математика начинается вовсе не со счета, что кажется очевидным, а с …загадки, проблемы. Чтобы у школьника развивалось творческое мышление, необходимо, чтобы он почувствовал удивление и любопытство, повторил путь человечества в познании, удовлетворил возникшие потребности. Только через преодоление трудностей, решение проблем, ребёнок может войти в мир творчества.
Многолетний опыт показывает, что развитие творческого потенциала школьников на уроках математики будет эффективным, если:
- модифицировать учебную программу и осуществлять учебный процесс в соответствии с познавательными способностями ребёнка;
- делать акцент не столько на формировании знаний, сколько на развитии навыков, позволяющих самостоятельно пополнять знания, ориентироваться в потоке информации;
- строить обучение каждого ребёнка в соответствии с результатами диагностического обследования и развивать учащегося с уже достигнутого им уровня, учитывая индивидуальные способности;
- обеспечивать богатство содержания обучения и многообразие видов деятельности на уроке;
- создавать условия для конкретного воплощения творческих идей, предоставлять ребёнку свободу выбора области приложения сил и методов достижения цели; уметь воздерживаться от вмешательства в процесс творческой деятельности;
- на уроках уделять внимание развитию дивергентного мышления, характеризующегося быстротой, гибкостью, оригинальностью и точностью, охватом всех возможностей, порождением оригинальных идей в ситуации успеха, увлечённости и удовлетворенности детей учением;
- помогать ребёнку открывать и ценить в себе творческую личность.
Необходимость готовить к творчеству каждого растущего человека не нуждается в доказательствах. Именно на это должны быть направлены усилия педагогов.
Именно на уроках геометрии формируются различные универсальные учебные действия, которые способствуют развитию интеллектуальной активности личности, способной к поисковой и исследовательской деятельности, творческой самореализации, развитию творческого мышления.
Построение же и внедрение системы обучения НФТМ-ТРИЗ, отвечающей требованиям современного социального запроса, даст возможность сформировать гармонично развитую личность, с высоким уровнем творческого потенциала.
Предлагаю урок на развитие творческих способностей учащихся.
Разработка урока в 8 классе по теме «Площадь прямоугольника, параллелограмма, треугольника, трапеции».
Цель урока:
- формировать способность к исследовательской деятельности учащихся, вывести формулы для вычисления площадей прямоугольника параллелограмма, треугольника и трапеции;
- показать применение формул в процессе решения задач;
Ход урока
1. Мотивация.
Выпишите последовательно цифры 1, 2, 3, 4, 5, 6, 7, 8, 9. Сложите в уме любые три цифры, следующие одна за другой. И назовите результат. После чего я сразу же назову задуманное вами число.
2. Содержательная часть [2].
ВТ (взаимотренаж)
Карточка №1
- Понятие площади. Что означает найти площадь.
- Сформулируй основные свойства площади.
- Сформулируй признаки равенства треугольников.
- Назови единицы измерения площади.
- Сторона квадрата равна 9 см. Может ли его площадь выражаться следующим числом:
А) 35 Б) 36 В) 81
Карточка № 2
1. Чему равна площадь квадрата?
2. Сформулируй основные свойства площадей.
3. Сформулируй, чему равен квадрат двучлена?
4. Назовите единицы измерения площадей.
5. Площадь квадрата равна 121 кв. см., может ли сторона выражаться следующим числом
А) 15 Б) 11 В) 34
Работа в МГ (малые группы) [3].
Задание: Поле, имеющее форму рис.1. нужно засеять пшеницей. Норма высева на 1 га – 2 ц. зерна
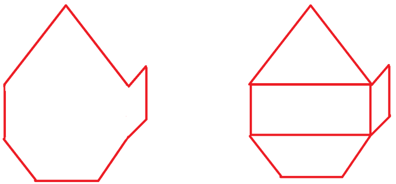
Рис.1.
В ходе работы учащиеся предлагают разбить данную фигуру на квадрат, прямоугольник, трапецию, треугольник и параллелограмм. Делают вывод, что на уроке мы будем выводить формулы этих площадей. Учащиеся формулируют тему урока и его цель.
В ходе работы учащиеся предлагают разбить данную фигуру на квадрат, прямоугольник, трапецию, треугольник и параллелограмм. Делают вывод, что на уроке мы будем выводить формулы этих площадей. Учащиеся формулируют тему урока и его цель.
Тема урока: Формулы площадей прямоугольника, параллелограмма, треугольника и трапеции.
Работа в МГ Метод «мозговой штурм» [2].
1. Вывод формулы площади прямоугольника.
Для этого давайте определим связи между прямоугольником и квадратом и установим в чём их противоречие (Таблица 1) [4].
Таблица 1
|
Фигура |
Сходства |
Различие |
|
прямоугольник |
- все углы прямые - противоположные стороны параллельны и равны - четырехугольник |
- смежные стороны не равны. |
|
квадрат |
- все углы прямые - противоположные стороны параллельны, - четырехугольник |
- смежные стороны равны. |
Вывод учащихся:
Если исключить противоречие, то можно сделать вывод, что квадрат частный случай прямоугольника. Выдвигают гипотезу, что площадь прямоугольника равна произведению смежных сторон [4].
Работа в ППС (пары постоянного состава) [3].
Учащиеся убеждаются в правильности своего вывода.
Читают доказательство этой гипотезы в учебнике стр.122 [5].
2. Вывод формулы площади параллелограмма
Работа в МГ (малых группах) [3].
Для этого определяют связи между прямоугольником и параллелограммом и устанавливают, в чем их противоречие (Таблица 2) [6].
Таблица 2
|
Фигура |
Сходства |
Различие |
|
прямоугольник |
- противоположные стороны параллельны и равны - четырехугольник |
- углы прямые |
|
параллелограмм |
- противоположные стороны параллельны и равны, - четырехугольник |
- углы не прямые |
Вывод учащихся: Прямоугольник частный случай параллелограмма, когда смежная сторона не перпендикулярна, следовательно, нужно построить этот перпендикуляр и выдвигают гипотезу, что площадь параллелограмма равна произведению его основания на высоту.
Работа в ППС [3].
Убеждаются в правильности своей гипотезы, читая текст учебника стр.123 [5].
3. Вывод формулы площади треугольника [6].
Работа в парах ППС [3].
С помощью моделей параллелограмма и ножниц попробуйте самостоятельно вывести формулу для вычисления площади треугольника.
Работа в ППС [3].
Убеждаемся в правильности своих выводов, читая текст учебника стр. 125 [5].
3. Психологическая разгрузка.
- массаж волосистой части головы: левая рука работает с правой частью головы, а правая с левой. Начать с поглаживания, затем – растирание, т.е. более интенсивные поглаживания, затем – разминание, т.е. сдвигание кожи, закончить опять поглаживанием. Делать движения как радиальные (от макушки или к макушке), так и поперечные.
- массаж ушей: оттянуть вниз мочки ушных раковин; потянуть вверх верхушки ушей; взявшись за середину ушей, оттянуть их вперед, назад и в стороны.
- массаж щёк: указательными и средними пальцами обеих рук одновременно «рисовать» сходящиеся и расходящиеся круги по контуру щёк.
- массаж лба и подбородка; указательными и средними пальцами обеих рук одновременно «рисовать» круги по контуру лба и на подбородке. Движения выполнять в противоположных направлениях.
- массаж век: указательными и средними пальцами обеих рук «рисовать» вокруг глаз очки (глаза открыты). Движения от медиальных концов бровей по глазницам до внутренних углов глаз.
- массаж носа: подушечками указательных пальцев обеих рук сильно нажимать на следующие точки: на переносице на уровне внутренних углов глаз; на середине носовой кости; у края носовой кости (над ноздрей); под ноздрей (чтобы сила надавливания была достаточной, локти следует развести в стороны, руки параллельны полу).
4. Головоломки.
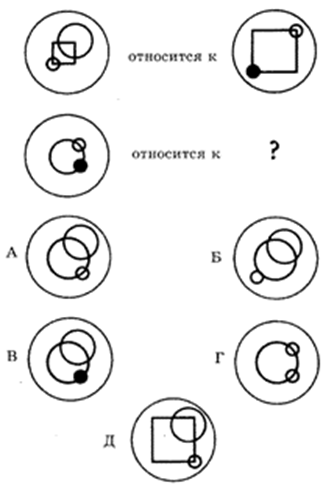
Рис. 2.
Какая из фигур должна стоять на месте знака «?» (Рис. 2.).
5. Содержательная часть
4. Вывод формулы площади трапеции.
Перед вами трапеция. Как, используя полученные знания, вывести формулу площади трапеции?
Рис. 3.
Учащиеся выдвигают гипотезу и доказывают её.
Работа в парах (ППС)
Читают текст учебника стр. 127.
Учитель:
Теперь достаточно наших знаний, чтобы определить площадь поля и количества зерна?
Продолжают работать в ППС. Высчитываю количества зерна.
Работа в ППС. Взаимопроверка.
Решение задачи № 461, № 464
6. КИП
С помощью компьютерной программы выполните следующее задание.
Творческая работа
Из треугольников составить: квадрат площадью 16 кв. см,
прямоугольник – площадью 32 кв. см,
квадрат – площадью 64 кв. см,
параллелограмм – с площадью 48 кв. см.
трапецию – площадью 48 кв. см.
Домашнее задание.
Вы купили некондиционную плитку в виде равностороннего треугольника заданного размера.
1 группа: выложить тротуарную дорожку длиной 8м и шириной 80 см, если цена одной плитки 18 рублей и размер 20*20 см.
2 группа: выложить полы на кухне длиной 4м и шириной 3,5 м, если цена одной плитки 30 рублей и размер 30*30 см.
3 группа: выложить стену в ванной шириной 2,5 м и высотой 2 м, если цена одной плитки 45 рублей, размер 25*25 см. Рассчитайте, какое количество плитки потребуется, сколько рублей придется заплатить?
7. Блок (резюме)
Приём рефлексии.
«Аргументация своего ответа»
Учащимся даётся индивидуальная карточка, в которой нужно подчеркнуть фразы, характеризующие работу ученика на уроке по трём параметрам:
Таблица 3
|
Урок |
Я на уроке |
Итог |
|
1. Интересен. |
1. Я работал(а). |
1. Материал поняла. |
|
2. Скучно. |
2. Я отдыхал(а). |
2. Узнал(а) больше, чем знал. |
|
3. Безразлично. |
3. Помогал(а) другим. |
3. Не понял(а). |
Великий китайский мудрец Конфуций (551-479 лет до н.э.) сказал: «Скажи мне и я забуду, покажи, и я запомню. Дай мне действовать самому, и я научусь».
(Китайская мудрость)
Ссылки на источники
- Федеральный государственный образовательный стандарт основного общего образования: Федер. Закон Рос. Федерации от 17 декабря 2010 г. №1897-ФЗ
- Зиновкина М. М., Утёмов В. В. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ // Концепт. – 2013. – Современные научные исследования. Выпуск 1. – ART 53572. – URL: http://e-koncept.ru/2013/53572.htm. – Гос. рег. Эл No ФС 77-49965. – ISSN 2304-120X
- Не классно-урочное обучение: модели, содержание образования, управление: Сборник статей / Редакторы-составители В. Б. Лебединцев, О. В. Запятая, Н. М. Горленко, Г. В. Клепец. – Красноярск, 2006. – 124
- Утёмов В.В. Технология формирования креативного мышления на основе задач открытого типа. Вестник Сургутского государственного педагогического университета. 2011. № 3. С. 51-57.
- Геометрия. 7-9 класс. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. В. 2010
- Утёмов В.В. Система задач открытого типа как средство развития креативности учащихся // Современные проблемы науки и образования. – 2011. – № 5;
URL: www.science-education.ru/99-4805 (дата обращения: 29.11.2013).
Tsareva Olga,
teacher of mathematics of the Municipalstate school, Nikolsk village, Abansky region Krasnoyarsk territory.
Development of creative thinking of pupils at mathematics lessons
Abstract.The article deals with the description of a creative lesson on the formation of the universal system of continuous learning activities in math class. Presented the development of creative lessons in line with the structure of a lesson in creative innovative pedagogical system TRIZ developed all the blocks lesson. The solution of practical and creative tasks in accordance with the chosen theme.
Keywords: universal learning activities, creative tasks, creativity, formation of creative competence student.