Основные цели:
1) Сформировать умение складывать трёхзначные числа с переходом через два разряда.
2) Тренировать умения записывать сложение столбиком, соотносить единицы длины с единицами счёта, решать примеры с помощью графических моделей.
3) Сформировать умение решать задачи на одновременное движение навстречу.
Мыслительные операции, необходимые на этапе проектирования: сравнение, анализ, обобщение, аналогия.
Демонстрационный материал:
1) «Книга рекордов Гиннеса»;
2) карточки, на которых:
на обратной стороне каждой карточки написано соответствующее число: 245, 76, 168, 130;
3) фото самого высокого и самого низкого человека (если возможно):

4) опорные сигналы для распознавания примеров на сложение

трёхзначных чисел с переходом через разряд (из урока 2-1-28):
5) опорный сигнал для распознавания примеров нового типа: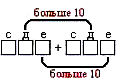

6) пособие «Треугольники и точки»;
7) эталоны сложения трехзначных чисел с переходом через один разряд (из урока 2-1-28):
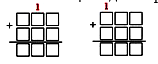
8) эталон сложения трёхзначных чисел с переходом через два разряда: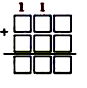

Раздаточный материал:
1) листы с заданием для пробного действия: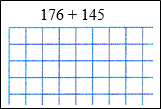

2) листы А–4 по количеству групп с заготовкой для уточнения эталона: 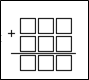

Ход урока:
1. Мотивация к учебной деятельности.
Цель:
1) создать условия для возникновения внутренней потребности включения в учебную деятельность на уроке посредством связи с темами предыдущих уроков;
2) актуализировать требования к ученику со стороны учебной деятельности;
3) установить тематические рамки урока: работа с трёхзначными числами.
Организация учебного процесса на этапе 1:
– С какими числами вы работали на последних уроках математики? (С трёхзначными.)
– Что вы умеете делать с этими числами? (Сравнивать, складывать, вычитать, …)
– Сегодня вы продолжите работу с трёхзначными числами и узнаете новое о сложении трёхзначных чисел. Скажите, а как человек может узнать что-то новое, т.е. научиться чему-то? (Надо попробовать сделать то, чего никогда не делал. Если не получится, надо подумать, почему не получилось, поставить себе цель …)
– Молодцы! С чего предлагаете начать? (С повторения необходимого.)
2. Актуализация знаний и фиксация затруднения в пробном учебном действии.
Цель:
1) тренировать умения соотносить единицы длины с единицами счёта, решать примеры на сложение трёхзначных чисел с переходом через разряд в столбик;
2) провести контроль устных вычислительных навыков учащихся;
3) активизировать мыслительные операции: сравнение, анализ, аналогию;
4) мотивировать учащихся к выполнению пробного действия;
5) организовать самостоятельное выполнение учащимися индивидуального задания на применение нового знания, запланированного для изучения на данном уроке;
6) организовать фиксацию учащимися возникшего затруднения в обосновании правильности полученного результата.
Организация учебного процесса на этапе 2:
1) Соотношение единиц измерения длины с единицами счёта.
– На уроках математики мы постоянно работаем с числами. Числа могут рассказать много интересного. Удивительные факты, связанные с числами, собраны в необычной книге – «Книге рекордов Гиннеса».
Учитель показывает книгу.
– Рекорд – это наибольший или наилучший показатель чего-либо, т.е. «самый-самый»: самый ловкий, самый быстрый и т.д. В этой книге собраны сведения о самых разных рекордах в жизни нашей планеты. В ней можно найти сведения о самых высоких и самых низких людях. Например, самым высоким жителем планеты является китаец Ван Фензель. Его рост 2 м45 см.
Повесить карточку на доску:
– Рост обычного взрослого человека – 1 м68 см.
Повесить карточку на доску: . Рядом с карточкой повесить фото.
– Самый маленький в мире человек – португалец Антонио Феррейро, рост которого в 44 года был
7 дм 6 см.
Повесить карточку на доску:
– Для того чтобы себе это представить, сравните с вашим ростом, который равен примерно 1 м30 см.
Повесить карточку на доску:
– Каждый из вас на 60-70 сантиметров выше этого человека.
– Выразите эти величины в сантиметрах и соотнесите с единицами счёта.
По одному с места устно. (2 м45 см = 245 см, соответствует числу 245. 1 м68 см = 168 см, соответствует числу 168. 7 дм 6 см = 76 см, соответствует числу 76. 1 м30 см = 130 см, соответствует числу 130.)
Учитель со слов детей переворачивает карточки, открывая ответы:
– Расположите эти числа в порядке возрастания. (76, 130, 168, 245.)
Учитель по ходу ответов передвигает карточки.
2) Сложение трёхзначных чисел с переходом через разряд в столбик
– Вы считали устно. А какой письменный приём сложения и вычитания трёхзначных чисел вы знаете? (В столбик.)
– Решите пример, записав его столбиком: 128 + 114.
Открыть запись выражения на доске.
– Каким алгоритмом воспользуетесь? Почему именно этим? (Алгоритмом сложения с переходом через разряд, т.к. при сложении единиц получится число больше 10.)
Обратить внимание детей на эталон (первый), вывешенный на стенде:
Один у доски с объяснением, остальные – в тетрадях.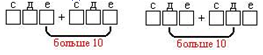

(Пишу единицы по единицами,… Складываю единицы: 8 + 4 = 12 единицам, 2 единицы пишу под единицами, 1 десяток запоминаю. Складываю десятки: 2 + 1 + 1 = 4 десяткам, 4 пишу под десятками. Складываю сотни: 1 + 1 = 2 сотням. Ответ: 242.)
По ходу ответа учитель обращает внимание детей на эталон сложения (первый) трёхзначных чисел с переходом через разряд в столбик:
– Отлично! 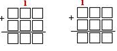 Именно знание способа сложения трёхзначных чисел с переходом через разряд будет вам сегодня необходимо.
Именно знание способа сложения трёхзначных чисел с переходом через разряд будет вам сегодня необходимо.
 Именно знание способа сложения трёхзначных чисел с переходом через разряд будет вам сегодня необходимо.
Именно знание способа сложения трёхзначных чисел с переходом через разряд будет вам сегодня необходимо.– Этап повторения завершён. Что дальше? (Надо выполнить задание для пробного действия.)
– В чём особенность задания для пробного действия? (В нём есть что-то для нас новое.)
3) Задание для пробного действия.

Раздать листы с заданием.
Открыть то же выражение на доске.
– Что нового в этом примере, постарайтесь понять в ходе выполнения. Итак, запишите пример в столбик и решите его.
На выполнение задания » 30–40 секунд.
– Проверим. Назовите ответ примера. (321; 221; 211; …)
После каждого ответа учитель задаёт вопрос: «У кого такой же ответ?» и фиксирует варианты ответов детей на доске.
– Что получилось? (Получили разные ответы.)
– Поднимите руку, кто может доказать, что решил пример 176 + 145 верно.
– Вы не подняли рук, значит, в чём ваше затруднение? (Мы не можем доказать, что верно решили пример 176 + 145.)
– И что делать? (Подумать над причиной затруднения.)
3. Выявление места и причины затруднения.
Цель:
1) создать условия для проведения учащимися анализа своих действий;
2) организовать выявление и фиксацию учащимися места и причины затруднения: нет способа сложения трёхзначных чисел с переходом через два разряда.
Организация учебного процесса на этапе 3:
– Выясним причину трудности. Какое действие, и с какими числами вы выполняли? (Сложение трёхзначных чисел.)
– Ведь вы умеете это делать. Какие виды примеров на сложение трёхзначных чисел вы умеете решать? (Без перехода через разряд. Когда при сложении единиц получается больше 10 или при сложении десятков получается больше 10.)
– А что же в этом примере было для вас новым? (В этом примере при сложении получилось больше 10 и в разряде десятков, и в разряде единиц.)
Повесить на доску опорный сигнал для распознавания нового типа примеров: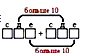

– Как в математике называют такое сложение? (Сложение с переходом через разряд.)
– Только в таком типе примеров переход не через один, а через два разряда.
– Расскажите, как вы рассуждали при решении примера на сложение трёхзначных чисел с переходом через два разряда, и было ли место в ходе ваших рассуждений, где вы засомневались. (…)
– Почему же у вас возникло затруднение в доказательстве правильности решения примера на сложение с переходом через два разряда? (Нам неизвестен способ сложения трёхзначных чисел с переходом через два разряда.)
– Причину затруднения вы зафиксировали. Что надо сделать дальше? (Надо поставить цель и выбрать средства.)
4. Построение проекта выхода из затруднения.
Цель:
1) создать условия для формулирования учащимися конкретной цели будущих учебных действий;
2) согласовать тему урока;
3) организовать выбор учащимися способа и средств для построения нового знания;
4) создать условия для составления учащимися плана дальнейших действий для достижения цели.
Организация учебного процесса на этапе 4:
– Какую цель вы перед собой поставите? (Построить способ решения примеров на сложение трёхзначных чисел с переходом через два разряда.)
– А как вы назовёте урок? (Сложение трёхзначных чисел с переходом через два разряда.)
Открыть тему на доске.
– Какие инструменты вам будут необходимы для построения нового способа? (Графические модели, способ записи и решения примеров в столбик.)
– Составьте план вашей дальнейшей работы. (Сначала решим пример с помощью графических моделей.)
Учитель последовательно фиксирует план на доске.
– Зачем вам необходимо воспользоваться графическими моделями? (Чтобы увидеть, как происходит действие.)
– Что сделаете потом? (Запишем и решим этот пример в столбик.)
Зафиксировать следующий пункт плана.
– А затем? (Сделаем вывод, построим эталон, …)
– Вы будете создавать новый эталон или будете уточнять какие-то эталоны? (Надо будет уточнить эталоны сложения трёхзначных чисел с переходом через один разряд – их надо объединить.)
Зафиксировать последний пункт плана: 3. Уточнить эталон.
5. Реализация построенного проекта.
Цель:
1) организовать построение нового способа решения примеров на сложение трёхзначных чисел с переходом через два разряда, используя предметные действия с графическими моделями;
2) организовать построение нового способа на примере, вызвавшем затруднение;
3) организовать фиксацию нового способа действий в речи и знаково путём объединения известных эталонов сложения с переходом через разряд в одном из разрядов;
4) зафиксировать преодоление возникшего ранее затруднения.
Организация учебного процесса на этапе 5:
– С чего начнёте разбираться в решении этого примера? (С составления графической модели примера.)
– Сказано – сделано.
Один ученик работает у доски, остальные – на партах: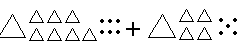
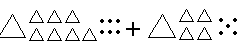
– Расскажите, как будете складывать. (Складываем сотни: 1 с + 1 с = 2 с. Складываем десятки:
7 д + 4 д = 11 д. Складываем единицы: 6 е + 5 е = 11 е. Получилось 2 с 11 д 11 е.)
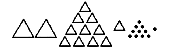
– Что делать с «лишними» десятками и единицами? (Нужно из 10 десятков образовать 1 сотню, из 10 единиц – 1 десяток.)
– Отлично, так и сделаем.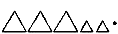
– Сколько в итоге получилось сотен, десятков, единиц? (3 с 2 д 1 е.)
– Прочитайте правильный ответ этого примера. (321.)
– Что дальше по плану? (Надо записать решение этого примера в столбик.)
– Как расположить числа, записывая решение в столбик? Почему? (Единицы под единицами, десятки под десятками, сотни под сотнями, так как удобно складывать разрядные единицы.)
– С какого разряда надо начинать сложение? Почему? (С разряда единиц, так как число десятков и сотен при переходе через разряд может изменяться.)
Один учащийся у доски с объяснением, остальные работают в тетрадях. Учитель привлекает всех учащихся к обсуждению нового способа действий при решении примера в столбик.
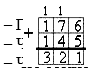
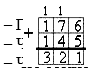
(Складываю единицы: 6 + 5 = 11 единицам, 1 единицу пишу под единицами, 1 десяток запоминаю. Складываю десятки: 7 + 4 + 1 = 12 десяткам, 2 пишу под десятками, 1 сотню запоминаю. Складываю сотни: 1 + 1 + 1 = 3 сотням. Ответ: 321.)
– Где возможна ошибка при решении таких примеров? (Можно забыть увеличить количество десятков или сотен на 1.)
– Что нужно сделать, чтобы это не забыть? (Надписать число 1 над разрядами десятков и сотен.)
– Что осталось сделать? (Осталось уточнить эталон.)
– Объединитесь в группы и уточните эталон.
Учитель руководит объединением детей в группы и раздаёт заготовки на листах А–4 каждой группе.
– Выберите представителя от группы для отчёта. Посмотрим, что у вас получилось.
Представитель от каждой группы представляет уточнённый эталон. После согласования и выступления групп лучший вариант остается на доске. В итоге эталон должен принять примерно такой вид:
– Какую цель вы перед собой ставили? 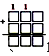 (Построить способ сложения трёхзначных чисел с переходом через два разряда.)
(Построить способ сложения трёхзначных чисел с переходом через два разряда.)
 (Построить способ сложения трёхзначных чисел с переходом через два разряда.)
(Построить способ сложения трёхзначных чисел с переходом через два разряда.)– Достигли цели? Докажите. (Мы достигли цели, так как построили способ сложения трёхзначных чисел с переходом через два разряда.)
– Этого достаточно или вам необходимо поставить перед собой ещё одну цель? (Надо научиться применять этот способ для решения примеров.)
– Итак, чем займётесь дальше? (Потренируемся в решении примеров на сложение с переходом через два разряда.)
6. Первичное закрепление с проговариванием во внешней речи.
Цель:
создать условия для выполнения учащимися нескольких типовых заданий на применение изученного способа действий с проговариванием во внешней речи.
Организация учебного процесса на этапе 6:
– Откройте № 1 (б) на стр. 56.
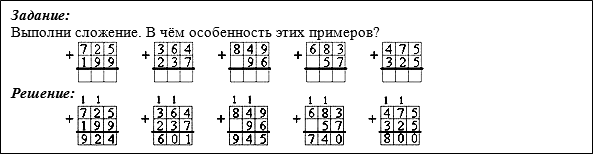

– Прочитайте задание. В чем особенность этих примеров? (Они на сложение трёхзначных чисел с переходом через два разряда.)
– Докажите, что это именно этот вид примеров. (При сложении единиц и при сложении десятков получается больше 10.)
– Решите три первых примера.
По одному у доски с объяснением, остальные – в тетрадях. (Складываю единицы: 5 + 9 = 14, 4 пишу под единицами, 1 десяток запоминаю. Складываю десятки: 2 + 9 + 1 = 12, 2 пишу под десятками, 1 сотню запоминаю. Складываю сотни: 7 + 1 + 1 = 9. Ответ: 924.)
Далее аналогично.
– Как вы можете проверить, что поняли новый способ? (Надо поработать самостоятельно.)
7. Самостоятельная работа с самопроверкой по эталону.
Цель:
1) организовать самостоятельное выполнение учащимися типовых заданий на новый способ действий;
2) организовать самопроверку учащимися своих работ по эталону для самопроверки;
3) создать (по возможности) ситуацию успеха для каждого ребёнка.
Организация учебного процесса на этапе 7:
Открыть запись на доске: 326 + 152 538 + 273 757 + 54 429 + 532.
1) – Сначала я предлагаю вам выбрать примеры на новое правило и написать карандашом на полях номера этих примеров. Какова цель этого задания? Зачем нужно различать вид примеров? (Чтобы применять соответствующий способ.)
– Что поможет при выполнении этого задания? (Опорный сигнал для выбора типа примера.)
Для выполнения работы даётся » 40 секунд.
– Проверьте себя по эталону.
Открыть на доске эталон:

– Допустили ли ошибки в выборе примеров? В чём причина? (Не сложили (сложили с ошибкой) единицы и десятки, чтобы определить тип примера)
– У кого примеры выбраны верно, поставьте на полях учебника «+».
2) – Какое задание будет следующим? (Решить эти примеры, записав их в столбик.)
– Верно. А какова цель этого задания? (Проверить, поняли ли мы способ сложения трёхзначных чисел с переходом через два разряда.)
– Запишите в тетрадь выбранные примеры в столбик и решите их.
– Проверьте.
Открыть на доске эталон: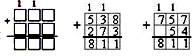

– Какие трудности возникли при решении примеров? (Неверно записали столбиком второй пример, забыли прибавить 1 десяток и 1 сотню, которую надо было запомнить, …)
– Какие правила вам надо повторить? (При записи примеров столбиком сотни пишем под сотнями, десятки – под десятками, единицы – под единицами. Чтобы не забыть прибавить один к следующему разряду, надо надписать единицу над этим разрядом.)
– У кого оба примера решены верно? Поставьте себе на полях тетради ещё один «+».
– Что интересного заметили? (Ответы обоих примеров одинаковы: 811, 811.)
– Какая здесь есть закономерность? (Закономерности нет – это просто совпадение.)
8. Включение в систему знаний и повторение.
Цель:
сформировать умение решать задачи на одновременное движение навстречу.
Организация учебного процесса на этапе 8:
– Где вам может пригодиться умение решать примеры на сложение трёхзначных чисел с переходом через два разряда? (При решении задач, уравнений, …)
– Давайте убедимся в этом, тем более что осталось время для решения задачи.
№ 2, стр. 56.

– Прочитайте условие задачи в учебнике № 2 на стр. 56.
– Как показано на чертеже, что мальчики двигаются навстречу друг другу? (Стрелками.)
– Как отмечено место встречи? (Красным флажком.)
– Выполните анализ задачи. (В задаче известно, что мальчики шли навстречу друг другу. Вадим прошёл до места встречи 342 м, а Костя – 458 м. Нужно узнать, какое расстояние было между ними вначале. Чтобы ответить на вопрос задачи, нужно к расстоянию, которое прошёл Вадим прибавить расстояние, которое прошёл Костя, т.к. ищем целое.)
– Запишите решение задачи. Как удобно это сделать? (В столбик.)
Один у доски с объяснением, остальные – в тетрадях.
9. Рефлексия учебной деятельности на уроке.
Цель:
1) организовать фиксацию учащимися степени соответствия поставленной цели и полученного результата учебной деятельности;
2) создать условия для фиксации учащимися в речи нового способа действий, изученного на уроке: сложение трёхзначных чисел с переходом через два разряда;
3) организовать фиксацию затруднений, которые остались, и способов их преодоления;
4) организовать самооценку учениками собственной учебной деятельности на уроке;
5) согласовать домашнее задание.
Организация учебного процесса на этапе 9:
– Какова была цель вашей работы на уроке? (Построить способ сложения трёхзначных чисел с переходом через два разряда.)
– Достигли цели? Докажите.
– Какие алгоритмы помогли при построении способа решения примеров нового типа? (Алгоритмы сложения трёхзначных чисел с переходом в разряде единиц и с переходом в разряде десятков)
– Какую ошибку будете стараться не допускать при решении этих примеров? (Будем стараться не забывать увеличивать количество десятков и сотен на один.)
– Когда было трудно? Удалось ли справиться с затруднениями? Как? (…)
– Кому сегодня удалось учиться по-настоящему? Почему вы так считаете? (…)
– Посмотрите ещё раз на карточки, с которых мы начали урок. Из какой книги я взяла эти числа, и что означает каждое из них?

