Формирование творческой деятельности школьников через систему внеурочной работы по математике на основе ТРИЗ

В свете Концепции модернизации образования остро встает вопрос поиска путей повышения социально-экономического потенциала общества. Это возможно в случае роста интеллектуального уровня тех, кто в дальнейшем станут носителями ведущих идей общественного процесса. Основные парадигмы развития одаренности остаются прежними: все дети одарены от природы; на развитие одаренности наибольшее влияние оказывает педагогический фактор [1].

В Национальной образовательной инициативе «Наша новая школа» говорится: «…необходимо развивать творческую среду для выявления особо одаренных ребят в каждой общеобразовательной школе…», поэтому одним из основных направлений развития общего образования является – развитие системы поддержки талантливых детей [2].

Руководствуясь положениями, изложенными в Национальной образовательной инициативе «Наша новая школа», задачами ведомственной целевой программы Томской области «Одаренные дети» на 2013–2015 годы, педагогическим коллективом МАОУ СОШ № 5 была разработана программа Межмуниципального центра по работе с одаренными детьми на территории городского округа Стрежевой и Александровского района (далее ММЦ «5+»).

Целью программы является – создание комплекса условий и средств, направленных на поддержку, развитие и социализацию одаренных детей городского округа Стрежевой и Александровского района.

Анализ проблем школьного образования усугубляет проблему недостаточности уровня сформированности инновационного мышления. С одной стороны, для формирования логичности мышления и воображения наработано немало методов и инструментов. С другой стороны, большинство выпускников школ не могут применить логику в творчестве, не могут управлять своим воображением в случае необходимости при разрешении проблемы. Проблема заключается в использовании методов обучения, не учитывающих единство и взаимосвязь элементов инновационного обучения.

Во второй половине XX века сформировалась теория решения изобретательских задач (ТРИЗ) Г. С. Альтшуллера, которую можно с большой эффективностью использовать в учебном процессе для развития элементов инновационного мышления, развития креативности учащихся.

Комплексное изучение и использование инструментов ТРИЗ в обучении в конечном итоге развивает у человека так называемое «тризовское» мышление, суть которого состоит в том, что нацеленность на идеальное решение, выявление и разрешение противоречий постепенно переходят на подсознательный уровень. Выявление и использование закономерностей развития, системный подход и другие элементы становятся неотъемлемой частью мышления, автоматически проявляясь при решении любых возникающих задач.

Система дополнительного математического образования нашей школы содержит различные компоненты, среди которых наиболее значимыми являются занятия математического кружка в различных формах, система математических соревнований, школьная математическая печать, математические игры. Все эти формы работы являются взаимопроникающими и работают на единую систему задач: привитие учащимся интереса к предмету, развитие их математического кругозора, творческих способностей, привитие навыков самостоятельной работы, что определяет в целом повышение качества математической подготовки школьников.

Высокий результат, достигнутый благодаря верно определенным и развитым способностям, будет содействовать формированию высокой самооценки, адекватной «Я-концепции» и наконец, все это вместе будет содействовать тому, что индивид принесет обществу максимум пользы [3].

Основным содержательным компонентом обозначенной системы в нашей школе, являются занятия Городской школы олимпийского резерва, к участию в которой привлекаются наиболее способные учащиеся города.

Одним из предметных направлений деятельности ММЦ «5+» является математика, руководителем которой являюсь для обучающихся 7-х и 8-х классов.

Внеурочная деятельность по математике формирует и развивает способности и личность ребёнка. Управлять этим процессом, значит, не только развивать и совершенствовать заложенное в человеке природой, но и формировать у него потребность в постоянном саморазвитии и самореализации.

Одной из важнейших целей проведения внеурочной работы по математике является развитие интереса учащихся к предмету, привлечение учащихся к занятиям в факультативах, кружках. У учащихся появляется большое желание проверить свои силы, математические способности в умении решать нестандартные задачи. Их привлекает возможность добровольного участия в данном виде творчества [4].

Внеурочная деятельность решает задачи повышения мотивации школьников к изучению математики, активизации познавательной деятельности обучающихся, развития творческого потенциала учеников. Разнообразие форм внеурочной деятельности позволяет реализовать внутренние мотивы ученика, такие как потребность в мышлении, общении, развитии интереса к математике. Это является мощным фактором развития творческого потенциала, креативности школьников.

Внеурочная деятельность объединяет все виды деятельности, в которых решаются задачи формирования универсальных учебных действий обучающихся: личностных, регулятивных, познавательных и коммуникативных [1].

Основной раздел содержит набор задач по одной из тем «нестандартной» математики: «Переливания», «Эффект плюс – минус один», «Анализ с конца», «Правила комбинаторики», «Перебор вариантов», «Четность», «Принцип Дирихле», «Правило крайнего», «Оценка + пример», «Инварианты и раскраски», «Разрезания», «Игры», «Геометрия».

1. Монету бросают трижды и записывают результат. Сколько разных последовательностей орлов и решек можно при этом получить? А если монету бросают 5 раз, 10 раз?
2. Назовем натуральное число «симпатичным», если в его записи встречаются только нечетные цифры. Сколько существует четырехзначных «симпатичных» чисел?
3. В поезде 15 вагонов. Есть 15 проводников, которые должны обслуживать каждый по одному вагону. Сколькими способами можно распределить проводников по вагонам?
4.
а) Сколькими способами 28 учеников могут выстроиться в очередь в столовую?

б) Как изменится это число, если Петю Иванова и Колю Васина нельзя ставить непосредственно друг за другом?

в) А если Петя обязательно должен стоять раньше Коли?

5. На плоскости дано n точек. Сколько имеется отрезков с концами в этих точках?
6. В США дату принято записывать так: номер месяца, потом номер дня и год. В Европе же сначала идет число, потом месяц и год. Сколько в году дней, дату которых нельзя прочитать однозначно, не зная, каким способом она написана?
7. Каких пятизначных чисел больше: не делящихся на 5 или тех, у которых ни первая, ни вторая цифра слева не пятёрка?
8. Полоска 1×10 разбита на единичные квадраты. В квадраты записывают числа 1, 2, ..., 10. Сначала в один какой-нибудь квадрат записывают число 1, затем число 2 записывают в один из соседних квадратов, затем число 3 – в один из соседних с уже занятыми и т. д. (произвольными являются выбор первого квадрата и выбор соседа на каждом шаге). Сколькими способами это можно проделать?

1. Отметьте на доске 8×8 несколько клеток так, чтобы любая (в том числе и любая отмеченная) клетка граничила по стороне ровно с одной отмеченной клеткой.
2. Можно ли из 13 кирпичей 1×1×2 сложить куб 3×3×3 с дыркой 1×1×1 в центре?
3. В левый нижний угол шахматной доски 8×8 поставлено в форме квадрата 3×3 девять фишек. Фишка может прыгать на свободное поле через рядом стоящую фишку, то есть симметрично отражаться относительно её центра (прыгать можно по вертикали, горизонтали и диагонали). Можно ли за некоторое количество таких ходов поставить все фишки вновь в форме квадрата 3×3, но в другом углу?
4. Из листа клетчатой бумаги размером 29×29 клеточек вырезали 99 квадратиков 2×2 (режут по линиям). Доказать, что из оставшейся части листа можно вырезать ещё хотя бы один такой же квадратик.

1. В классе 25 учеников. Найдется ли месяц, в котором отмечают свои дни рождения не менее трёх учеников этого класса?
2. В ковре размером 4 х 4 метра моль проела 15 дырок. Докажите, что из него можно вырезать коврик размером 1 х 1 метр, не содержащий внутри себя дырок. (Дырки считаются точечными).
3. Можно ли в клетках квадратной таблицы n´n расставить числа 1, –1, 0 так, чтобы все суммы – в каждом столбце, в каждой строке и на каждой из двух диагоналей – были различны?
4. Докажите, что среди 82 кубиков, каждый из которых выкрашен в определенный цвет, всегда можно выбрать 10 кубиков так, что либо все они выкрашены в разные цвета, либо все они одного цвета.
5. Докажите, что из любых 52 целых чисел всегда можно выбрать два, сумма или разность которых делится на 100
6. Докажите, что существует степень тройки, оканчивающаяся на 001.

1. В шахматном турнире каждый участник сыграл с каждым из остальных одну партию. Доказать, что участников можно так занумеровать, что окажется, что ни один участник не проиграл непосредственно за ним следующему.
2. Несколько прямых делят плоскость на части. Докажите, что эти части можно раскрасить в 2 цвета так, что граничащие части будут иметь разный цвет.
3. На сторонах произвольного выпуклого многоугольника снаружи растёт борода. Проводится несколько диагоналей многоугольника, так, что никакие три не пересекаются в одной точке. У каждой из этих диагоналей тоже с одной стороны растёт борода. Доказать, что хотя бы один из многоугольников, на которые разбит диагоналями исходный многоугольник, имеет бороду полностью снаружи.
4. Докажите тождества:

а) 1² + 2² +...+ n² = 1/6n(n + 1)(2n + 1)

б) 1³ + 2³ +...+ n³ = (1 + 2 +...+ n)².

5. Пусть x ≥ –1, n – натуральное число. Докажите, что (1 + x)n ≥ 1 + nx.
6. При каких n > 3 набор гирь с массами 1, 2, 3, ..., n граммов можно разложить на три равные по массе кучки?

1. На доске написано 25 букв А, 30 букв Б, 35 букв В. Разрешается стереть две разные буквы и написать третью. Такая операция проводится до тех пор, пока это возможно. Можно ли определить, какие две буквы были стерты последними?
2. На доске написаны числа 2, 6, -5, 3. За ход разрешается:

1) увеличить любое из этих чисел на 2 и уменьшить любое другое на 6,

2) увеличить любое из этих чисел на 3, увеличить любое другое на 1 и увеличить любое третье на 4.

Проделывая в любом порядке эти 2 операции (если нужно, многократно), уравняйте написанные на доске числа, или докажите, что сделать это невозможно.

3. Вася разорвал листок бумаги на 10 частей, некоторые из получившихся кусков он снова разорвал на 10 частей и т. д. Мог ли он получить 2014 кусков бумаги?
4. По окружности расставлены  натуральных чисел. Между каждыми двумя соседними числами записывают их наибольший общий делитель. После этого исходные числа стирают, а с оставшимися проделывают то же самое. Докажите, что через несколько шагов все числа станут равными.
5. В колоде часть карт лежит рубашкой вниз. Время от времени Петя вынимает из колоды пачку из одной или нескольких подряд идущих карт, в которой верхняя и нижняя карты лежат рубашкой вниз, переворачивает всю пачку как одно целое и вставляет её в то же место колоды. Докажите, что в конце концов все карты лягут рубашкой вверх, как бы ни действовал Петя.

1. На доске написано число 1. Два игрока по очереди прибавляют любое число от 1 до 5 к числу на доске и записывают вместо него сумму. Выигрывает игрок, который первый запишет на доске число 30. Укажите выигрышную стратегию для первого игрока.
2. Двое по очереди кладут монеты на круглый стол, причем так, чтобы они не накладывались друг на друга. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре? Монеты круглые, одинаковые, радиусы стола и монет не известны.
3. На окружности расставлено 20 точек. За ход разрешается соединить любые две из них отрезком, не пересекающим отрезков, проведенных ранее. Проигрывает тот, кто не может сделать ход. У кого есть выигрышная стратегия?
4. Лежит кучка в 10 миллионов спичек. Двое играют в игру. Ходят по очереди. За один ход играющий может взять из кучки спички в количестве pⁿ, где p — простое число, n = 0, 1, 2, 3,... (например, 25 спичек, 8, 1, 5, 49 и т. д.). Выигрывает тот, кто берёт последнюю спичку. Кто выигрывает при правильной игре?

Таким образом, модель дополнительных занятий по математике в совокупности с качественным основным образовательным процессом наиболее целостно реализует задачи математического образования школьников в целом. Результатом такой работы, становятся регулярные победы учащихся на олимпиадах различного уровня, значительные успехи в овладении предметом.

Одним из ключевых свойств личности для успешной жизни в современном обществе является креативность, которая проявляется и развивается в ходе решения проблемных ситуаций, а именно решения творческих задач. Отличительной особенностью реализации данного принципа является высокая степень открытости и проблемности, реализуемая посредством решения задач открытого типа [5].

Принцип ресурсного подхода предполагает широкое использование ресурсов учащихся – интересов, увлечений, желаний, потребностей и включение их в общую структуру внеурочного занятия.

Поэтому считаем необходимым в процессе развития креативности для активизации самостоятельной творческой деятельности учащихся, направленной на получение нового результата и способствующей решению задач открытого типа, использовать адаптированные инструменты ТРИЗ, предложенные Г. С. Альтшуллером в работах: «Дерзкие формулы творчества», «Правила игры без правил»:

- неалгоритмические методы активизации мышления: мозговой штурм, морфологический анализ, методы фокальных объектов, синектики и др.;

- алгоритмизированные приемы фантазирования: увеличение – уменьшение, дробление – объединение, динамизация – статика, ускорение – замедление, специализация – универсализация, оживление, «наоборот», приемы преобразования времени;

- методы, приемы и идеи ТРИЗ: системный оператор, приемы разрешения противоречий, фонды геометрических, физических и химических эффектов, метод маленьких человечков и др.

Задачи открытого типа способствуют реализации дополнительных принципов обучения, которые находятся на одном уровне с остальными (принцип свободы выбора; принцип открытости; принцип деятельности; принцип обратной связи; принцип идеальности).

Все перечисленное формирует умения предлагать оптимальные идеи, строить

эффективные рассуждения, находить оригинальные ответы, подробно описывать ход решения. Умения формируются последовательно на основе задач первого уровня открытости с постепенным включением задач более высокого уровня открытости.

Инструменты ТРИЗ используются в качестве методов решения задач открытого типа. За последние время накопился опыт разработки принципов педагогической работы [3], которые позволяют «мягко» подготовить учащихся к принятию задач открытого типа. Выделено пять принципов обучения, каждый из которых может быть раскрыт с помощью конкретных приемов, а также через задачи открытого типа.

В качестве примера представлена разработка урока математики в 5-м классе по теме «Степень числа».

1. Принцип свободы выбора. В любом обучающем или управляющем действии, где только возможно, необходимо предоставлять право выбора. С одним важным условием – право выбора всегда уравновешивается осознанной ответственностью за этот выбор. Например, предоставлять детям право выбора не только способа решения задачи, но и конкретной задачи из предложенных учителем для решения.

Задание: Вычислите значение выражений. Какие способы выполнения заданий вы нашли? Дайте характеристику каждого способа.

4+4+4+4=                                                                        4·4·4·4=

5+5+5+5+5=                                                                   5·5·5·5·5=

3+3+3+3+3+3=                                                               3·3·3·3·3·3=

2+2+2+2+2+2+2=                                                          2·2·2·2·2·2·2=

2. Принцип открытости. Необходимо не только давать знания, но еще и показывать их границы, сталкивать ученика с проблемами, решения которых лежат за пределами изучаемого курса.

Задание: Вычислите значение выражений. Что вы замечаете?

7·7

2·2·2·2·2·2·2·2

1·1·1·1·1·1·1·1·1·1·1·1·1·1·1·1·1·1·1

3. Принцип деятельности. Нужно организовать освоение учениками знаний, умений, навыков, смыслов преимущественно в форме деятельности. Чтобы знание становилось инструментом, ученик должен с ним работать.

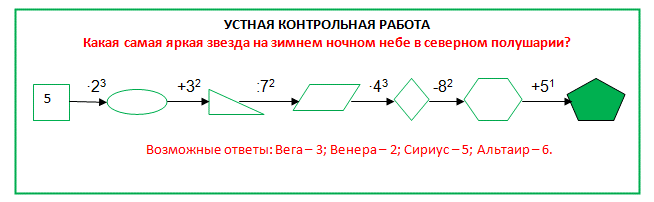
4. Принцип обратной связи. Необходимо регулярно контролировать процесс

обучения с помощью развитой системы приемов обратной связи. Чем больше развита система – техническая, экономическая, социальная или педагогическая, – тем больше в ней механизмов обратной связи.

1 вариант

2 вариант

1. Запишите в виде степени:
а) 3·3 б) 10·10·10 в) 1·1·1·1·1·1·1	а) 4·4·4 б) 2·2·2·2 в) 5·5
2.  Вычислите:
а) 53 б) 132 в) 304	а) 43 б) 122 в) 204

1. Вычислите:
а) 5·103 б) 3·22 в) (3·2)2	а) 33·10 б) 4·22 в) (2·4)2
2. Сравните числа:
а) 23 и 32 б) 42 и 32 в) 43 и 53	а) 34 и 43 б) 62 и 53 в) 34 и 24

1. Определите показатель степени числа и запишите его вместо звездочки:
а) 8* = 512 б) 2* = 64 в) 6* = 1296	а) 3* = 81 б) 7* = 343 в) 5* = 3125
2. Упростите запись, используя степень:
а) 2·2·2·5 б) (2·5)·(2·5)·(2·5) в) 13·6·6·6·6·13	а) 8·3·3 б) 17·5·5·5·17 в) (5·3)·(5·3)·(5·3)·(5·3)

5. Принцип идеальности. Идеальность – одно из ключевых понятий решения изобретательских задач. Психоаналитикам знаком принцип удовольствия, экономистам – принцип рентабельности, инженерам – принцип повышения коэффициента полезного действия. Суть всех этих принципов едина. Любое наше действие характеризуется не только получаемой от него пользой, но и затратами сил, нервов, времени и средств. Необходимо максимально использовать возможности, знания, интересы самих учащихся с целью повышения результативности и уменьшения затрат в процессе образования. Например, решая задачи открытого типа, ученик неизбежно привлекает для их решения максимальное количество имеющихся у него теоретических и практических знаний. Зачастую выбор варианта решения поставленной задачи зависит только от предпочтения самого ученика, его интереса, что, бесспорно, реализует принцип идеальности.

1. 2·2·2	а) 23 б) 8 в) 32 г) 6
2. 100·100	а) 10000 б) 100 2 в) 200 г) 2 100
3. 5·5·5·5·5·5	а) 5 6 б) 15625 в) 30 г) 65

1. 7 2	а) 49 б) 14 в) 56
2. 90 2	а) 180 б) 8100 в) 810
3. 20 3	а) 80 б) 600 в) 8000
4. 4·10 2	а) 400 б) 1600 в)160
5. 0·10 3	а) 1000 б) 0 в) 10
6. 1·10 3	а) 10 б) 100 в) 1000

1. 6·2 3	а) 48 б) 1728 в) 36
2. 27 : 3 2	а) 81 б) 3 в) 4
3. 250 : 5 3	а) 1250 б) 150 в) 2
4. (4+5) 2	а) 81 б) 18 в) 41
5. (13- 5) 2	а) 16 б) 64 в) 144
6. 10 + 5 2	а) 30 б) 35 в) 20

Таким образом, в процессе обучения на основе задач открытого типа раскрывается организационно-методическая структура процесса развития креативности, основывающаяся на концептуальных идеях личностно-деятельностного подхода. Обучение учащихся строится не только на общедидактических и частнодидактических принципах, но и на адаптированных методах и приемах ТРИЗ и принципах реализуемых на основе системы задач открытого типа [5, 6], что предполагает активное использование в учебном процессе продуктивных методов и приемов обучения. Условиями, необходимыми для развития креативности, являются создание развивающей среды, обеспечение благоприятной психологической атмосферы, воспитание учителем собственной креативности, взаимодействие педагога с родителями. Обучение, организованное таким образом, направлено на личностное развитие учащихся, повышение степени мотивации и эмоциональности, познавательной активности, творческой реализации всех участников образовательного процесса.

Задачи открытого типа предусматривают возможность применения стандартных знаний в нестандартной ситуации, при выполнении таких заданий ученик может проявить способность к логическому и абстрактному мышлению, то есть умение классифицировать, обобщать и проводить аналогии, прогнозировать результат, применяя интуицию, воображение, фантазию и, главное, способствовать развитию креативности.

Следовательно, все задачи можно разделить на учебные и внеучебные, среди них выделяются творческие задачи, которые формулируются в учебном и внеучебном процессе. Среди творческих задач выделим задачи открытого типа, которые также могут быть сформулированы как для учебного, так и для внеучебного процесса. Наглядно отношения между типами задач представлены на рисунке.
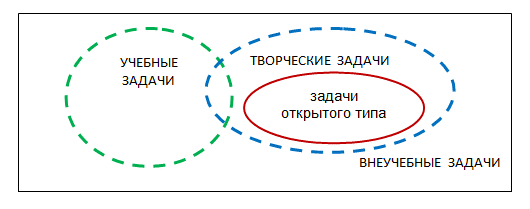Отношения между типами задач

Для развития личности учащихся необходимы не отдельные творческие задачи – задачи открытого типа, а системы творческих задач, занимающие должное место в учебной деятельности по каждой теме, в каждом школьном предмете.

Таким образом, развитие творческого креативного мышления, как учеников, так и учителей, формируется на основе системы НФТМ-ТРИЗ.