Необходимость развития творческого и креативного мышления школьников по математике, равно как и по другим дисциплинам, обусловлена социальным заказом общества и отражена в Федеральном государственном образовательном стандарте основного общего образования, утвержденном приказом № 1897 Министерства образования и науки Российской Федерации от 17 декабря 2010 года [1], указах, постановлениях, распоряжениях и иных нормативно-правовых актах по школьному образованию. Перед педагогами стоит цель развития творческих способностей и креативного мышления учащихся. В ходе работы над задачами формируется творческое мышление, пространственное воображение и изобретательность.
Урок математики в 5-м классе
Тема: «Доли. Обыкновенные дроби».
Тип урока – изучение нового материала.
Оборудование: Листы самооценки, компьютер, проектор.
Цели:
1) обучающие: знакомство с понятиями «доли», «обыкновенные дроби», «числитель», «знаменатель»; овладение навыками чтения дроби, решения задач с дробями; умение применять универсальные учебные действия:
- регулятивные: учить планировать, контролировать, оценивать свои действия;
- познавательные: учить использовать полученную информацию для решения образовательных задач
- коммуникативные: учить формулировать собственное мнение и позицию, учить сотрудничать и принимать мнения своих одноклассников.
2) воспитательные: формирование стремления к овладению ЗУН, навыков самостоятельной работы;
3) развивающие: развитие творческих способностей, пространственных представлений, интереса к предмету.
Ход урока
Учитель: На партах лежат листы самооценки [2], подпишите их и отложите в сторону. А на втором листе – незаконченное изображение. После каждого успешного выполнения задания нужно последовательно соединять точки (пятиконечная звезда).
Рис. 1Проверка домашнего задания.
Учитель: с какими трудностями вы встретились? Давайте проверим. Обменяйтесь тетрадями друг с другом (работа в парах). Оценивать будете так: 1–2 ошибки – «4», 3–4 ошибки – «3», 5 и более ошибок – «2» (презентация – слайд 1).
Рис. 2Учитель: занесите свою оценку в лист самооценки, на втором листе проведите отрезок 1–2, если у вас не менее «3».
Блок 1. Мотивация
1) Просмотр мультфильма «Апельсин» (сюжет из альманаха «Веселая карусель) – «Мы делили апельсин…».
Учитель: На сколько частей разделили апельсин? Какая часть досталась каждому?
Рис. 3
2) Актуализация знаний (устная работа – слайд 2).
Учитель: Давайте решим кроссворд и узнаем тему нашего урока.
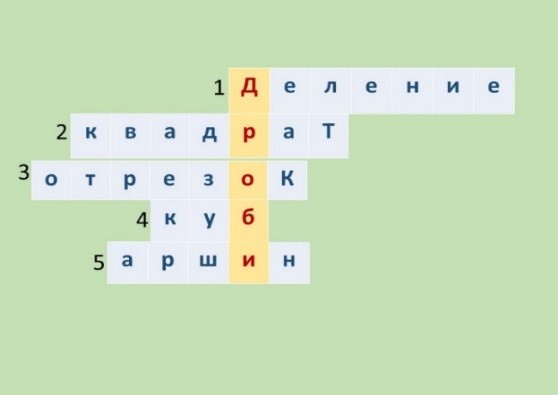
Рис. 4
Учитель: Оцените свою работу над кроссвордом, занесите в лист самооценки свой результат. Соедините отрезком точки 3 и 4.
Блок 2. Содержательная часть
Изучение нового материала (слайды 4–6).
Учитель: Какова тема урока? Запишите тему в листе самооценки.
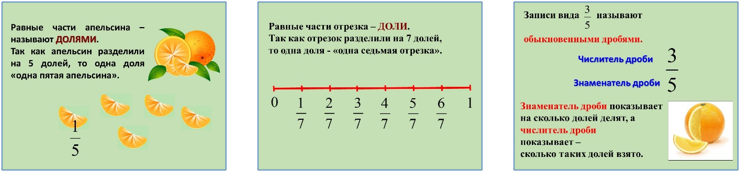
Рис. 5
Что показывает числитель? Знаменатель?
А теперь поработаем устно (слайды 7, 8).
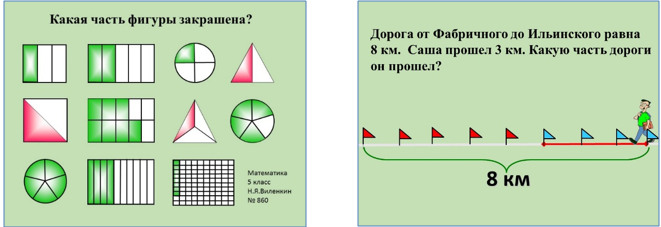
Рис. 6
Класс разбивается на группы.
Решаем задачи из учебника [3]: 1 группа – № 901, 2 группа – № 902. Проверяем.
Учитель: Кто понял, как решать задачи с дробями, дорисуйте свою звезду отрезками 4–6.
Блок 3. Психологическая разгрузка
Учитель: А теперь давайте немного отдохнем. Встаем со своих мест, начинаем суперфизкульминутку (флэш анимация) [4].
Рис. 7Блок 4. Головоломка
Учитель: С того момента, как немецкий математик Август Фердинанд Мёбиус (1790—1868) обнаружил существование удивительного одностороннего листа бумаги, начала развиваться целая новая ветвь математики, называемая топологией. Топология в основном изучает поверхности тел, и она находит математическое родство между предметами, которые, казалось бы, никак между собой не связаны.
Мы рассмотрим сейчас несколько опытов с поверхностями и отверстиями, полученными из бумажной полоски. Удобнее всего использовать полоски длиной примерно 30 см и шириной 3 см.
Чтобы получить ленту Мёбиуса, нужно повернуть полоску бумаги на пол-оборота и склеить.
Проделаем следующий опыт: не отрывая карандаша от бумаги, проведите линию по поверхности кольца.
Второй опыт: разрежьте кольцо пополам вдоль. Что получилось? Поставьте точку на одной стороне каждого кольца и чертите непрерывную линию вдоль него, пока не придете снова в отмеченную точку [5]. Какие результаты?
Учитель: Если у вас получились опыты, дорисуйте свою звезду отрезком 6–7.
Рис. 8. Лист МёбиусаБлоки 5, 7. Интеллектуальная разминка. КИП
1) Работа в группах. Класс разбивается на две команды. Два ученика – жюри. Учащимся предлагается игра «Морской бой», выполненная в виде презентации. Каждая команда называет клетку, отвечает на вопросы или пропускает ход. Жюри засчитывает баллы при правильных ответах.
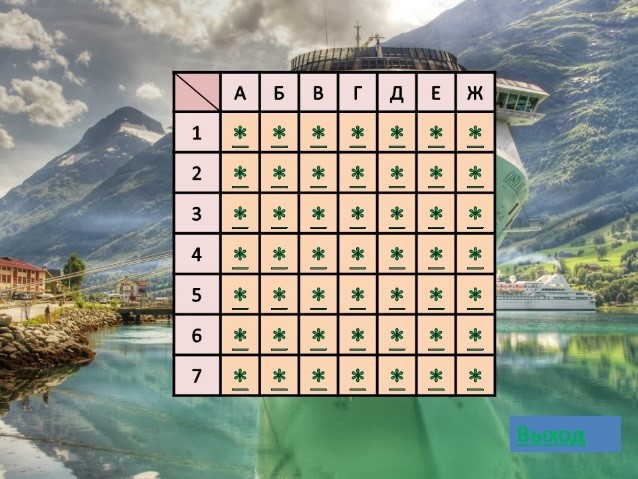Рис. 9Учитель: Оцените свою работу в команде, занесите результат в лист самооценки.
2) Самопроверка.
Учитель: Запишите через запятую пропущенные числа. Проверим. Оцените себя так:1 ошибка – «4», 2–3 ошибки – «3», 4 ошибки – «2». Занесите свою оценку в лист самооценки. Дорисуйте звезду отрезками 8 – 10.
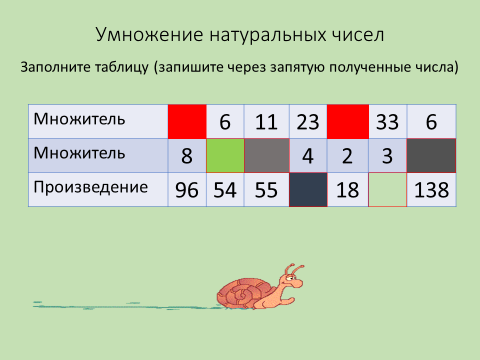
Рис. 10
3) Домашнее задание:
- п. 23 стр. 138-139, №925, 928;
- сделать лист Мёбиуса, разрезать его вдоль на три части, провести линию по поверхности, не отрывая карандаш от бумаги.
Блок 8. Резюме
Учитель: Заполните лист самооценки. На втором листе у вас должна получиться звезда. Если рисунок закончен, значит, вы продуктивно занимались на уроке, а звезда – это награда за успехи.
На доске – изображение дерева. Прикрепите тот листик, который соответствует вашим достижениям на уроке. Зеленый – мне все понравилось, я все усвоил. Желтый – некоторые задания давались мне с трудом, есть несколько ошибок. Красный – я ничего не успел, не понял (но мы тебе поможем).
Рис. 11
Оценочный лист ученика 5-го класса
_______________________________________
по теме «_______________________________»
|
№ |
Этапы урока |
оценка |
|
1 |
||
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
6 |
||
|
Итоговая оценка за урок |
||
Вопросы к кроссворду
- Арифметическая операция.
- Четырехугольник.
- Часть прямой, соединяющая две точки.
- Прямоугольный параллелепипед, у которого все измерения одинаковы.
- Старинная мера длины.
Вопросы для игры «Морской бой»
- В Московском Кремле находится Царь-пушка и Царь-колокол. Масса колокола – 200т, а масса пушки составляет массы колокола. Найдите массу пушки.
- В классе 32 ученика. из них занимаются в кружках. Сколько учеников занимаются в кружках?
- Длина маршрута 12 км. Пройдя пути, ребята сделали привал. Сколько км они прошли?
- Кусок материала разрезали на 12 равных частей. Какую долю всего куска составляет каждая часть?
- Что показывает знаменатель дроби?
- Что показывает числитель дроби?
- Какой доле кг равен 1 грамм?
- Сколько минут: а) в трети часа; б) в четверти часа; в) в шестой доле половины часа?
- После стирки кусок мыла уменьшился на 1/6 часть как по ширине, так и по высоте. На сколько таких стирок хватит оставшегося куска?
- Однажды улитка пустилась путешествовать по высокой стене: там наверху жила ее тетенька. Стена в высоту имела 10 метров. Улитка днем проползала вверх 3метра, а за ночь съезжала обратно на 2 метра. Сколько времени пришлось потратить улитке, чтобы добраться до своей тетеньки?
Процесс преподавания математики становится более креативным. Реализация программы модернизации образования в условиях сложившейся социокультурной и экономической ситуации в России при сохранении лучших традиций отечественного образования тесно связана с необходимостью осмысления новых подходов к деятельности преподавателя [4–6].
Ссылки на источники
- Федеральный государственный образовательный стандарт основного общего образования: Федер. закон Рос. Федерации от 17 декабря 2010 г. № 1897-ФЗ.
- http://aplik.ru/10-klass/listy-samootcenki (20.03.2015)
- Виленкин Н. Я. Математика 5 класс: учеб. для общеобраз. Учреждений. – М.: Мнемозина, 2008. – 280 с.
- Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: Прикладной курс научного творчества: учебное пособие. – Киров: АНОО «Межрегиональный ЦИТО», 2013. – 212 с.
- Утёмов В. В. Система задач открытого типа как средство развития креативности учащихся // Современные проблемы науки и образования. – 2011. – № 5. – С. 70
- Горев П. М., Утёмов В. В. Научное творчество: Практическое руководство по развитию креативного мышления. – М.: Книжный дом «ЛИБРОКОМ», 2013. – 112 с.