Целью обучения учащихся девятых классов является освоение обучающимися базисных основ алгебры, формирование у них высокой культуры межличностного и межэтнического общения, самоопределение личности и профессиональную ориентацию.
Но кроме этого необходимо, чтобы учащиеся на уроках отходили от стандартных решений, преодолевали инерцию в мышлении, умели работать творчески, представляя креативные решения поставленных перед ними задач.
Задачами обучения ставятся: обеспечение качественного усвоения базисных основ алгебры, направленного на воспитание и развитие интеллектуальных качеств личности: абстрактного и логического мышления, интуиции, познавательных интересов, самостоятельности, волевых качеств и др., математической речи, алгоритмической и графической культуры; развитие личности учащегося, его духовной сферы через приобщение к ценностям, накопленным математической наукой в ходе ее развития; умственное развитие учащихся через овладение индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, абстрагированием и аналогией; умением обосновывать и доказывать утверждения; развитие навыков самостоятельной работы, способности к самообразованию, самооценке при выполнении индивидуальных заданий и работе в группе; предоставление учащимся возможности самостоятельного конструирования задач по данной теме, их решения; развитие умения ориентироваться в потоке поступающей информации.
Тема: «Формулы приведения»
Целью проведения данного урока было создание условий для выработки первичных навыков у учащихся по применению формул приведение при преобразовании тригонометрических выражений.
Были определены следующие задачи
1. Образовательные:
- закрепить умение находить четверть и знак тригонометрических функций;
- закрепить умения использовать формулы сложения при упрощении тригонометрических выражений;
- вывести формулы приведения;
- выработать первичные навыки использования формул приведения;
- отработать алгоритм применения формул приведений;
2. Развивающие:
- интеллектуальное, эмоциональное, личностное развитие ученика;
- развивать умение обобщать, систематизировать на основе сравнения, делать вывод;
- активизация самостоятельной деятельности (деятельностный подход в обучении);
- развивать познавательный интерес;
- развивать наглядно-действенное творческое воображение.
3. Воспитательные:
- способствовать формированию у учащихся чувства толерантности,
- стимулировать согласованное взаимодействие между учащимися, отношения взаимной ответственности и сотрудничества.
- умение учащихся данной группы построить на короткое время взаимодействия, исходя из особенностей задач.
Предполагаемые результаты обучающихся:
Знать: формулы приведения.
Уметь: определять четверть и знак тригонометрических функций; использовать формулы сложения при упрощении тригонометрических выражений.
Форма урока: практикум, с элементами исследования.
Форма организации обучения: фронтальная, индивидуальная, групповая.
Организация работы в группах на уроке преследует следующие цели:
- научить ребят самостоятельно и правильно распределять между собой роли при выполнении общих заданий и ответственно выполнять свои обязанности;
- научить ребят быть руководителями в групповой деятельности или исполнителями, т.е. подчиняться заданным правилам совместной работы;
- научить общаться друг с другом, устанавливать и поддерживать хорошие деловые взаимоотношения;
- научить ребят умело вести дискуссию, высказываться самим и слушать других, доказывать свою правоту и признавать правильность позиций других ребят.
БЛОК 1 «МОТИВАЦИЯ»
Положительный настрой на урок:
Я это я. Во всем мире нет абсолютно такого же, как я. Мне принадлежит все, что есть во мне: сознание, мысли, чувства.
Мне принадлежат все мои фантазии, сны, мечты, желания.
Мне принадлежат мои победы и поражения, успехи и неудачи, достижения и ошибки.
Я могу видеть, слышать, чувствовать, говорить. И думать. Я могу действовать, а значит, могу жить. Я принадлежу себе и поэтому могу строить себя. И сегодня у меня есть все основания для радостной и спокойной улыбки.
Учащиеся рассажены за 4 стола (по 2 парты) группами по 6 человек в группе.
БЛОК 2 «СОДЕРЖАТЕЛЬНАЯ ЧАСТЬ»
Введение в тему урока, формирование целей.
Обращение внимания на написание слова «ПРИВЕДЕНИЯ».
- Как вы понимаете это слово? Что значит формулы приведения? (делается вывод, что какое-то более сложное выражение будем приводить к определенному более простому виду)
- Формы нашей работы сегодня: устная работа на повторение, работа в группах (сразу назначить командиров групп и рассказать, что их обязанностью является распределение составляющих общего задания между членами группы). Для того чтобы успешно справиться с работой на уроке, нам необходим материал предыдущих занятий. И первое, что нам необходимо повторить, – это тригонометрический круг, значения синуса, косинуса, тангенса и котангенса различных углов.
Разминка:
1-е задание: Тригонометрический круг – тренажер. Точка-смайлик скользит по кругу, останавливаясь то на осях координат, то на различных точках круга. Учитель называет ученика и тот быстро называет значение точки (либо угол в радианах, либо значения синуса, косинуса, тангенса или котангенса на осях).
|
|
2-е задание: Определить знак тригонометрических функций

Рис. 2
Ответы на задание № 2 «Определить знак тригонометрических функций»:
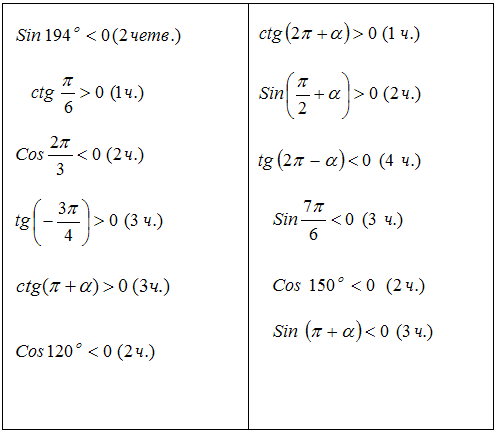
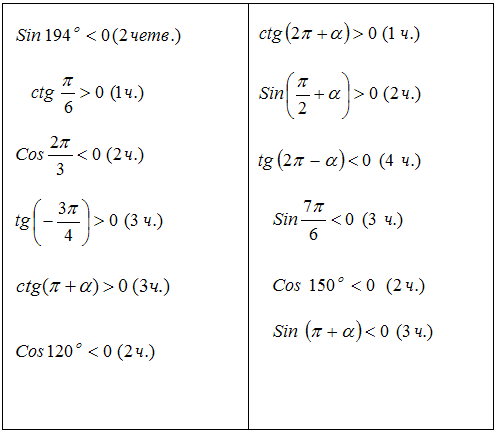
Объяснение нового материала
- Итак, мы повторили формулы сложения, которые вам сегодня еще понадобятся.
БЛОК 3 «ОТДЫХ»
Во время отдыха можно провести физкультминутку для глаз:
Исходное положение: сесть на стул, руки положить на колени, расслабиться, все внимание сосредоточить на глазах. Упражнения надо выполнять без напряжения. Дышать медленно.
Первое упражнение. На раз – поднять глаза вверх, на два – смотреть прямо, на три – потупить взор книзу, на четыре – смотреть прямо, 8 раз.
Второе упражнение. На раз – смотреть на переносицу, на два – прямо. Повторить 8 раз.
Третье упражнение. На раз – смотреть влево, на два – прямо, на три – смотреть вправо, на четыре – перед собой. Повторить 8 раз.
Четвёртое упражнение. Круговые обороты глазами – 4 раза влево, четыре вправо.
Пятое упражнение. Широко раскрыть глаза, а потом плотно закрыть. Повторить 5 раз.
БЛОК 4 «ГОЛОВОЛОМКА»
Найти как можно больше рыб на картинке.
 Рис. 3
Рис. 3ПЕРЕРЫВ
БЛОК 5 «ИНТЕЛЛЕКТУАЛЬНАЯ РАЗМИНКА»
1. Найдите зависимость: Кошке соответствует число 3, собаке число 3, корове число 2, а какое число соответствует лягушке?
2. Найдите зависимость:
2. Найдите зависимость:
ПРИТОК x > 3 ТОК
ПОСТЕЛЬ х < 5 ?
КРОТ 1 < x < 3 КОТ
КРОЛИК 2 < x < 5 ?
3. Есть две комнаты, в одной три лампочки, а в другой три выключателя, по одному для каждой лампочки. Человек находится в комнате с выключателями. Какие действия нужно произвести с выключателями, чтобы потом зайти в комнату с лампочками и точно сказать, какой выключатель управляет каждой из лампочек? Перейти из комнаты в комнату можно только один раз.
БЛОК 6 «СОДЕРЖАТЕЛЬНАЯ ЧАСТЬ»
А сейчас я вам хочу зачитать одну притчу:
Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному дверному замку. «Кто откроет, тот и будет первым помощником». Никто не притронулся даже к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ. Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься на собственные силы и не боишься сделать попытку».
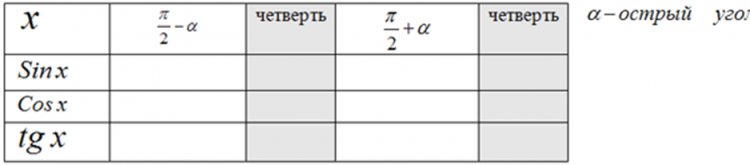
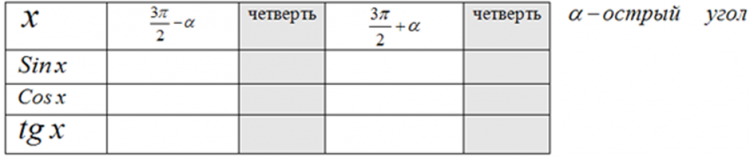
- Сейчас каждой группе предстоит сделать попытку добыть новые знания, используя предыдущий опыт, предыдущие знания. Каждой группе дается задание заполнить таблицу, используя формулы сложения. Командир разбивает задание на составляющие части и распределяет между членами группы. Работать можно прямо в тетрадях. Конечные результаты заносятся в общую таблицу, которая у вас на столе. Когда группа заполнит таблицу полностью, кто-либо из группы выносит результаты на доску. Все расчеты можно выполнять прямо в тетради. Объединив результаты работы 4-х групп, вы сами откроете и сформулируете новое правило (Дается время, на доске заготовлены 4 таблицы).
| Таблица 3-й группе |
Вопросы группам после заполнения таблицы на доске:
Что произошло с названием функции, поменялась ли функция?
Какой знак стоит перед функцией в правой полученной части?
(Группы отвечают на вопросы. Ответы фиксируются учителем).
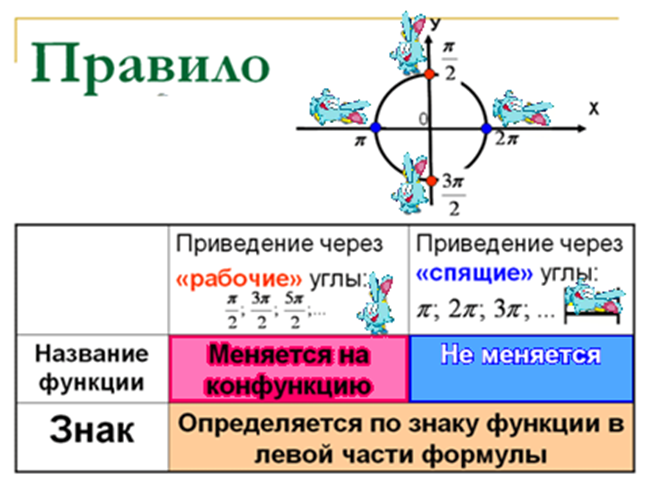
- У первой и второй группы названия функции поменялись, а у 3-й и 4-й групп остались прежними. Обратите внимание на углы, через которые вы приводили к углу 1 четверти: углы располагаются на тригонометрическом круге по вертикали, их будем называть «рабочими углами», углы располагаются на тригонометрическом круге по горизонтали, их будем называть «спящими углами». Получившийся знак перед функцией совпадает со знаком исходной функции.
- Итак, мы прослушали ответы всех групп и вывели 32 формулы. Это и есть формулы приведения. Мы приводим к функции угла 1 четверти. Сможете ли вы их запомнить? И не нужно их запоминать механически. Давайте попробуем сделать общий вывод по результатам работы всех групп и сформулируем мнемоническое правило, которое позволит вам в дальнейшем самим быстро написать все формулы, которые будут необходимо. Ключевые моменты: название функции, знак функции. Я начинаю предложение, а вы продолжаете:
Если приведение к углу выполняется через вертикальные «рабочие» углы название…. (функция меняется на конфункцию, синус на косинус, тангенс на котангенс и наоборот).
Если приведение к углу выполняется через горизонтальные «спящие» углы», то (название функции не меняется).
В правой части формулы ставится тот знак, ….. (который имеет функция левой части) или – знак правой части определяется по знаку функции в правой части.
 |
- Где же применяются формулы приведения? Одно из применений – нахождение значений тригонометрических функций различных углов с помощью приведения к углу 1-й четверти.
Например:
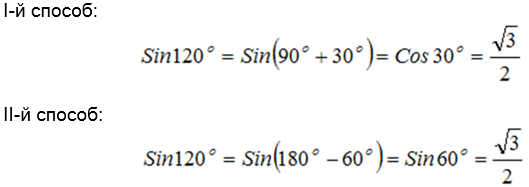
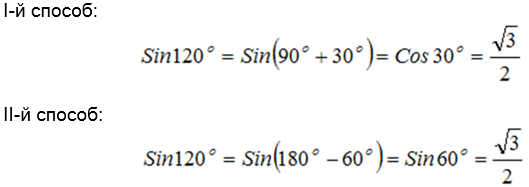
Фронтальная работа
Решение упражнений:
Тригонометрические функции от углов 120,135,150,210,240,225,300,315,330
Со слабыми учащимися № 331
Сильные учащиеся № 334; №335
Домашнее задание: правило № 330 (весь), № 333
Сильным учащимся № 336, № 337
БЛОК 7 «ИТОГ»
- Что вы сегодня узнали? (Как привести к функции угла 1 четверти)
Кто сможет повторить правило?
Но, а самый главный итог не в том, что вы узнали новое правило, а в том, что вы его вывели и получили самостоятельно. Помните притчу, которую я прочитала вам в начале урока? Так вот, главный итог в том, что вы полагались не только на то, что видели и слышали от меня, но надеялись на собственные силы и не боялись сделать попытку и получить результат самостоятельно и поэтому все замки сегодня для вас оказались открытыми.
Ссылки на источники
- Горев П.М., Утёмов В. В. Научное творчество: практическое руководство по развитию креативного мышления: Учебно-методическое пособие. – Книжный дом "ЛИБРОКОМ", 2014. – 112 с.
- Утёмов В. В. Технология формирования креативного мышления на основе задач открытого типа // Вестник Сургутского государственного педагогического университета. – 2011. – № 3. – С. 51– 57.
- Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: Прикладной курс научного творчества: Учебное пособие. - Киров: АНОО «Межрегиональный ЦИТО», 2013. – 212 с.
- Утёмов В.В. СИСТЕМА ЗАДАЧ ОТКРЫТОГО ТИПА КАК СРЕДСТВО РАЗВИТИЯ КРЕАТИВНОСТИ УЧАЩИХСЯ // Современные проблемы науки и образования. – 2011. – № 5; URL: www.science-education.ru/99-4805 (дата обращения: 08.03.2015).

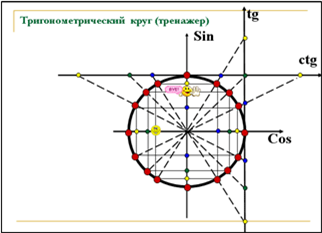 Рис. 1
Рис. 1