Использование принципов развивающего обучения при обучении школьников математике

Проблема развития учащихся при обучении является одной из центральных в современной психологии и педагогике. Исследованием этой проблемы занимались А.В. Занков, В.В.Давыдов, И.С. Якиманская, З.И.Калмыкова и др. известные педагоги и психологи.

Что же такое развивающее обучения?

Известным специалистом в области педагогической психологии И.С.Якиманской дан следующий ответ на этот вопрос: «обучение, которое, обеспечивая полноценное усвоение знаний, формирует учебную деятельность и тем самым влияет на умственное развитие, и есть развивающее обучение».[6]

В данном определении делается акцент на умственное развитие.

Что же такое умственное развитие?

Психолог З.И. Калмыкова в своей работе «Психологические принципы развивающего обучения» пишет: «Умственное развитие – сложная динамическая система количественных и качественных изменений, которые происходят в интеллектуальной деятельности человека в связи с его возрастом и обогащением жизненного опыта в соответствии с общественно-историческими условиями, в которых он живет, и с индивидуальными особенностями его психики».[2]

Она считает, что умственное развитие имеет следующую структуру:

1) Фонд действенных знаний;

2) Обучаемость;

Фонд действенных знаний имеет две стороны: содержательную, которая показывает объем знаний учащихся, и операционную, которая рассматривает приемы, способы образования понятий  школьников и умения применять их на практике.

Обучаемость – это система интеллектуальных свойств личности, формирующихся качеств ума, от которых зависит продуктивность учебной деятельности (при общих умственных способностях).

Особенности продуктивного мышления проявляются в качествах ума, последние бывают положительные и отрицательные.

Рассмотрим сначала положительные качества ума:

1) Глубина ума проявляется в степени существенности признаков, которые человек может абстрагировать при овладении новым материалом, и в уровне их обобщенности;

2) Гибкость ума проявляется в степени изменчивости мыслительной деятельности, соответствующей меняющимся условиям исследуемой ситуации, решаемой проблемы;

3) Устойчивость заключается в ориентации на совокупность выделенных ранее значимых признаков, на уже известные закономерности;

4) Осознанность мыслительной деятельности - это качество ума, позволяющее в словах выразить результат, а также способы и приемы, какими этот результат был достигнут;

5) Самостоятельность ума проявляется в активном поиске новых знаний, новых путей решения задач.

Существуют также отрицательные качества ума:

1) Поверхностность ума проявляется в выделении единичных признаков, в установлении случайных связей между ними;

2) Инертность ума проявляется в склонности к привычным ходам мыслей, в трудности переключения от одной системы действенных знаний к другой;

3) Неустойчивость заключается в трудности ориентации на признаки, входящие в содержание нового понятия  или закономерности;

4) Неосознанность мыслительной деятельности заключается в том, что ученик не может показать, как он рассуждал, как решал задачу, не замечает своих ошибок, не в состоянии указать те признаки, на которые он опирался;

5) Подражательность ума проявляется в стремлении человека копировать уже известные способы решения, избегая интеллектуального напряжения даже там, где поставленная задача ему доступна, а также к слепоте к ошибкам.
Рассмотрим на примерах, как проявляются те или иные качества ума.

1) Учащимся выданы различные четырехугольники разного цвета. И предложено как-нибудь сгруппировать полученные фигуры.

Ученики, отличающиеся глубиной ума, к одной  группе отнесут  параллелограммы, к другой – трапеции, к третьей – четырехугольники общего вида. А ученики, которые характеризуются поверхностностью ума, распределят четырехугольники по цвету.

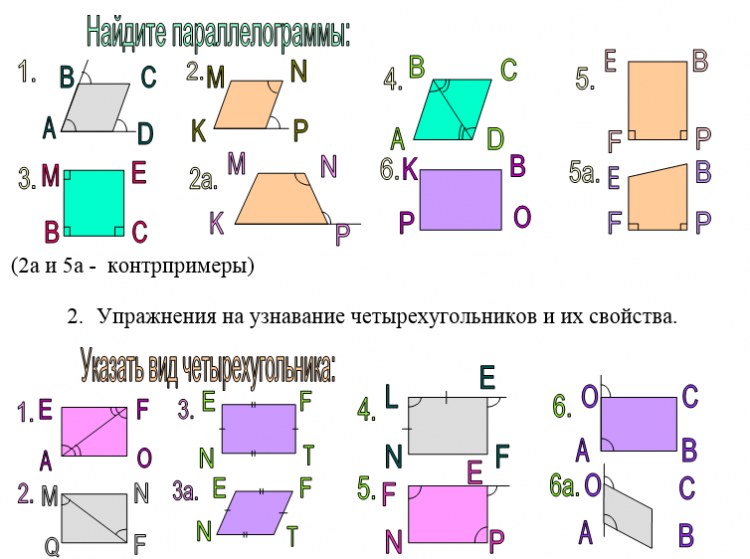
2) Ученикам дается задание: по рисункам определить вид четырехугольника.

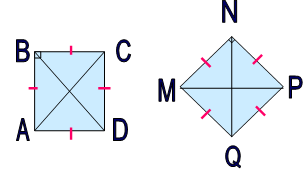Выясняется, что на первом рисунке  изображен квадрат. Предполагается определить вид четырехугольника, изображенного на  втором рисунке. Ученики, которые отличаются гибкостью ума, сразу догадаются, что это тот же самый рисунок, только развернутый. И сразу дадут ответ: на рисунке изображен квадрат. Ученики с выраженной инертностью ума будут применять те же рассуждения, что и первом случае.

3) После введения определения квадрата учащимся предложено выяснить свойства квадрата. Учащиеся с устойчивым умом используют определение квадрата и отнесут к свойствам квадрата свойства прямоугольника. А, зная, что прямоугольник – это параллелограмм, к свойствам квадрата отнесут свойства параллелограмма. У учеников с неустойчивым умом возникнут определенные проблемы с определением свойств квадрата. Это связано с неумением таких учеников использовать уже известные закономерности.

Поэтому при работе с учащимися нужно учитывать различия в качествах ума учеников. И стремиться к формированию  положительных качеств ума.

В современной дидактике существуют два основных метода обучения:

1) Наглядно-иллюстративный метод – метод, при котором материал рассказывает учитель, подтверждая свои мысли наглядно с помощью рисунков, чертежей, таблиц, моделей и т.д., используя при этом небольшие эвристики.

2) Проблемное обучение – это метод, при котором перед учащимися ставится проблема, разрешить которую учащиеся могут, лишь производя полные или частичные исследования самостоятельно или с помощью взрослых, используя при этом полученные знания и делая новые «открытия».

Проблемное обучение является одним из принципов развивающего обучения.

Важным средством создания проблемной ситуации  на уроке является задача.

Следующими принципами развивающего обучения являются:

1. Оптимальное развитии всех видов учебной деятельности.

2. Индивидуализация и дифференциация обучения.

3. Специальное формирование как алгоритмических, так и эвристических приемов.

4. Специальная организация мнемической деятельности.

Для развития учащихся необходимо пользоваться не одним принципом развивающего обучения, а всеми сразу, применяя их в системе.

Исследования показали, что школьники усваивают лишь определенный класс задач, причем довольно узкий. Необходимо специальное формирование обобщенных приемов умственной деятельности, которая делится на 2 группы:

Приемы алгоритмического типа – приемы правильного мышления, полностью соответствующие законам логики. Это приемы, позволяющие решать отдельные задачи, следуя предписаниям. Но алгоритмических приемов недостаточно для развития мышления. Необходим поиск решения задачи.

Эвристические приемы стимулируют поиск новых проблем, открытию новых знаний. К таким приемам относятся конкретизация, графический анализ, аналогии, абстрагирование, варьирование.

Значит, при обучении математики, и, в частности, при решении задач необходимо обогащать фонд действенных знаний, формируя при этом положительные качества ума и используя принципы развивающего обучения.

«Задача – это почти всегда поиск, раскрытие каких-то свойств и отношений, а средства ее решения – это интуиция и догадка, эрудиция и владения методами математики».(Б.А. Кордемский, А.А. Ахадов)

Математические задачи должны будить мысль ученика, заставлять его работать, развиваться, совершенствоваться. В этом состоит основное назначение задач и упражнений.

Задачи – проблемы – это те задачи, которые возбуждают активную мыслительную деятельность, поддерживаемую интересом, а сделанное учащимися «открытие» приносит им радость.

На примере темы «Четырехугольники» покажем, как можно применить принципы развивающего обучения при обучении школьников решению задач.

Укажем типы упражнений, необходимые при обучении решению задач:

1. Задачи, способствующие образованию и формированию понятий четырехугольник, параллелограмм, ромб, квадрат, прямоугольник, трапеция.

 

(3а и 6а -  контрпримеры)

3. Упражнения на применение признаков: найти на рисунке, объяснить.

 

 

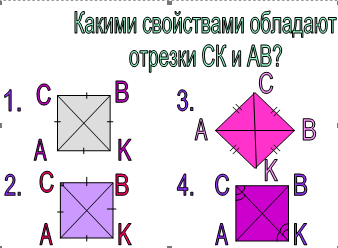
4. Упражнения на поиск недостающих условий.
5. Задачи, обучающие анализу и синтезу.      

Устные задачи:

Это задачи на узнавание свойств параллелограмма.

Задачи-вопросы:

а) Диагонали равны и взаимно перпендикулярны,

б) Диагонали взаимно перпендикулярны и имеют общую середину,

в) Диагонали равны, взаимно перпендикулярны и имеют общую середину.

5. Верно ли, что четырехугольник является ромбом тогда и только тогда, когда:

а) Его диагонали делят противоположные углы пополам,

б) Его диагонали взаимно перпендикулярны,

в) Стороны равны половине диагонали.

При решении этих задач необходимо приводить контрпримеры.

С помощью этих упражнений мы формируем положительные качества ума.

Самое главное обучить учащихся аналитико-синтетическому методу решения задач.

Для этих целей можно провести урок одной задачи:

Докажите, что четырехугольник является параллелограммом, если  и.

Решить задачу решить 3 способами.

При решении задач необходимо помнить, что задача должна быть обязательно решена.

Умение решать задачи – показатель интеллектуального развития учащихся.

И в заключении отметим, что умный ученик – это тот ученик, у которого в соответствии с его возрастом начали формироваться положительные качества ума: глубина, гибкость, устойчивость, осознанность и самостоятельность.

Литература:

1. Виноградова Л.В. Развитие мышления учащихся при обучении математике. – Петрозаводск: Карелия, 1989.

2. Калмыкова З.И. Психологические принципы развивающего обучения. – М.: Знание, 1979.

3. Костюк Г.С. Избранные психологические труды. М.: Педагогика, 1988.

4. Ланда Л.М. Умение думать. Как ему учить? – М.: Знание, 1979.

5. Метельский Н.В. Пути совершенствование обучения математике. – Минск: Университетское, 1989.

6. Якиманская И.С. Развивающее обучение. – М.: Педагогика, 1979.