Медиана, биссектриса и высота. Свойство медианы равнобедренного треугольника

Цели:
1) закрепить у уч-ся навыки применения понятий медианы, биссектрисы, высоты треугольника при решении задач;

2) познакомить уч-ся со свойствами медианы равнобедренного треугольника  и научить применять его при решении задач;

3) способствовать развитию математического мышления.

 

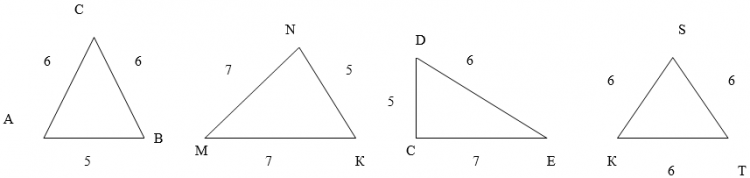
1) Какие из треугольников, изображенных на рисунке являются равнобедренными? Для равнобедренных назовите основание и боковые стороны.

  

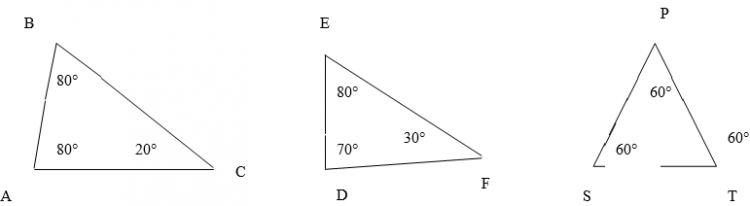
2) Треугольник АВС- равнобедренный с основанием АС;  угол А= 62° Чему равен  угол С?

3) Чему равен угол D треугольника DЕF, изображенного на рисунке:

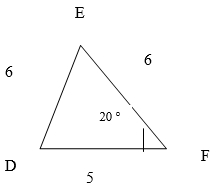4) Обоснуйте, что треугольник ADC, изображенный на рисунке, равнобедренный.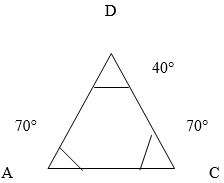

5) Какие из треугольников, изображенных на рисунке, являются равнобедренными? А какие не являются равнобедренными? Для равнобедренных треугольников назовите их основание и боковые стороны.

Работа по карточкам

III Объяснение нового материала
- Назовите, чем являются отрезки КС, LK, EF для изображенных на рисунке треугольников.

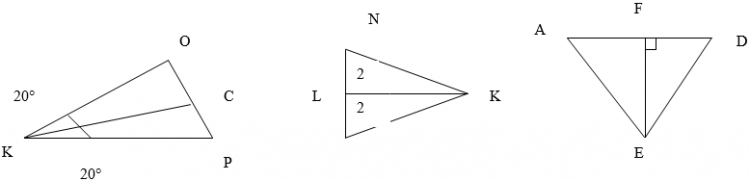
- Что называется медианой треугольника, биссектрисой, высотой?

Практическая работа

Каждый ученик получает лист, на котором изображен равнобедренный треугольник.

Задание: провести медиану к  основанию равнобедренного треугольника. Измерить углы: ACD, BCD, ADC, BDC. Что можно сказать о медиане CD?

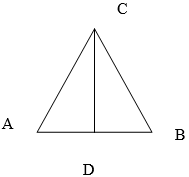Т. 3.5 Дано: треугольник ABC;  AC=DC; AD=DB.

Доказать: 1) ACD=BCD, т.е. CD- биссектриса.

2) ADC=BDC=90°, т.е. CD- высота.       

Доказательство:

1) CAD = CBD (по I пр.)

АС = ВС; АD = BD; угол А = углу В

2) Угол ACD = углу BCD => CD-биссектриса

Угол ADC = углу BDC = 90º(как смежные) => CD-высота. Ч.т.д. 

IV.Закрепление:

1) Как в равнобедренном треугольнике ОМК, с основанием ОК, провести биссектрису, высоту из вершины М, используя только линейку с делением

2) В треугольнике MNK угол М = углу К=40°, угол N=100°; NP- медиана.   

Определите стороны  треугольника MNP

3) №25 (1,2)

V. Самостоятельная работа      

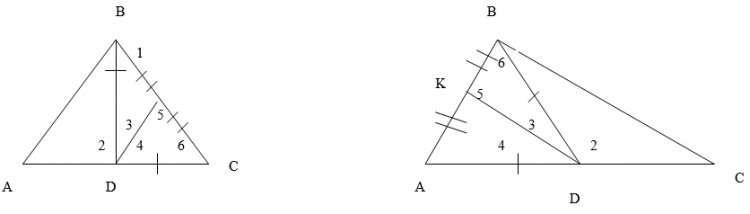
Дано: Треугольник ABC; BD = CD          Дано: треугольник  ABC,

Угол 1 = 40°; угол 2 =  80°                   AD = BD, AK = BK

Найти: угол 3, 4, 5, 6.                        Угол 1 = 50°;

                                                      угол 2 = 100°

                                                       Найти: угол 3, 4, 5, 6.
VI. Домашнее задание:
Стр. 43; в. 8-11; № 25(3); № 27.