Использование инструментов ТРИЗ на уроке математики

Необходимость развития креативной личности обуславливается социальным заказом общества и отражена в федеральных и региональных документах, например, в Федеральном государственном образовательном стандарте основного общего образования, утверждённом приказом № 1897 Министерства образования и науки Российской Федерации 17 декабря 2010 г. [1], указах, постановлениях, распоряжениях и иных нормативно-правовых актах по школьному образованию. Что же такое креативная личность, это личность обладающая творческими способностями, характеризующимися готовностью к принятию и созданию принципиально новых идей, отклоняющихся от традиционных или принятых схем мышления и входящие в структуру одарённости в качестве независимого фактора, а также способность решать проблемы, возникающие внутри статичных систем [2]. Таким образом, перед педагогами стоит задача развития творческих способностей личности. Одним из способов решения данной задачи можно рассматривать теорию решения изобретательских задач (ТРИЗ) Г. С. Альтшуллера [2].

В статье описан пример использования инструментов ТРИЗ Г. С. Альтшуллера в обучении учащихся основной школы математике для развития творческого потенциала личности. Урок обобщение по теме «Площадь прямоугольника и квадрата» в 5 классе с практической направленностью был выбран в качестве технологии проведения занятия. Структура урока отличается от традиционного и включает в себя блоки, реализующие цели занятия, адекватные целям креативного образования в целом [3]. 

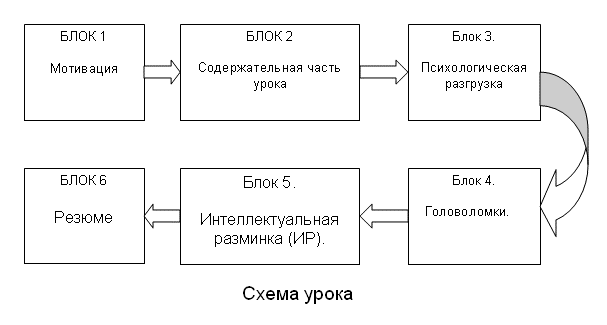
Блок 1. Мотивация (удивление, сюрприз).

«Удивление есть начало всякой мудрости» (Сократ).

С целью пробуждения поисковой активности наилучшим способом включения учеников в интеллектуальную работу является акт удивления или как его называют «эффект чуда».

Система встреч с удивительными предметами, разгадывание способов

их создания все это позволяет обеспечить интерес и продуктивность в поисковой деятельности школьников.

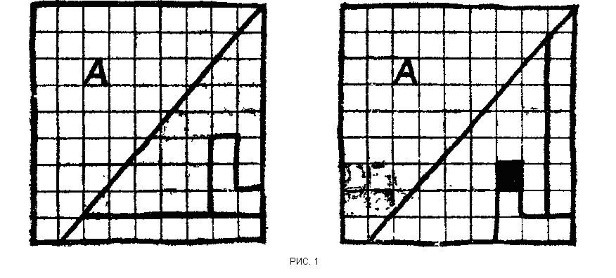
В качестве «Чуда» можно предложить задачу разрезания и складывание квадрата, и нахождения его площади (Рис. 1) [4].

Блоки 2. Содержательная часть урока.

Содержательная часть направлена в целом на развитие творческого воображения и фантазии учащихся и обеспечивает пропедевтику такой серьезной науки как теория решения изобретательских задач (автор – Г. С. Альтшуллер).

Здесь следует учитывать, что для отличных достижений при решении сложных задач важны три фактора: способности, возможности и индивидуальность. Способности к острому, живому восприятию, абстрактному и сложному мышлению, речевой, математической или технической легкости. Важно, чтобы эти способности были положительно оценены другими людьми.

Возможности должны включать ранние опыты, располагающие ребенка быть интеллектуально активным и заинтересованным в самостоятельном решении собственных проблем, в восприятии всего лучшего в окружающих, в восприятии себя как человека компетентного и уверенного. Именно на развитие данных качеств направлены содержание и методы организации обучения.

На столе у детей лежит обычный кусок проволоки, длиной 16 см.

Им предлагается решить такую задачу: какой формы должна быть клумба, чтобы мы могли обнести ее оградкой 16 м и она имела наибольшую площадь.

Чаще всего дети начинают прибегать к методу перебора, пытаясь с помощью проволоки составить форму клумбы. Данный метод не может нам дать точный ответ на нашу задачу. Площадь каких-то фигур нельзя вычислить точно, нельзя однозначно сказать площадь какой фигуры больше, в силу ограниченности знаний.

Значит нам нужен метод, который поможет дать однозначный ответ.

Итак, применим моделирование. А. Эйнштейн высоко ценил умение моделировать: «Осознание того, что наше сознание оперирует теоретическими моделями реальности, а не самой реальностью, является важнейшей особенностью современного научного подхода».

Моделирование – это, прежде всего, умение выделить главное. Модели должны быть по возможности простыми, однако они должны включать все самые важные части исследуемой системы (оригинала), самые важные функции и самые важные связи, внутрисистемные и внешние.

Обозначим основные шаги моделирования.

1. Понять задачу (оригинал).

Здесь нам на помощь приходит метод «мозгового штурма» основанный

а) на выдвижении альтернативных идей с их оценкой и развитием скрытых в них возможностей,

б) на преодолении психологической инерции.

Метод разработан и описан американским психологом Алексом Ф. Осборном в 1938 г., а окончательно сформировался и стал известен с выходом в 1953 г. книги Осборна «Управляемое воображение: принципы и процедуры творческого мышления».

2. Найти Главные части и построить модель задачи.

3. Найти основные связи между этими частями.

4. Провести исследование модели.

Прибегаем к инструментам ТРИЗ [3]. ТРИЗ основана на системном подходе, на глубоком изучении системы, которую надо улучшить. Чтобы улучшить

1. Определить Главную функцию системы, ответив на вопрос: «Зачем сделана система»?

2. Понять работу системы и определить части (подсистемы), участвующие в выполнении Главной функции.

3. Определить связи между этими частями.

А как определить, что это действительно главная часть или важная связь в системе? Если речь идет о решении задач, то главными могут быть части, связанные с нежелательным явлением, имеющем место в системе.

Есть простой способ. 1. Попробуйте части, участвующие в выполнении главной функции, исключить из системы. Если система или задача «рассыплется», то это – главная часть. 2. Попробуйте исключить связи между главными частями. Если система или задача «рассыпаются», то это – важная связь

Работая с формами и анализируя их, ребенок лучше усваивает и понимает связи, существующие в системе.

5. Перенести результаты исследования модели на оригинал.

После анализа известных школьникам форм они приходят к выводу, что клумба должна иметь форму квадрата.

Блок 3. Психологическая разгрузка.

Психологические и физиологические исследования показывают тесную связь между напряженной умственной и эмоциональной нагрузкой и напряжением скелетной мускулатуры, вегетативными сдвигами.

Общеизвестно, что систематические физические упражнения имеют огромное значение для поддержания работоспособности и здоровья.

Поддержание оптимального функционального состояния мозга осуществляется, кроме того, и путем регулирования выходящего из мозга эффекторного потока нервных импульсов. При помощи механизма саморегуляции обеспечивается дополнительное переключение центрального возбуждения на периферию, прежде всего скелетную мускулатуру и тем самым ослабление нервного напряжения.

Снижение психической напряженности на фоне мышечного расслабления проявляется в виде «раскрепощения» в общении, поведении, деятельности и проявлении чувств. В качестве психологической разгрузки можно использовать физические упражнения на гармонизацию развития полушарий головного мозга (следует помнить, что способность работать правой и левой рукой наравне удивительно благотворно для развития памяти, мышления и речи) а музыкальное сопровождение поможет создать благоприятную эмоциональную атмосферу.

Блок 4. Головоломки.

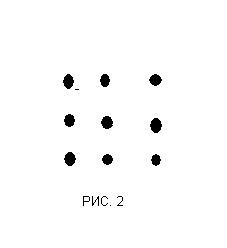
Головоломки представляют для школьника проблему, решение которой требует от него нетрадиционного поворота мысли. Главная функция его – развитие парадоксального, творческого мышления, смекалки, преодоление стереотипов мышления, развитие творческого воображения, в том числе, пространственного воображения. Кроме того, эта система головоломок пробуждает наблюдательность и любознательность, интерес ребенка к исследовательской деятельности и, как следствие, интеллектуальную активность. Например: соедините 9 точек четырьмя прямыми линиями, не отрывая руки и не обводя линий (рис. 2).

Интеллектуальная разминка, как и головоломки, позволяет обеспечить мотивацию учащихся и включить их в творческую деятельность на уроке.

Здесь можно дать задания:

• на создание схемы на основе существующего образа (такие задания развивают абстрактное мышление, а также выделение основных качеств и свойств объекта) – где еще можно применить полученное нами утверждение?
• на преодоление навязываемого заданием устойчивого образа, т. е. развитие способности выходить за пределы задачи, преодолевая инерцию мышления – выход из плоскости в пространство;
• на составление обратной задачи и применения решения в жизни.

Психологическая ценность данного компонента урока для учащихся заключается в том, что закрепляются способы и правила умственной работы; выявляются приемы, обеспечивающие повышенную продуктивность мышления; формируются навыки управления отдельными этапами творческого процесса принятия решений.

Блок 6. Резюме.

Последним блоком в структуре креативного урока является резюме. На этом этапе учитель подводит краткие итоги урока и устно осуществляет обратную связь с учащимися, выявляет их мнение об уроке. Как вариант, он просит детей оценить сам урок (интересно – не интересно, понравилось – не понравилось и т. д.), например, с помощью проволок сделать две рожицы – грустная и улыбающаяся. Показывая одну из них, дети дают оценку уроку. То есть речь идет о качественной и эмоциональной оценке урока. Возможны другие варианты оценки со стороны детей.

Развитие способностей к самоуправлению в творческой деятельности осуществляется через рефлексию. Рефлексия в школьном возрасте проявляется с двух сторон: как оценка задачи, которую надо решать, и как оценка своих ресурсов: могу ли я данную задачу решить.

Как показывает практика, применение ТРИЗ положительно влияет на развитие творческого мышления школьников [5]. А это говорит о том, что применение инструментов и реализация ТРИЗ необходима в современной системе образования.

Abstract: the article describes the TRIZ tools and methods for development of creative thinking. The author discusses the methods of simulation, decision theory, brainstorming, creative tasks, provides a description of a block of lessons.

Key words: brainstorming, modeling, creative thinking, systematic analysis.