Программа развития креативности у младших школьников на уроках математики, может быть реализована через три взаимосвязанных блока: диагностический, теоретический и практический. Рассмотрим пример такой программы.
1 Блок – диагностический.
Цель: изучение особенности развития креативного мышления у младших школьников.
Методы диагностики:
- анализ программы по математике, учебника по математике с целью выявить наличие упражнений и заданий по развитию креативности у школьников,
- наблюдение за учениками,
- анализ выполнения каждым учеником заданий на уроке,
- методика диагностика невербальной креативности (методика Е. Торренса, адаптирована А.Н. Ворониным, 1994)
Диагностика креативности Тест: Е. Торренса – Е. Е. Туник
Были проведены тесты:
– по определению технических способностей – тест Беннета,
– по определению уровня развития лингвистического мышления – субтест Айзенка,
– по определению уровня развития математических способностей – субтест Айзенка [1].
2 Блок – Теоретический
Развития творческого мышления младших школьников на уроках математики
Чем выше уровень творческого развития ученика, тем выше уровень его общего умственного развития, тем выше его работоспособность. Именно поэтому одна из задач, которые ставит перед собой современный педагог, – это развитие творческих способностей ученика.
Целенаправленное развитие теоретического мышления детей следует сочетать с совершенствованием творческого мышления.
Творческое мышление – высший уровень развития личности. Дж. Гилфорд считал, что уровень развития креативности (творческого мышления) определяется доминированием в мышлении четырех особенностей;
Оригинальность высказанных идей, стремление к интеллектуальной новизне.
Семантическая гибкость, т.е. способность видеть объект под разными углами зрения, способность обнаружить возможность нового использования данного объекта;
В-третьих, творческому мышлению свойственна образная адаптивная гибкость [2].
Способностью продуцировать разнообразные идеи в неопределенной ситуации.
Следует отметить, что творческие способности есть у каждого ребенка, но для каждого они индивидуальны и зависят не только от умственных способностей ученика, но и от определенных черт его характера, от созданных условий, которые содействовали бы развитию качеств и склонностей, обычно выделяемых как характерные черты личности.
Условия эффективного развития творческого мышления младших школьников.
Создаются ситуации выбора, процесс обучения включает задания, которые выполняются с учётом воображения;
Организуется сотворчество в детском коллективе с целого проявления и развития творческих способностей каждого;
Используются технологии развития творческого мышления;
Производится систематическое отслеживание результатов диагностики.
Творческое мышление лучше всего формировать в ходе решения задач нестандартного типа, когда ученик наталкивается на посильные для него проблемы и вопросы, формулирует их. Роль учителя – поставить учащегося в положение первооткрывателя, исследователя. Успешность решения таких задач зависит от уровня сотрудничества ученика и учителя, от овладения учеником системой умственных действий (сравнение, анализ, синтез и т. д.).
Специально отбираемые задания должны быть ориентированы на [1]:
– постепенное усложнение материала
– поэтапное увеличение объёма работы
– повышение уровня самостоятельности учащегося
– интеграцию заданий и способов деятельности
– привлечение элементов теории для решения задач
– обучение способам рассуждения с учётом принципа вариативности задач
– формирование беглости мыслей, оригинальность, гибкость ума, любознательность, умение выдвигать и разрабатывать гипотезы.
Важно развивать творчество младшего школьника, и здесь можно выделить следующие способы стимулирования творческих способностей.
- обеспечение благоприятной атмосферы;
- доброжелательность со стороны учителя, его отказ от критики в адрес ребёнка;
- поощрение высказывания оригинальных идей;
- использование личного примера творческого подхода к решению проблем;
- предоставление детям возможности активно задавать вопросы.
Роль уроков математики в развитии творческого мышления.
Свойство детского ума воспринимать все конкретно, буквально, неумение подняться над ситуацией и понять ее общий, абстрактный или переносный смысл – одна из основных трудностей детского мышления, ярко проявляющаяся при изучении такой абстрактной школьной дисциплины, как математика.
Современное содержание математического образования направлено главным образом на интеллектуальное развитие младших школьников, формирование культуры и самостоятельности мышления [3].
Анализ школьных программ по математике дает возможность расставить основные вехи развития творческого мышления школьников, поскольку овладение таким максимально абстрактным предметом, как математика, хорошо показывает, до какого максимума поднимается мышление школьников различных возрастов.
Каждая текстовая задача и добрая половина других упражнений, представленных в учебниках математики и дидактических материалах, и есть своего рода проблемы, над решением которых ученик должен задуматься, если не превращать их выполнения в чисто тренировочную работу, связанную с решением по готовому, данному учителем образцу. Только в этом случае обучение математике будет оказывать действенную помощь в решении образовательных, воспитательных и развивающих задач обучения, способствуя развитию познавательных способностей учащихся, таких черт личности, как настойчивость в достижении поставленной цели, инициативность, умение преодолевать трудности [4].
В соответствии с особенностями и целями применения разного рода задач, можно предложить следующую модель урока, направленного на развитие творческих способностей, как в системе специальных уроков развития, так и занятий по различным учебным предметам. Его структура может включать в себя 4 последовательных этапа:
Разминка.
Развитие психических механизмов, лежащих в основе творческих способностей учащихся (памяти, внимания, мышления, воображения)
Выполнение развивающих частично-поисковых задач.
Решение творческих задач, которые можно разделить на два типа: творческие задания, задачи повышенной трудности интегративного характера.
Для осуществления развивающих целей обучения необходимо активизировать познавательную деятельность, создать ситуацию заинтересованности.
Используя проблемы развития математических способностей учащихся, психолог В.А. Крутецкий приводит типы задач для развития активного самостоятельного, творческого мышления. Вот некоторые из них: задачи с несформулированным вопросом;
Задачи с недостающими данными;
В задачах этого типа отсутствуют некоторые данные, вследствие чего дать точный ответ на вопрос задачи не представляется возможным. Школьник должен проанализировать задачу и доказать, почему нельзя дать точного ответа на вопрос задачи, чего не хватает, что надо добавить. В скобках указываются пропущенные данные.
Например: Банка с медом весит 500 г. Такая же банка с керосином – 350 г. Сколько весит пустая банка? (Нужно знать отношение веса меда и керосина)
Задачи с излишними данными;
В эти задачи нарочито введены дополнительные ненужные данные, до известной степени маскирующие необходимые для решения показатели. Ученики должны выделить те данные, которые необходимы для решения, и указать на лишние, ненужные.
Например: Четыре гири разного веса весят вместе 40 кг. Определить вес самой тяжелой гири, если известно, что каждая их них втрое тяжелее другой, более легкой, и что самая легкая весит в 12 раз меньше, чем весят вместе две средних.
Задачи с несколькими решениями;
Для упражнения гибкости мышления важно, чтобы школьник умел находить несколько решений одной и той же задачи. Если эти решения неравноценны с точки зрения экономичности и рациональности, то ученик должен дать с этой точки зрения оценку каждому решению. Надо побуждать школьника найти наиболее рациональное, ясное, простое, изящное решение.
Например: Сколькими способами можно уплатить 78 руб., имея денежные знаки трех- и пятирублевого достоинства?
Задачи с меняющимся содержанием;
Необходимо перестроить содержание действия по решению задачи в соответствии с изменившимися условиями [5].
Такие задания заставляют размышлять, пробовать, ошибаться и, наконец, находить правильный ответ. Дети постоянно ищут рациональный способ решения, делают для себя открытия.
Задачи на соображение, логическое мышление.
На задачах этой серии тренируется способность логически рассуждать, смекалка и сообразительность. Не все эти задачи являются математическими в узком смысле слова, некоторые из них являются логическими задачами.
Например: В коробке лежат 16 шариков – черных, белых и красных. Красных шариков в 7 раз меньше, чем белых. Сколько в коробке черных шариков? (Решить и доказать. Доказать, что это – единственный вариант решения.)
Задания на развитие логики очень привлекают детей. А процесс решения, поиска правильного ответа, основанный на интересе к задаче, невозможен без активной работы мысли. В ходе таких игр и упражнений учащиеся постепенно овладевают умением самостоятельно вести поиск решения. Такие задачи развивают умственную активность, инициативу, творческое отношение к учебной задаче, помогают сохранить искру живого интереса к учёбе, к математике.
Таким образом, формирование творческого мышления на уроках математики, через решение определенного типа задач, в форме увлекательных игр, обогащают педагогический процесс, делает его более содержательным. Вызывает у детей богатое своими последствиями чувство удивления, живой интерес к процессу познания, помогает им усвоить любой учебный материал и влияет на ребенка, как на творческую личность. Такую работу необходимо проводить периодически, в течение всего учебного года.
3 блок – Формирующий.
3.1 Задание на смекалку.
Самый высокий уровень. Найди простой способ вычисления суммы всех чисел в ряду от 1 до 20.
Высокий уровень. Найди сумму такой пары чисел, чтобы можно было простым способом произвести вычисление. 1+2+3+…+18+19+20=
Средний уровень. Найди простой способ вычисления, соединив линиями пары чисел, как на рисунке.
Низкий уровень. Найди сумму каждой пары чисел, соединенных линиями. Вычисли простым способом сумму всех чисел. 1+2+3+…+18+19+20=
Итак, постановка вопроса о реализации и анализе использования проблемных ситуаций не является новой в методике преподавания математики, а требует лишь правильного использования всех тех ресурсов, которые скрыты в начальном курсе математики [3]. В этом блоке также могут быть использованы задачи отрытого типа [6].
3.2 Использование проблемных ситуаций на уроках математики [7].
В педагогической психологии разработано несколько вариантов определения уровня развития мышления у школьников. Так, А.3. 3ак исследовал общее различение школьников, по способу решения предложенных 22 задач: теоретическому или эмпирическому. Обобщенный способ (мышление теоретического типа) отличается тогда, когда задача решается не только для данного частного случая, но и для всех однородных. Необобщенный способ решения задач (решение только для данного частного случая) характеризует мышление эмпирического типа.
Эмпиричность подхода к решению задач выражается в ориентации лишь на непосредственно наблюдаемые или представляемые признаки, причем сначала собираются сведения о каждом объекте задачи отдельно, а затем результаты сопоставляются. Теоретический подход, наоборот, предполагает отвлечение от наглядных особенностей цели и условий задачи. Решение направлено на нахождение отношений, существенных для всех случаев, одинаковых с описанными в данной задаче.
Гилфорд предложил рассматривать три основные характеристики творческой личности – оригинальность (способность предлагать свой, необычный способ мышления), чувствительность и интеграцию. Последняя интерпретируется, как способность одновременно учитывать и/или объединять несколько противоположных условий, предпосылок или принципов. Торренс провел изучение креативного мышления и получил следующие результаты: креативность имеет пик в возрасте от 3,5 до 4,5 лет, а также возрастает в первые три года обучения в школе, уменьшается в последующие несколько лет и затем получает толчок к развитию.
3.3 Репродуктивные задания и упражнения, ориентированные на развитие психических механизмов, являющихся основой РТС [8].
В шестнадцати клетках каждой таблицы записаны вразнобой числа от 1 до 20.
Это означает, что какие-то четыре числа в каждой таблице пропущены. Без помощи ручки или карандаша, только глазами отследите все числа и выпишите недостающие.
Таблица 1 Таблица 2
|
2 |
19 |
9 |
8 |
|
20 |
11 |
8 |
17 |
|
20 |
1 |
14 |
16 |
3 |
13 |
6 |
2 |
|
|
18 |
12 |
7 |
5 |
16 |
4 |
14 |
18 |
|
|
10 |
4 |
15 |
13 |
7 |
15 |
10 |
5 |
В таблице 1 отсутствуют числа 3, 6, 11, 17; в таблице 2 – 1, 9, 12, 19.
3.4 Задания со сменой установки, преследуя конкретные дидактические цели, мы как бы обманываем ученика, пытаясь менять привычные приемы и условия выполнения репродуктивного задания [9].
Сравним, к примеру, следующие два подхода.
Первый вариант. При проверке усвоения таблицы умножения можно попросить ребят воспроизвести таблицу умножения на 4. Естественно, что при таком подходе трудно рассчитывать на возбуждение у детей интереса к работе и особой активности. Но если это же задание представить детям в ином, более интересном виде, то и результат будет совсем другим.
Второй вариант. Говорится: «Ребята, сегодня я дам вам задание, которое могли бы предложить будущим разведчикам для проверки у них быстроты реакции. Перед вами ряд чисел: 4, 15, 36, 8, 12, 5, 21, 24, 16, 3, 7, 20.
Как можно быстрее подчеркните те из них, которые делятся без остатка на 4».
Как показал опыт, такие задания дают возможность не только быстро и качественно проверить уровень знаний учащихся, но и стимулируют их познавательную активность.
Следующий вид репродуктивных заданий – задания с отсроченным вопросом. Их сущность заключается в том, что условие задания как бы изначально ориентирует ученика на уже привычный для него ход решения, который в итоге оказывается ошибочным. Подобная ситуация создается в том случае, когда вопрос, на который должен ответить ученик, оказывается для него неожиданны.
Например.
- Ребята, сейчас мы проверим вашу слуховую память и узнаем, какой у вас характер. Я громко и медленно назову шесть чисел. Ваша задача выслушать меня внимательно и записать эти числа в том же порядке. Начали: 5, 12, 10, 3, 8, 2.
- А теперь послушайте следующий ряд (называется, но уже не шесть, а больше чисел, в нашем случае – 12): 3, 21, 15, 48, 6, 10, 11, 16, 4, 5, 19, 9.
После паузы:
- Назовите лишь два числа данного ряда – самое большое и самое маленькое.
3.5 Следующий вид репродуктивных заданий – интегративные [2]. Они рассчитаны на интеграцию различных репродуктивных уровней знания и ценны тем, что позволяют в короткий срок выявить интересы учащихся.
Интегративность вопросов (чередование их из различных учебных дисциплин) и объединение в одном задании разных областей знаний являются логическим выражением реализации межпредметных связей в обучении. Именно они наиболее эффективно решают задачу уточнения и обогащения конкретных представлений учащихся об окружающей действительности (человеке, природе и обществе), и на их основе происходит формирование понятий, общих для разных учебных предметов.
Следовательно, интегрируя, мы работаем над сквозными понятиями, которые являются объектом изучения разных наук. Усваивая их на одном уроке, ученик углубляет свои знания об их признаках, обобщает их, устанавливает причинно-следственные связи.
Пример репродуктивной задачи интегративного характера.
Ира вспомнила, что в следующую пятницу – Международный женский день, а она еще не приготовила маме подарок. Какое это было число? (1марта).
В целях развития логического мышления учащихся нужно предлагать им самостоятельно производить анализ, синтез, сравнение, классификацию, обобщение, строить индуктивные и дедуктивные умозаключения. Такая возможность предоставляется в условиях выполнения логически-поисковых заданий, которые обеспечат преемственность перехода от простых формально-логических действий к сложным, от заданий на репродукцию и запоминание – к истинно творческим.
Частично-поисковая задача содержит такой вид задания, в процессе выполнения которого учащиеся, как правило, самостоятельно или при незначительной помощи учителя открывают новые для себя знания и способы их добывания,
К конкретным частично-поисковым задачам можно отнести, например, такие задания: на нахождение закономерности; на нахождение принципа группировки и расположения приведенных слов, цифр, явлений; на подбор возможно большего количества примеров к какому-либо теоретическому положению; на нахождение нескольких вариантов ответа на один и тот же вопрос; на нахождение наиболее рационального способа решения; на усовершенствование какого-либо задания и т. д.
Проанализируйте следующие ряды чисел, выявите закономерность и продолжите их запись:
1, 3, 4, 7, 11, 18…
2, 8, 3, 7, 4, 6...
Помимо ответа на вопрос поисковой задачи, рекомендуется давать задания на выяснение способа ее решения, то есть системы логических операций, применяемых при решении.
Особое место следует отводить подбору таких заданий, которые имеют внешнее сходство при разных содержании и способах решения.
3.6 Ребус – это своеобразная загадка, которая изображается при помощи букв, фигур, знаков. В примерах все слова ребусов изображены при помощи букв. Как их разгадывать? Если буквы нарисованы одна в другой, то их названия читаются с прибавлением буквы «в»; если одна буква находится под другой, то читать их надо с прибавлением «на», «над» или «под»; если между буквами стоит знак плюс (+), это означает прибавление буквы «с» или «и». Еще одна буква может быть расположена «у» или «за» какой-то [4].
- Разгадайте внешне похожие ребусы: 1ОЧКА, 1БОР, Ш1А, Ф1А, 2Д, ПО2Л (Одиночка, разбор, школа, фраза, парад, подвал.)
Для развития творческих способностей младших подростков огромное значение имеют такие частично-поисковые задания, которые содержат несколько вариантов решения. Выполняя их, учащиеся должны самостоятельно выявлять эти варианты (как можно большее их количество) и по возможности определять наиболее рациональные из них.
Например:
Посмотрите на это выражение: 9 + 8 = 5. С точки зрения математики это полный абсурд. Но все же подумайте и попытайтесь сообразить, догадаться, в какой ситуации оно будет верно.
Разумеется, учащиеся будут вначале озадачены: ведь 9 + 8 = 17. В процессе поиска ответа они дадут Различные варианты трактовки этого выражения, пока не придут к мысли, что в какой-то ситуации 5 может быть равно 17. В итоге, как правило, приходит догадка, что это возможно на «языке часов». Так, если к девяти часам утра прибавить восемь, получится семнадцать часов дня, а в разговорной речи – пять часов. Красивый ответ! Не правда ли?
Из геометрии:
|
80 |
о |
|
90 |
п |
|
100 |
? |
Ответ: «т» (80 – острый угол, 90 – прямой, 100 – тупой).
Работая много лет в условиях Крайнего Севера из-за многочисленных актированных дней, главная задача учителя – отработать программный материал. Но я нашла выход для выполнения этой работы: этот материал можно использовать не только на уроках математики, но и на других уроках.
3.7 Головоломки [3]
Головоломки не только занимательны, но и полезны; кроме того, они отлично развивают мышление. Самые лучшие головоломки – это задачи, не требующие специальных знаний, то есть такие, которые любой человек может решить при помощи не специальных формул, а собственного интеллектуального потенциала. Возьмем такую задачу:
Вы написали четыре письма и надписали четыре конверта для них. Письма в конверты вы вкладываете наугад. Каков процент вероятности, что только три письма оказались в своих конвертах?
На первый взгляд задача кажется очень трудной, но это только в том случае, если мы будем искать для ее решения специальные формулы. Но здесь они не нужны, и каждый может путем простейших логических размышлений найти правильный ответ.
Ответ: вероятность того, что только три письма окажутся в нужных конвертах, равна нулю, Если три письма из четырех оказались в своих конвертах, остается только одно письмо и один конверт для него, и в этот конверт, следовательно, также попадет нужное письмо.
Головоломки
1. В данном ряду слов переместите одно слово так, чтобы последовательность была в алфавитном порядке.
ПРОСО, ФЛЯГА, ВИЗАВИ, АВРАЛ, ТАБУ.
2. В 6 утра путешественница отправилась к отелю на вершине горы. Она добралась до отеля в шесть часов вечера того же дня. В отеле она переночевала и ровно в шесть утра отправилась в обратный путь по тому же самому маршруту. Она оказалась у подножия, в той точке, откуда начала путь, ровно в шесть часов вечера того же дня.
Была ли на ее пути такая точка, в которой она побывала в одно и то же время по дороге наверх и по дороге вниз?
Можно ли с уверенностью утверждать, что такая точка существует? Объясните свой ответ…
3. Замените вопросительный знак в последней ячейке фигурой.
Развивайте интеллект


4. Найдите лишнее число. 79316
64256 45180 29116 51204 82246 32128
5. Человек гуляет с собакой, ведя ее на поводке; они движутся со скоростью 3 км/час. Постепенно они приближаются к дому, и когда до дома остается 7 километров, хозяин отпускает собаку. Пес тотчас же устремляется к дому и бежит со скоростью 8 км/час. Когда пес добегает до дома, он поворачивает обратно и бежит к хозяину с той же скоростью. Добежав до хозяина, он вновь бежит к дому. Так повторяется до тех пор, пока человек сам не доходит до дома и не впускает собаку в дом. Сколько километров пробежала собака с того момента, как хозяин спустил ее с поводка, до того момента, как он подошел к дому? Подсказка дана на странице 106.
6. Какая фигура здесь лишняя? [5]
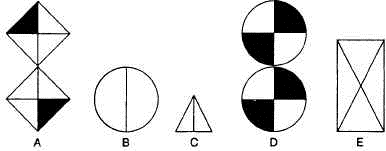 Блок «головоломки» также являться ключевым в система непрерывного образования НФТМ-ТРИЗ М. М. Зиновкиной [11].
Блок «головоломки» также являться ключевым в система непрерывного образования НФТМ-ТРИЗ М. М. Зиновкиной [11].Таким образом,одной из важных задач учителя является формирование творческого мышления у младшего школьника. Реализация данной задачи возможна при специально созданных условиях, при определенных способах его стимулирования и использовании на уроках технологий развития творческого мышления, в т.ч. проблемного обучения. Так как именно оно вносит большой вклад в формирование готовности к творческой деятельности, способствует развитию познавательной активности, обеспечивает более прочное и осознанное усвоение знаний; развивает аналитическое мышление, делает учебную деятельность для учащихся более привлекательной, основанной на постоянных трудностях.
Таким образом, единственным плодотворным путем развития творческого мышления в детстве становится максимально полное раскрытие потенциальных возможностей, природных задатков, и учитель должен создать такую полноценно развивающуюся деятельность для учащихся, чтобы потенциал не остался не востребованным.
Ссылки на источники
- Зак А.З. Развитие интеллектуальных способностей у детей 8 лет: Учебно-методическое пособие для учителей. – М.: Новая школа, 2012. – 252с.
- Выготский Л.С. Воображение и творчество в детском возрасте: Психологический очерк: Книга для учителя. 3 изд. – М.: Просвещение, 2011. – 93 с.
- Дереклеева Н.И. Мастер-класс по развитию творческих способностей учащихся. Учебное издание. Методическая библиотека. – М. Знание, 2008.-с. 14-17.
- Федеральный государственный образовательный стандарт общего образования. – М. 2011. – с.4
- Зак А.З. Развитие интеллектуальных способностей у детей 9 лет: Учебно-методическое пособие для учителей. – М.: Новая школа, 2011. – 108 с.
- Утёмов В. В. Задачи открытого типа как средство развития креативности учащихся средней школы // Концепт: научно-методический электронный журнал официального сайта эвристических олимпиад «Совёнок» и «Прорыв». – 4 квартал 2011, ART 11-4-02. – Киров, 2011 г. – URL: http://www.covenok.ru/koncept/2011/11402.htm. – Гос. рег. Эл № ФС 77-46214. – ISSN 2225-1618.
- Селевко Г. К. Современные образовательные технологии // Школьные технологии. – 2009. – №6.
- Брушлинский А.В. Психология мышления и проблемное обучение. – М.: Знание, 2009. – 96 с.
- Сереброва И.В. Развитие внимания и логического мышления на уроках по математике // Начальная школа. – 2009. – №6. – с.51-53.
- Крутецкий В.А. Проблема способностей в психологии: (В помощь лектору). – М.: Знание, 2011. – 62 с.
- Зиновкина М. М. Многоуровневое непрерывное креативное образование в школе // Концепт. – 2012. – № 9 (сентябрь). – ART 12116. – 1,0 п. л. – URL: http://www.covenok.ru/koncept/2012/12116.htm. – Гос. рег. Эл № ФС 77- 49965. – ISSN 2304-120X.
Bitsuk Natalia,
mathematics teacher of Municipal state educational institution of Gydansky boarding school of the secondary (full) general education, Yamalo-Nenets Autonomous Area, page of Gyd, Tazovsky district.
bicuk_55.78@mail.ru
Development of creativity in younger school students at mathematics lessons
Summary. In article the program of development of creativity at younger school students at mathematics lessons is considered. The author describes a detailed plan of the program which includes three blocks: diagnostic, theoretical and practical. The first block is directed on studying of a level of development of creativity at the younger school students, the second block is directed on studying of a theoretical material on a problem of research of development of creativity at younger school age, and the third block promotes development of creativity in younger school students.
Keywords: creativity, school students, creativity, tasks.
