В период научно-технической революции и быстрого нарастания потока научной информации основной задачей современной школы становится формирование активной, творческой, компетентностной личности, способной успешно ориентироваться и обустраиваться в современном обществе.
На современном этапе развития науки, техники и производства, обществу нужны новаторы, рационализаторы, изобретатели – люди, умеющие мыслить творчески, способные создавать новое во всех областях жизни [1]. Если внимательно рассмотреть поведение человека, его деятельность в любой области, то можно выделить два основных вида познавательной деятельности, находящихся в определенном отношении. Одни действия человека можно назвать воспроизводящими или репродуктивными. Такой вид деятельности тесно связан с нашей памятью и его сущность заключается в том, что человек воспроизводит или повторяет уже ранее созданные и выработанные приемы поведения и действия.
Кроме репродуктивной деятельности в поведении человека присутствует творческая деятельность, результатом которой является не воспроизведение бывших в его опыте впечатлений или действий, а создание новых образов или действий. В основе этого вида деятельности лежат творческие способности. Таким образом, если познавательная деятельность зависит от творческой, то с уверенностью можно сказать, что развитие познавательных способностей детей в решающей степени зависит от их творческой деятельности. При этом наиболее эффективной является систематическая творческая деятельность учащихся [2].
В обучении профессиональному творчеству в нашей стране особое место занимает теория решения изобретательских задач – ТРИЗ. Ее разработка и распространение связаны с именем инженера-изобретателя, писателя-фантаста Г. С. Альтшуллера.
ТРИЗ – это научно-практическое направление по разработке и применению эффективных методов решения творческих задач, генерированию новых идей и решений в науке, технике и других областях человеческой деятельности. Основным теоретическим положением ТРИЗ является утверждение, что технические системы развиваются по объективным, познаваемым законам, которые выявляются путем изучения больших массивов научно-технической информации (в том числе патентной) и истории техники. Эти законы можно использовать при улучшении существующих и разработке новых систем.
Среди основных особенностей ТРИЗ можно отметить следующие:
1. Использование закономерностей развития систем, на основе которых разработаны законы развития технических систем и методология их прогнозирования.
2. Выявление и разрешение противоречий, возникающих при развитии систем. Из всех известных эвристических методов только в ТРИЗ сформулированы методы поиска, обострения и разрешения противоречий на разных системных уровнях, разработаны приемы для разрешения противоречий, система типовых сильных решений.
3. Систематизация различных видов психологической инерции и использование методов ее преодоления.
4. Развитие многоэкранного (системного) стиля мышления и использование специальных системных операторов.
5. Методика поиска ресурсов – вещественных, энергетических, информационных и других, которые позволяют решить творческую задачу, внося в систему минимальные изменения и обеспечивая легкую внедряемость решения.
6. Структурирование информации о проблемной ситуации, использование специальных графических методов.
7. Специальное информационно-методическое обеспечение: методики анализа и решения задач, графические методы и диаграммы, таблицы и указатели применения эффектов и явлений и др.
В рамках ТРИЗ разработана методика прогнозирования чрезвычайных ситуаций, вредных и нежелательных явлений. Она предназначена для решения проблем, связанных с обеспечением безопасности, с выработкой конкретных творческих решений, направленных на предотвращение спрогнозированных нежелательных явлений.
ТРИЗ может эффективно применяться практически во всех областях человеческой деятельности:
- для решения творческих задач;
- прогнозирования развития существующих и разрабатываемых систем;
- обеспечения повышения качества творческого мышления.
На земле нет областей человеческой деятельности, где не требуется постоянного увеличения доли творчества. ТРИЗ развивает системный и диалектический образ мышления, применимый к любым жизненным ситуациям. ТРИЗ позволяет понимать происходящие события в широких областях деятельности – социальных, научных, технических и др. ТРИЗ развивается не только вглубь, но и вширь. ТРИЗ – это наука о творчестве. Творчество, всегда считавшееся неопределенным явлением человеческой жизни, вышло на уровень точной науки.
Долгое время единственным инструментом решения творческих задач – задач, не имеющих четких механизмов решения, – был «метод проб и ошибок».
В XX веке резко возросла потребность в решении творческих задач. Это привело к появлению различных модификаций «метода проб и ошибок». Наиболее известны из них «мозговой штурм», «синектика», «морфологический анализ», «метод контрольных вопросов».
Суть этих методов – повысить интенсивность генерации идей и перебора вариантов. Главная проблема при их использовании – можно сэкономить время на генерации идей, но это приводит к большим затратам времени на их анализ и выбор наилучшего варианта.
Г. С. Альтшуллер поставил задачу иначе: «Как без сплошного перебора вариантов выходить сразу на сильные решения проблемы?»
Решить эту задачу помогут принципы, лежащие в основе ТРИЗ.
- Принцип объективности законов развития систем – строение, функционирование и смена поколений систем подчиняются объективным законам. Cильные решения – это решения, соответствующие объективным законам, закономерностям, явлениям, эффектам.
- Принцип противоречия – под воздействием внешних и внутренних факторов возникают, обостряются и разрешаются противоречия. Проблема трудна потому, что существует система противоречий скрытых или явных. Системы эволюционируют, преодолевая противоречия на основе объективных законов, закономерностей, явлений и эффектов. Сильные решения – это решения, преодолевающие противоречия.
- Принцип конкретности – каждый класс систем, как и отдельные представители внутри этого класса, имеют конкретные особенности, облегчающие или затрудняющие изменение конкретной системы. Эти особенности определяются ресурсами: внутренними – теми, на которых строится система, и внешними – той средой и ситуацией, в которой находится система. Сильные решения – это решения, учитывающие конкретные особенности конкретных систем, а также индивидуальные особенности, связанные с личностью конкретного человека, решающего проблему [3.]
На сегодняшний день главной целью педагогической деятельности можно считать создание условий для развития творческих способностей личности учащихся. Творческая способность – это способность увидеть, проблему, мобилизовать необходимые знания для выдвижения гипотезы, способность теоретически и практически проверить её и в результате создать оригинальный продукт, научное открытие, изобретение, решение задачи [1].
 Рис.1
Рис.1Так как элемент творчества может присутствовать в любом виде человеческой деятельности, то справедливо говорить не только о художественных творческих способностях, но и о технических творческих способностях, о математических творческих способностях, и т. д.
Математика – это не только серьезная фундаментальная наука и основа научно-технического прогресса, но и весомая часть культуры человечества, инструмент познания мира, благодатная почва для развития творческих способностей. Математика является важной учебной дисциплиной для многих профилей обучения. Она имеет большие возможности для развития логического мышления, практических действий по моделированию геометрических и реальных объектов [4]. Учебные математические задачи являются очень эффективным и часто незаменимым средством усвоения учащимися понятий и методов школьного курса математики. Велика роль задач в развитии математического мышления и в математическом воспитании учащихся, в формировании у них умений и навыков в практическом применении математики. Решение задач служит достижению всех тех целей, которые ставятся перед обучением математике. А приемы решения текстовых задач выступают как средство обучения способом рассуждений, анализу ситуации, выбору стратегии решения задач. В обучении решению задач используются для записи условия схематические рисунки, модели, позволяющие представлять рассматриваемую ситуацию наглядно, без которых трудно понять логику рассуждений. Ведь предлагая школьнику нарисовать четырехугольник, учитель ставит его перед множеством проблем: что такое четырехугольник, какой из четырехугольников изобразить, как его расположить, какого размера он должен быть? Работа по освоению учащимися опыта эмоциональной и творческой деятельности, прежде всего, заключается в развитии мышления через разные его виды. Начинается эта работа с простых и доступных каждому ученику заданий.
Необходимо особо отметить, что не стоит готовить творческие задания персонально для наиболее способных учащихся и предлагать их вместо обычных заданий, которые даются всему классу. Такой способ индивидуализации нельзя считать лучшим, поскольку он ставит в заведомо неравные условия детей, делит их на способных и неспособных. Задания творческого характера должны даваться всему классу. При их выполнении оценивать следует только успех. Необходимо всегда внимательно выслушивать ученика, видеть в каждом школьнике индивида с особыми возможностями и дарованиями. Так, известный американский психолог Розенталь утверждал, что в ситуации, когда педагог ожидает выдающихся успехов от детей, они действительно этих успехов начинают добиваться, даже если раньше считались не очень способными [5].
У каждого ребенка есть способности и таланты, дети от природы любознательны и полны желания учиться. Для того чтобы они могли проявить свои дарования, нужно умное руководство со стороны взрослых. Как сказал Лев Николаевич Толстой: «Если ученик в школе не научился сам ничего творить, то и в жизни он всегда будет только подражать, копировать, так как мало таких, которые бы, научившись копировать, умели сделать самостоятельное приложение этих сведений».[6] Следовательно, задачи педагога – использовать разнообразные методы обучения, систематически, целенаправленно развивать у школьников подвижность и гибкость мышления, настойчиво стимулировать процессы перестройки, переключения, поисковой активности. Учитель должен учить детей рассуждать, гибко подходить к проблемам, не зубрить, а мыслить, самим делать выводы, находить новые, оригинальные подходы, получать изящные результаты, красивые решения, чтобы ощутить удовольствие от обучения [5].
Чтобы любой урок математики был направлен на развитие творческих способностей учащихся и реализовал их, учителю необходимо при его проведении ориентироваться на следующие принципы:
- Использовать современные педагогические развивающие технологии, ориентированные на развитие способности учащегося быть субъектом образовательной деятельности как процесса своего развития в целом: и телесного, и эмоционального, и интеллектуального, и личностного, и духовно-нравственного.
- Принцип «принятия другого». Согласно данному принципу учитель должен изначально принимать ученика как индивидуальность, имеющую право быть личностью со своими, уже сложившимися особенностями. Это означает, что отношение ученик – учитель уже не может строиться по логике объективно-субъектного взаимодействия.
- Принцип проектирования и реализации образовательной среды, способствующей раскрытию творческих способностей учащихся. Принцип «самосознающей позиции», т. е. умение встать в рефлексивную (самосознающую) позицию по отношению к тому, чему учить, как учить и зачем учить.
- Принцип сотрудничества. Чтобы на любом уроке у учащихся была возможность развивать свои творческие способности, учителю в ходе проведения урока (факультатива, занятия) необходимо обращать внимание на: способность учащихся быстро схватывать смысл принципов, понятий, логических построений; потребность и способность длительно сосредотачиваться на заинтересовавших ребенка сторонах проблемы и стремление разобраться в них; способность подмечать, рассуждать и выдвигать объяснения, в том числе необычные: повышенную молчаливость или же, напротив, повышенную потребность в постоянном высказывании и отстаивании своего мнения.
Обязательные условия проведения урока, направленного на развитие творческих способностей учащихся, можно сформулировать следующим образом:
- Учитель должен принимать все ответы и реакции детей (устные и письменные ответы; ответы, имеющие литературную и нелитературную форму; ответы в графической и пластической формае, в форме поведения и реакции на другого человека).
- Необходимо обеспечить независимость выбора и принятия решений учащимися для того, чтобы они могли самостоятельно контролировать собственное продвижение.
- Каждой идеей ученика учитель должен восхищаться.
- Ошибка ученика должна использоваться как возможность нового, неожиданного взгляда на что-то привычное.
- Непременным условием проведения урока является положительная поддержка личности каждого ребенка.
- Во время урока исключается всякая критика личности и деятельности детей.
- Следует шире использовать в учебной деятельности повседневный опыт детей [5].
Ученые отмечают, что развить сразу весь комплекс свойств, входящих в понятие «творческие способности», невозможно. Это длительная, целенаправленная работа, поэтому эпизодическое использование творческих задач не принесет желаемого результата. Познавательные задания должны составлять систему, позволяющую формировать и развивать все многообразие интеллектуальной и творческой деятельности учащихся и обеспечивать переход от репродуктивных формально-логических, действий к творческим. Необходимо также помнить, что творческие способности рассматриваются как то, что не сводится к знаниям, умениям, навыкам, но объясняет (обеспечивает) их быстрое приобретение, закрепление и эффективное использование на практике. Поэтому нельзя не отметить огромное значение для развития творческих способностей школьников уровня развития психических механизмов – памяти, внимания, воображения и др. Именно эти качества, по данным психологов, являются основой развития продуктивного мышления и творческих способностей учащихся.
Упражнения в решении составных заданий, в сравнении выражений, требующие использования известных детям закономерностей и связей в новых условиях, упражнения геометрического содержания, которые часто требуют переосмысления приобретенных ранее знаний, и другие должны быть использованы для постановки детьми проблемных задач. Только в этом случае обучение математике будет оказывать действенную помощь в решении образовательных, воспитательных и развивающих задач обучения, способствуя развитию познавательных способностей учащихся, таких черт личности, как настойчивость в достижении поставленной цели, инициативность, умение преодолевать трудности. Любое математическое задание ставит ученика перед определенными трудностями, требующими значительного умственного усилия при выполнении мыслительных операций, приводящих к решению. Проблемные задания ставят ученика в ситуацию, в которой у него должно появиться удивление и ощущение трудности, или одно только ощущение трудности, которое, однако, ученик намерен преодолеть.
Проблемное обучение – это организация учебных занятий, которая предполагает создание под руководством учителя проблемной ситуации и активной самостоятельной деятельности учащихся по их разрешению, в результате чего и происходит творческое овладение решением, профессиональными знаниями, умениями и навыками, развитие мыслительных способностей. Проблемность при обучении математике возникает совершенно естественно, не требуя никаких специальных упражнений, искусственно подбираемых ситуаций. В сущности, не только каждая текстовая задача, но и большая часть других упражнений, представленных в учебниках математики и дидактических материалах, и есть своего рода проблемы, над решением которых ученик должен задуматься, если не превращать их выполнения в чисто тренировочную работу, связанную с решением по готовому, данному учителем образцу.
На мой взгляд, классная и внеклассная работа должны иметь возможность не только развивать и поддерживать интерес к математике, но и способствовать развитию креативности, мыслительной деятельности личности – умению выделять главное в проблеме; формированию высокого уровня элементарных мыслительных операций (анализа и синтеза, сравнения, аналогии, классификации), высокого уровня активности мышления, переходящего в творческое, когда способен осознавать собственные способы мышления, действовать в нестандартной обстановке.
Важнейшими математическими операциями являются анализ и синтез.
Анализ связан с выделением элементов данного объекта, его признаков или свойств. Синтез–соединение различных элементов, сторон объекта в единое целое. В мыслительной деятельности анализ и синтез дополняют друг друга.
Формированию и развитию данных мыслительных операций способствует решение задач, в которых от учащихся требуется проводить правильные рассуждения, рассматривать объекты с разных сторон, указывать их различные и схожие свойства, а также ставить различные вопросы относительно данного объекта. Приведу примеры таких задач, которые я использую на уроках математики в 6-м классе:
1) Как разрезать фигуру на четыре равные части?


2) Лиза, Галя и Нина жили в разных домах. Дом № 1 – высокий каменный, № 2 – высокий деревянный, № 3 – невысокий каменный. В каком доме жила каждая из девочек, если Галя и Нина жили в высоких, а Нина и Лиза – в каменных?
3) Четырьмя двойками. Можно ли четырьмя двойками выразить число 111? Выполните задание четырьмя способами.
Становление креативной личностиможно определить как формирование и развитие личности, адекватной выполняемой творческой деятельности и получаемым творческим результатам. Темп и траектория этого процесса детерминируются биологическими и социальными факторами, собственной активностью личности и ее креативными качествами, а также обстоятельствами, жизненно важными событиями и профессионально обусловленными факторами. Возникает тесная взаимосвязь становления креативной личности и креативного образования. Отсюда следует зависимость уровней профессионально-творческой деятельности человека, достигаемых результатов и уровней его креативной подготовки как готовности к их выполнению и достижению [7].
Развитию креативности способствует и аналогия. Использование аналогии в математике является одним из основных методов при поиске доказательства теоремы, решении текстовых задач. Для формирования умения проводить аналогию можно использовать задачи на нахождение словесных аналогий, аналогий между различными объектами. Например, по аналогии с первой парой подберите недостающее слово в другой паре:
1) влево – вправо, вверх – …
2) сумма – сложение, частное – …
3) квадрат – куб, круг – …
4) уменьшаемое – вычитаемое, делимое …
Такие упражнения развивают воображение учащихся и играют немалую роль в формировании креативности мыслительной деятельности. Кроме того, систематические упражнения такого рода дают возможность усвоить алгоритм нахождения аналогов – по функциям, по признакам, по подсистемам.
Классификация – следующий прием мышления, способствующий развитию креативности. Суть его – в разбиении множества рассматриваемых явлений или объектов на попарно пересекающиеся подмножества. Подобные задачи способствуют развитию умения «узнавать» знакомые объекты, переносить знания в непривычную ситуацию, видеть структуру объекта. Например, найдите «лишнее» число: -1,5;-3;2;2,8;-0,6
Обобщение говорит о степени развития мыслительной деятельности, осознанности, прочности усвоения и объеме знаний учащихся. Например, дайте общее название объектам, входящим в одну группу:
А) 3 и -3; 7 и -7; 2,5 и -2,5 – это….
Б) парабола, гипербола, прямая – это…
В) параллелограмм, трапеция, прямоугольник – это…
Г) 1,4,9,16,25, 36,49,64,81,100 – это…
Решение задач-головоломок, ребусов, занимательных задач, задач на смекалку так же способствует развитию креативности. При выполнении таких задач учащимся чаще всего приходится пользоваться методом проб и ошибок, что, в конечном счете, развивает интуицию, творчество, способность искать другой способ решения, отказавшись от ложного пути. Поиск решения таких задач воспитывает усидчивость, развивает различные виды памяти, внимание.
Развитие креативности, умения самостоятельно конструировать свои знания лежит и в основе метода проектов. Первыми проектами для школьников становится домашнее задание, которое они готовят для своих одноклассников. Так, при прохождении темы «Координаты точки» в 6-м классе, на уроке я провожу практическую работу, выдаю ребятам карточки с координатами точек. Они изображают эти точки в координатной плоскости в определенной последовательности и получают какой-то рисунок (черепаха, сердечко, слон и т. д.). Домой ребятам даю задание придумать свой рисунок в координатной плоскости и выписать координаты каждой точки. Таким образом, каждый ученик имеет индивидуальное творческое задание, а я имею возможность проверить, как усвоена тема. В 8-м классе на уроках геометрии при обобщении главы «Четырехугольники», прошу учащихся придумать сказку или стихотворение об изученных геометрических фигурах.
Полезность проекта заключается в том, что мы не рассказываем ребенку ничего лишнего. У него есть право выбора первого шага, хода и даже цели проекта. Идя к этой цели, он сталкивается с тем, что ему приходится "добывать" знания, а затем соединять разрозненные сведения. Он черпает из разных предметных областей только необходимые знания и использует их в той деятельности, которая ему интересна [8].
Развитию познавательных интересов способствует использование геометрического материала. Это такие задания, как рисование картины с помощью только геометрических фигур, изготовление многогранников, скульптуры из многогранников и геометрических тел. При выполнении многогранников ребята настолько творчески подходят к процессу, что выбирают различные материалы для изготовления и раскрашивают грани в различные цвета. Из лучших работ в кабинете организована выставка.
Математика и история – две неразрывные области знания. Сведения из истории математики, исторические задачи сближают эти два школьных предмета. История обогащает математику гуманитарным и эстетическим содержанием, развивает образное мышление учеников. Математика, развивающая логическое и системное мышление, в свою очередь занимает достойное место в истории, помогая лучше ее понять.[8] В зависимости от типа урока и изучаемой темы я использую различные формы подачи исторического материала. Например, при изучении теоремы Пифагора в 8 классе заранее прошу учащихся подготовить сообщения и презентации о биографии Пифагора и истории доказательства самой теоремы, а на уроке решаем старинные задачи, в которых применяется изученный материал.
1) Задача индийского математика XII века Бхаскары
«На берегу реки рос тополь одинокий
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?» [9].
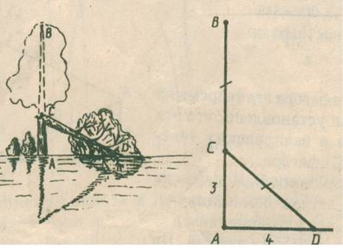 Рис.2
Рис.22) Случится некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обреете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать [10].


Рис.3
Развитие творческого мышления неотделимо от формирования исполнительских умений и навыков. Чем разностороннее и совершеннее умения и навыки учащихся, тем богаче их фантазия, реальнее их замыслы, тем более сложные математические задания выполняют школьники.
Развитие творческого мышления неотделимо от формирования исполнительских умений и навыков. Чем разностороннее и совершеннее умения и навыки учащихся, тем богаче их фантазия, реальнее их замыслы, тем более сложные математические задания выполняют школьники.
Психологами установлено, что развитие мышления человека неотделимо от развития его языка. Поэтому важнейшая задача в развитии творческого мышления учащихся – обучение их умению словесно описывать способы решения задач, рассказывать о приемах работы, называть основные элементы задачи, изображать и читать графические изображения ее. Усвоение учащимися необходимого словарного запаса очень важно для формирования и развития у них внутреннего плана действия. На уроках я стараюсь добиваться того, чтобы ученики, не стесняясь, высказывали свое мнение, четко и грамотно комментировали решение задач [11].
Большое внимание на своих уроках я уделяю так же самостоятельной работе учащихся. Самостоятельная учебная деятельность имеет не только учебное, но и личное, и общественное значение. Это организуемая самим школьником в силу своих внутренних познавательных мотивов в наиболее удобное время, контролируемая им самим в процессе, и по результату деятельности на уроке, и в ходе домашней самоподготовки.
Таким образом, нестандартные приемы, активные методы, творческие задания – все это в целом благотворно влияет на воспитание ученика, на мотивацию к обучению. И результатов учитель добивается тогда, когда введение в область математических знаний совершается в легкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранные с надлежащим остроумием и занимательностью.
Ссылки на источники
- Горинов А.В. Развитие творческих способностей школьников на уроках физики http://gigabaza.ru/doc/52436.html
- Кравченко А.Н. Развитие творческих способностей учащихся через нестандартные формы работы на уроках математики http://ansinyakova.ucoz.ru/publ/razvitie_tvorcheskikh_sposobnostej_uchashhikhsja_cherez_nestandartnye_formy_raboty_na_urokakh_matematiki/1-1-0-2
- Утёмов В. В., Зиновкина М. М. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ // Концепт. - 2013. - Современные научные исследования. Выпуск 1. - ART 53572. - URL: http://e-koncept.ru/2013/53572.htm. - Гос. рег. Эл No ФС 77-49965. - ISSN 2304-120X. [Дата обращения: 17.12.2014]
- Леонкин М.И.Развитие творческих способностей учащихся на уроках математики http://anone.ru/news/razvitie_tvorcheskikh_sposobnostej_uchashhikhsja_na_urokakh_matematiki/2014-01-07-420
- Матус З.Г. Развитие творческих способностей на уроках математики http://festival.1september.ru/articles/512280/
- Толстой Л.Н. Полное собрание сочинений т.8,с.118
- Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: Прикладной курс научного творчества: Учебное пособие. – Киров: АНОО «Межрегиональный ЦИТО», 2013. – 212 с
- Хатина О.Г. Развитие творческих способностей на уроках математики http://ext.spb.ru/index.php/2011-03-29-09-03-14/95-maths/2959-2013-05-17-18-29-01.html
- Шнайдер И.И. Урок-путешествие по теме: «Применение теоремы Пифагора при решении задач». http://nsportal.ru/shkola/geometriya/library/2013/01/20/urok-puteshestvie-po-teme-primenenie-teoremy-pifagora-pri
- Иванова Н.Н. Теорема Пифагора. http://festival.1september.ru/articles/599696/
- Ершова Г.П. Развитие творческих способностей на уроках математики http://www.pandia.ru/text/77/150/7602.php
Bogatyreva Natalya
the advanced qualification category teacher
of Math Educational Institution “Secondary Educational School №31” Podolsk
The development of pupils’ intellectual qualities and creative abilities at Math lessons
Annotation. This article demonstrates the reveals characterize the creative mind, examples of logical tasks and exercises. They help in development of pupils’ creative potential and more over shows principles and conditions of realization of Math lesson aimed at the development of pupils’ intellectual qualities and creative abilities.
