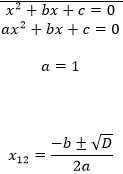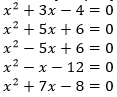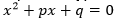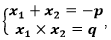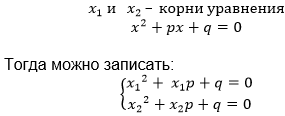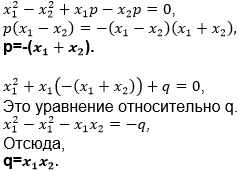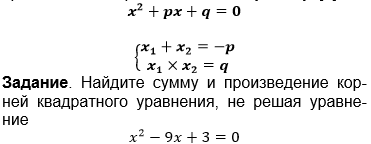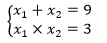Развитие креативности школьников на уроках математики / Открытый урок

Наше время – это время перемен и глобализации. Поэтому становится весьма важным, что, выйдя из стен школы в большой мир, молодые люди должны быть адаптированы к этому миру. К сожалению, в современной российской системе образования господствующим остаётся подход к обучению, как к усвоению определённой суммы знаний. Очень часто обучение сводится к запоминанию и воспроизведению приёмов, действий, типовых способов решения заданий, к усвоению знаний, умений, навыков. А ведь требования современной ситуации таковы, что простого обладания суммой знаний недостаточно, необходима постоянная готовность к меняющимся условиям проблемной ситуации и умение рассмотреть её с разных точек зрения, найти наиболее рациональный способ решения. Вот почему развитие творческой способности должно стать краеугольным камнем системы образования, должно целью реализации различных образовательных программ. Такие программы должны содержать специальные задания, которые способствовали бы активизации творческих способностей, общих для самых разных видов деятельности. Кроме того, чем больше мы предоставляем детям возможностей для конструктивного творчества, тем более вероятным становится их позитивное самоопределение в процессе формирования их личностных качеств [1].

Ведущее место в новой креативной системе образования принадлежит овладению современной методологией творчества ТРИЗ (автор Г. Альтшуллер), как эффективным средством развития творческого мышления, способности генерировать новые нестандартные идеи, как средством творческого саморазвития и воспитания ее духовно-нравственного и волевого комплексов. В этой связи на любом образовательном уровне учащийся из объекта обучения (каким он был при традиционном образовании) становится, прежде всего, субъектом развития, саморазвития и самовоспитания [2, 3].

При проведении уроков необходимо учитывать следующие принципы:

Принцип открытости заданий, который означает, что большинство упражнений предлагают не один, а несколько вариантов решений;
Обогащение познавательного пространства самыми разнообразными предметами и стимулами;
Предоставление детям возможности активно задавать вопросы, познавательной активности в целом;
Помощь детям в выражении их идей;
Уважительное отношение к идеям участников обсуждения;
Создание безопасной психологической атмосферы;
Избегание неодобрительной оценки творческих идей ребёнка, проявление сочувствия к неудачам;
Использование личного примера, ведущего творческого подхода к решению проблем;
Возможность самостоятельного поиска решений

Тема урока: «Теорема Виета».

Цели урока:

- знакомство с теоремой Виета и ее применение для решения квадратных уравнений;

- формирование навыков исследовательской деятельности;

- развитие коммуникативных и познавательных способностей.

1. Мотивация.

Для повторения материала прошлого урока, учитель вызывает ученика к доске и просит записать общий вид квадратного уравнения и приведенного квадратного уравнения.

Учитель

Учащиеся

Чем отличается полное квадратное уравнение от приведенного квадратного уравнения?

Т.е. старший коэффициент равен 1

Запишите формулу, по которой можно найти корни полного квадратного

уравнения

Каждый раз нужно пользоваться этими формулами?

Ученики пытаются вспомнить что-то из теоремы Виета и затрудняются ответить.

2. Содержательная часть.

Учитель

Учащиеся

Учитель дает задание учащимся .

Решите 5 уравнений, записанных на доске, и заполните таблицу следующего вида

№	p	q
1
2
3
4
5

Какого вида квадратные уравнения вам даны?

Учитель контролирует работу учащихся и вызывает к доске 1 ученика, который заполняет таблицу

По таблице найдите связь между корнями уравнения и коэффициентами

Учащиеся решают следующие уравнения:

Приведенные квадратные уравнения вида

№	p	q
1	3	-4	-4	1
2	5	6	-3	-2
3	-5	6	2	3
4	-1	-12	4	-3
5	7	-8	-8	1

Учащиеся замечают, что p равно сумме корней с противоположным знаком, а qравно произведению корней.

Это наглядно видно из следующих таблиц:

p
3	-3
5	-5
-5	5
-1	1
7	-7

q
-4	-4
6	6
6	6
-12	-12
-8	-8

Итак, почему мой вопрос вызвал у вас затруднение?

Т.е. мы получили, что сумма корней является числом, противоположным второму коэффициенту, а произведение – свободному члену.

Какие случаи мы рассматривали? Общие или частные?

Какое утверждение в общем виде мы можем записать.

А как называют эти формулы?

Итак, мы сформулировали тему сегодняшнего урока, а цели наши каковы?

Потому что раньше мы не решали квадратные уравнения другими способами, а теперь выявили зависимость корней от коэффициентов уравнения.

Частные.

Вызывается ученик, который записывает формулы на доске

Теоремой Виета.

Мы должны доказать эту теорему и научиться применять при решении квадратных уравнений.

Но это только предположение наше – это гипотеза.

А гипотезы надо доказывать.

Как?

Что такое корень уравнения?

Что здесь известное и что неизвестное?

Что делать?

Что можно сказать про q?

Какое заключение можно сделать?

Это значение неизвестного, при котором уравнение обращается в верное равенство.

p и q – неизвестные переменные.

Надо решить систему уравнений методом вычитания одного уравнения из другого.

Получаем:

Произведение корней квадратного уравнения равно свободному члену, а сумма корней равна второму коэффициенту с противоположным знаком.

С какими уравнениями мы работали сегодня?

Запишем в тетрадь:

Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение – равно свободному члену. [4]

С приведенными.

Ученик решает у доски:

По теореме Виета:

Ответ. 9;3.

Выполнить письменно:

Является ли число

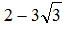корнем уравнения:

х² – 4х – 23 = 0

3. Психологическая разгрузка

Активируем «Кнопки мозга» – выполняется стоя или сидя. Для начала мысленно проведем линию ото лба к носу, подбородку и ниже – она разделяет тело на правую и левую половины. Движения, пересекающие эту линию, интегрируют работу полушарий мозга. Поэтому «Перекрестные шаги» способствуют развитию координации и ориентации в пространстве, делают более успешными приобретение навыков чтения, письма, слушания, усвоения новой информации. А еще снимают боль в пояснице и подтягивают мышцы живота.

- Ноги стоят удобно, параллельно друг другу. Если вы стоите, то колени расслаблены. Одна рука кладется на пупок. Пальцы другой руки прикасаются к двум точкам, расположенным под ключицами между первым и вторым ребром, таким образом, что большой палец оказывается на одной точке, а средний – на другой.

- Далее слегка массируем эти точки пальцами. Рука на пупке просто спокойно лежит.

- Меняем руки и повторяем упражнение, по 30Х30 секунд.

- Выполнение упражнения «Кнопки мозга» способствует обогащению мозга кислородом, за счет этого улучшается восприятие информации.

4. Головоломка

Какой из приведенных ниже вариантов может продолжить логическую последовательность?

5. КИП

С помощью программы PASCAL составьте программу, которая решает квадратные уравнения с помощью теоремы Виета, и проверьте на ней все уравнения сегодняшнего урока.

6. Рефлексия деятельности.

Учитель

Учащиеся

Что нового вы узнали на уроке?

Что можно определить с её помощью?

С помощью теоремы Виета можно определить знаки корней. Каким образом?

Кому понравился урок похлопайте в ладоши…

Теорему Виета.

Найти корни уравнения, их сумму и произведение.

Домашнее задание: последний вопрос остается на дом, №1064, №1045 [4].

Ссылки на источники

Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: Прикладной курс научного творчества: Учебное пособие. - Киров: АНОО «Межрегиональный ЦИТО», 2013. - 212 с
Утёмов В. В., Зиновкина М. М. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ // Концепт. – 2013. – Современные научные исследования. Выпуск 1. – ART 53572. – URL: http://e-koncept.ru/2013/53572.htm. – Гос. рег. Эл No ФС 77-49965. – ISSN 2304-120X.
Горев П.М., Утёмов В. В. Научное творчество: практическое руководство по развитию креативного мышления: Учебно-методическое пособие. – Книжный дом "ЛИБРОКОМ", 2014. – 112 с.
Алгебра. 8 класс, Макарычев Ю.Н., Миндюк Н.Г. и др., издательство «Просвещение», 2010 г.

Скачать публикацию

Развитие креативности школьников на уроках математики

Свидетельство

Похожие публикации