Эффективное решение нестандартных творческих задач детьми младшего школьного возраста

На сегодняшний день для нас представляет профессиональный интерес изучение особенностей развития интеллектуальных способностей младших школьников. Наше общество находится в постоянном развитии, следовательно, через систему образования выдвигает и реализует всё новые требования к человеку, обладающему обучаемостью, то есть способностью к постоянному самообразованию; интеллектуально и физически развитому, что может обеспечить доступ к технологиям только интеллектуально развитым личностям и креативностью или способностью мыслить и действовать творчески [1].

Развитие интеллектуальных способностей – важнейшая задача начального образования, ведь этот процесс пронизывает все этапы развития личности ребёнка, пробуждает инициативу и самостоятельность принимаемых решений, привычку к свободному самовыражению, уверенность в себе [2].

Развивая интеллектуальные способности у младших школьников, вырабатываем у них навыки и умения с интересом, продуктивно трудиться, способность к творчеству. Творчество – не всплеск эмоций, оно неотделимо от знаний, умений. Эмоции сопровождают творчество, увлекают ребёнка, придают ему силы.

Интеллектуальное развитие происходит не само по себе, а в результате многостороннего взаимодействия ребёнка с другими людьми: в общении, в деятельности и, в частности, в учебной деятельности. Пассивное восприятие и усвоение нового не могут быть опорой прочных знаний. Поэтому наша задача – развитие интеллектуальных способностей учащихся, вовлечение их в активную деятельность. Для этого очень важно создать в начальной школе условия для полноценного развития детей, сформировать у них устойчивые познавательные процессы, развивать умения и навыки мыслительной деятельности, самостоятельность в поисках способов решения задач.

В качестве критериев интеллектуального, умственного развития выступают:

самостоятельность мышления, быстрота и прочность усвоения учебного материала, быстрота ориентировки при решении нестандартных задач, умение отличить существенное от несущественного, различный уровень аналитико-синтетической деятельности, критичность ума.

Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в методической литературе, в объяснительных записках к учебным программам. Однако, как это делать, учитель не всегда знает. Нередко это приводит к тому, что интеллектуальное развитие в значительной мере идет стихийно, поэтому большинство учащихся, даже старшеклассников, не овладевает начальными приемами логического мышления (анализ, сравнение, синтез, абстрагирование и др.) Роль математики в развитии логического мышления исключительно велика. Причина столь исключительной роли математики в том, что это самая теоретическая наука из всех изучаемых в школе. В ней высокий уровень абстракции и в ней наиболее естественным способом изложения знаний является способ восхождения от абстрактного к конкретному. Как показывает опыт, в младшем школьном возрасте одним из эффективных способов интеллектуального развития является решение нестандартных задач.

«Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения», – считает Л. М. Фридман. Нестандартная задача (задание) – это учебная задача, содержание которой не укладывается в общепринятые типы и варианты расчётных и экспериментальных задач, имеющая необычную формулировку, с зашифрованным в тексте вопросом, и обеспечивающая адаптацию учащихся в окружающем мире.

Анализ литературы и собственный педагогический опыт позволил выделить следующие критерии принадлежности задач к группе нестандартных:

• неуточненная формулировка условия задачи, при решении которой учащимся необходимо увидеть главное, что невозможно без творческого подхода;
• кажущаяся противоречивость условия, связанная с поверхностным восприятием и существующими у учащихся стереотипами, преодоление которых развивает логическое мышление и придаёт решению нестандартный характер;
• многоплановость условия, допускающая присутствие в задаче сложных взаимосвязей между отдельными компонентами, глубина понимания, сущности которых во многом определяет уровень предположений учащихся;
• многовариантность решения;
• многоуровневость решения, выдаваемая различным уровнем сложности. Первый уровень решения исключает глубокое осмысление условия. Следующие уровни требуют от учащегося большего интеллектуального потенциала и предполагают решение, основанное на подробном теоретическом обосновании;
• интегрированность содержания, когда обсуждаемая в задачах тематика относится к области литературы, искусства, техники, экологии, быта и других разделов материальной культуры и требует для решения теоретических знаний ряда смежных дисциплин;
• познавательность. Текст задачи содержит интересную информацию;
• отсутствие алгоритма решения.

Нестандартные задачи в курсе математики не имеют общих правил. Процесс решения нестандартных задач состоит в последовательном применении двух основных операций:

• сведения путём преобразования или переформулировки нестандартной задачи к стандартной;
• разбиение нестандартных задач на несколько стандартных подзадач.

Трудность таких задач обусловлена тем, что они требуют проведения дополнительных исследований и рассмотрения различных вариантов. Здесь не нужны знания теории, выходящие за рамки программы, нужны умения думать, мыслить, догадываться, соображать [3].

Анализ методической и специальной литературы показал, что до настоящего времени не существует определенной классификации нестандартных задач. И это не случайно, так как практически невозможно определить единый признак – основание для классификации таких задач.

Нестандартные задания по математике, используемые в начальной школе, условно можно разделить на следующие классы: задачи на установление взаимно-однозначного соответствия; задачи о лжецах; задачи, решаемые с помощью логических выводов; задачи о переправах; задачи о переливаниях; задачи о взвешиваниях.

Наблюдения показывают, что даже при решении несложных нестандартных задач, учащиеся много времени тратят на рассуждения о том, за что взяться, с чего начать. Чтобы помочь учащимся найти путь к решению задачи, мы должны поставить себя на место решающего, попытаться увидеть и понять источник его возможных затруднений. Наша помощь, оставляющая различную долю самостоятельной работы, позволит ученикам развивать творческие способности, накопить опыт, который в дальнейшем поможет находить путь решения новых задач.

Вот несколько методов решения: алгебраический; арифметический; графический; практический; метод предположения; метод перебора.

Они могут применяться при решении нестандартных задач.

Опыт показывает, что для развития интеллектуальных способностей необходимо включать в процесс обучения разнообразные виды нестандартных задач (не ограничиваться материалами, предложенными в учебнике).

В процессе обучения действует принцип минимакса. Принцип минимакса заключается в следующем: школа должна предложить ученику содержание образования по максимальному уровню, а ученик обязан усвоить это содержание по минимальному уровню. Слабый ученик ограничится минимумом, а сильный – возьмет все и пойдет дальше. Все остальные разместятся в промежутке между этими двумя уровнями в соответствии со своими способностями и возможностями – они сами выберут свой уровень по своему возможному максимуму. Обучение осуществляется деятельностным методом, когда дети не получают знания в готовом виде, а «открывают» их в процессе самостоятельной исследовательской деятельности. Учитель предлагает учащимся систему вопросов и заданий, подводящих их к самостоятельному «открытию» нового свойства или отношения.

Известно несколько различных способов решения логических задач. Давайте назовем их так: способ рассуждений; способ таблиц; способ графов; способ бильярда; способ кругов Эйлера [4].

Охарактеризуем кратко эти способы.

Способ рассуждений – самый примитивный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.

Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

В этом разделе рассматривается еще один тип логических задач. Это задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости, а также задачи, связанные с операцией взвешивания на чашечных весах. Простейший прием решения задач этого класса состоит в переборе возможных вариантов. Понятно, что такой метод решения не совсем удачный, в нем трудно выделить какой-либо общий подход к решению других подобных задач.

Эффективность обучения младших школьников решению нестандартных задач зависит от нескольких условий:

• Задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся.
• Необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке, вернуться к началу и искать другой, верный путь решения.
• Нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач.

На первом этапе учащиеся должны:

• усвоить процесс решения любой задачи (читаю задачу, выделяю, что известно и что надо узнать);
• познакомиться с приемами работы над задачей (виды наглядной интерпретации, поиска решения, проверки решения задачи и др.)

На втором этапе учащиеся применяют ранее сформулированные общие приемы в ходе самостоятельного поиска конкретных задач.

Вывод: при поиске решения незнакомой задачи полезно сделать чертеж (рисунок), т.к. он может быть способом решения задачи.

Для успешного обучения учащихся решению нестандартных задач должны быть сформированы три составляющих мышления:

• высокий уровень элементарных мыслительных операций: анализа, синтеза, сравнения, обобщения, классификации и др.;
• высокий уровень активности, раскованности мышления;
• высокий уровень организованности и целенаправленности.

Если работу по формированию у детей логических умений и навыков, необходимых в любой интеллектуальной деятельности, проводить систематически не только на уроках, но и во внеурочной работе, то можно наблюдать повышение интеллектуально-творческий потенциал учащихся, мотивации к обучению, создание ситуации успеха.

Систематическое выполнение целенаправленно подобранных нестандартных задач влияет на развитие мыслительных процессов младших школьников и ведёт к повышению качества знаний. Работа по развитию творческих способностей оказывает положительное влияние на качество знаний учащихся по математике: повышается уровень математического образования младших школьников, развивается интерес к предмету, познавательная активность в обучении [5].

Нестандартные задачи – важная составляющая задачного подхода.

Используемые в обучении школьников нестандартные задачи классифицируются для каждого предмета естественнонаучного цикла.

Рассмотрим использование нестандартных способов решения, которые подразумевают новый, необычный подход в обучении на различных предметах, в том числе, на уроках русского языка и литературного чтения.

На уроке литературного чтения в 1 классе в учебнике «Букварь»дети встречаются с множеством непонятных слов, требующих пояснения: чабан, кортик, рапира, пирога, фрегат, флагшток, вестовые, клокотал, Осака, Курск, Канары, Ниагара, Миссисипи, калмыки, мордва, коми, шест, шесток, шествовать… Среди этого многообразия слов географические названия, названия народностей, населяющих просторы России, словарные слова. Проблема непонимания смысла слов привела к поиску новых приёмов. Одним из наиболее действенных приёмов критического мышления является работа со словарной картой, удовлетворяющей всем требованиям эффективного обучения [6].

Работа со словарной картой способствует пополнению словарного запаса и должна стать неотъемлемой частью нашей повседневной работы на каждом уроке и дома. Важно культивировать этот интерес, объяснить детям и их родителям, как работать со словарными картами. В ходе домашнего и самостоятельного чтения дети находят незнакомые для себя слова, вспоминают, что знают об этом слове и расширяют эти знания, используя контекст, словари, подбирая антоним, выводят собственное (то есть осознанное и усвоенное) значение слова. Тщательная работа над каждым новым словом должна вестись постоянно, непрерывно расширяться и носить самостоятельный характер.

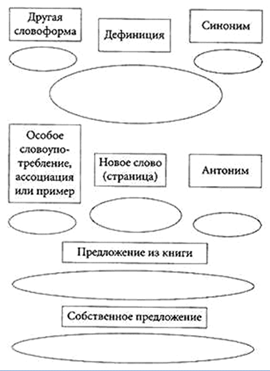
Для успешного усвоения новых слов нужно, чтобы обучаемые являлись активными, заинтересованными участниками процесса.

В связи с этим хочется поделиться историей про слово сад.

На уроке русского языка перед изучением темы «Однокоренные слова» в первом классе я пригласила детей на «прогулку» по необычному саду, в котором растут слова. На слайдах презентации были изображены деревья, пели птицы. Каждый слайд знакомил с новыми словами, которые выросли из слова «сад»: садовник, садовод, садовый, посадит. В глазах детей был интерес, и у одного ребёнка возник вопрос: «А в словосочетании детский сад слово имеет такое же значение?» Детям было предложено найти об этом информацию. Вместе с родителями ребёнок нашёл информацию не только о родстве слов, но и о фразеологизме «голова садовая». Возникший интерес привёл ребёнка к маленькому исследованию, получению знания самостоятельно. В этом и заключается задача учителя – пробудить интерес ребёнка к слову. Можно просто ответить: «Да, смысл слов одинаков» и на этом исчерпать тему, а можно превратить этот интерес в маленькое, но собственное открытие! Так приходит глубинное понимание слова. Психологи говорят о понимании как о процессе, при котором«поверхностная структура преобразуется в глубинную», а так же характеризуют понимание как многоступенчатый, многогранный и многомерный процесс. Понимание не придёт к человеку, если не проанализировать прочитанное, глубокое понимание теснейшим образом связано с мыслительными навыками высшего порядка: анализом, синтезом, оценкой. Понимание глубинного смысла слова связано с использованием особых стратегий, обучающих методов и приёмов такого типа мышления, как критическое. Нужны нестандартные подходы в работе над словом. В нестандартности упражнений из кинезиологии, в различных приёмах критического мышления есть что-то необычно, что пробуждает и поддерживает интерес детей!

Хочется рассказать об использовании на уроках русского языка нестандартных приёмов работы над словарными словами. Примером послужила фраза про слово карандаш, которая пропевалась на мотив песни «Учкудук – три колодца» «Это кара-кара-кара-кара-кара-карандаш!». «Об этом я прочла в маленькой статье журнала «Начальная школа». Автор статьи привела этот пример, и он остался в памяти. Пропела эту песенку детям и поняла, что подобный приём действует: в словарном диктанте в слове карандаш из всего класса только двое детей допустили ошибки. Затем «придумалась» фраза «На КАМе-КАМыши», «МАК-МАК-МАКар любит МАК и МАКароны», «ТОП, ТОП, ТОПаетТОПор, чтобы порубить дрова, во двор» (на мелодию «Топ, топ, топает малыш» ), «МАртышкаМАришка поехала в МАрте на МАшине в МАгазин за МАлиной», «КАП-КАП-КАП-КАПуста, КАП-КАП-КАПитан, КАП-КАП-КАП-КАПуста, КАП-КАП-КАПюшон», «ГОРОжанеГОРОдилиОГОРОд», «СОРОке – сорок лет». Попевки мы сопровождаем различными движениями рук, тела, что помогает запомнить слово на другом уровне, ведь тело тоже способно запоминать».

Решение нестандартных задач является одним из средств развития интеллектуальных способностей младших школьников. Необходимо стремиться к тому, чтобы учащиеся испытывали радость от решения трудной для себя задачи [7].

Эффективное решение нестандартных творческих задач детьми младшего школьного возраста также осуществляется на занятиях курса «Загадки природы» Юшкова Алексея Николаевича. Практика работы с детьми младшего школьного возраста в рамках этого курса ориентирована на развитие у младших школьников предметных компетенций (позиция наблюдателя, исследовательская позиция) и сквозных (ключевых) компетентностей – образовательной самостоятельности, образовательной инициативы и интегральной компетентности – умения учиться. Сейчас все эти образовательные качества зафиксированы как значимые в государственном стандарте начального образования [8].

Курс «Загадки природы» (1–4 классы) направлен на развитие у детей:

• вопросительности, как детской способности обнаруживать странное и необычное в знакомых явлениях природы и жизни животных организмов, и как исходного условия – возникновения мышления, в том числе и «теоретического» (естественнонаучного);
• позиции участника диалога, когда дети в совместном обсуждении того или иного явления природы, задавая вопросы друг другу, предлагая собственные версии объяснений странного поведения обсуждаемого объекта, начинают понимать основания собственных высказываний, основания высказываний других сверстников, совместно выходят на новое понимание обсуждаемого объекта;
• предметной осведомлённости как результата групповой и самостоятельной работы с массивами информации. Наличие собственных вопросов обеспечивает осмысленность поиска и освоение информации;
• позиции наблюдателя и исследователя, как принципиального условия возникновения субъекта теоретического мышления;
• позиции экспериментатора (конец 3-го, четвёртый классы) как познавательной установки на прояснение (проверку) собственных гипотез инструментальными средствами.

В первом и втором классах в рамках курса «Загадки природы» для нас принципиально важно:

• Поддержать и развить детскую чувствительность к феномену разнообразного движения живых организмов, как одной из основ возникновения вопросов познавательного характера. Например, «Вспомните, как устроены Драконы и Змеи Горынычи. Как летают эти змеи? Они могут скользить по воздуху и парить как планеры? Покажи, как летают драконы», «Сделайте Землемера (гусеница-пяденица из сказки В. Бианки) из бумажной трубки. Нарисуйте ему глазки, пририсуйте лапки. Изобразите его движение», «Лягушка прыгает, отталкиваясь от земли. Изобразите это. Может ли она с силой оттолкнуться от гладкого льда?».
• Развить детскую учебную вопросительность, выводя её в область проблем и загадок окружающего мира. Например: «Лягушка ловит комаров при помощи своего липкого языка. Какие вопросы возникают в связи с этим?», «Щука может неподвижно «висеть» среди водорослей в толще воды. Какие вопросы по этому поводу можно задать друг другу?», «О чём вы можете спросить друг друга, глядя на жилища этих животных (рисунки жилищ животных – воздушный колокол паука-серебрянки, гнездо рыбы-колюшки, птицы-ткачика, гнездо вороны)».
• Расширить детскую осведомлённость о мире живой и неживой природы с обязательным предоставлением возможности самому ребёнку разбираться в этой информации, искать её, экспериментировать, строить совместные личностно значимые описания объектов, явлений, событий. Например: «Центр равновесия (тяжести) у самолёта из спичек должен находиться примерно посередине. Для чего?», «На болоте живёт растение-хищник. Называется оно — росянка. Кто что об этом знает? Что об этом пишут в Интернете?», «Как в Интернете можно найти видео с полётом божьих коровок?».
• Поддержать и развить детские интуиции, позволяющие им «позади» наблюдаемого эпизода (явления природы, поведения живого организма) чувствовать элементы научной системы (С. И. Гессен). Например: «Крокодилов относят к большой группе животных, которые называются «пресмыкающиеся», Кто догадается, почему?», «Вспомните по одному волшебному превращению и по одному настоящему. Нарисуйте эти превращения. Бывают ли превращения в жизни лягушек и бабочек? Превращения и изменения – в чём разница?».
• Поддержать и развить способности детей первого и второго классов к выстраиванию собственных гипотез о явлениях природы и к диалогу по поводу странностей жизни животных и явлений природы. Например: «У кромки воды повстречались морские и сухопутные улитки. Кто кем из вас будет? О чём вы спросите друг друга?», «Божьи коровки могут взбираться вверх по гладкому стеклу. Как им это удаётся? Придумайте свои версии. Задайте друг другу вопросы», «Кусочек сахара растворяется в воде и становится невидимым. Что потом происходит с этими невидимыми частичками? Предложите свои версии. Задайте друг другу вопросы».
• Оформить исследовательскую позицию у школьников первых двух лет обучения как на принципиально знакомом им материале, так и на новом. Например: «Какие силы есть у волшебных предметов из волшебных сказок? Как об этом можно узнать-догадаться, если о силе и свойствах этих предметов, например, «шапки-невидимки» или «ковра-самолёта» вам никто ничего не сказал?», «Какую роль в движении рыб играют грудные плавники и хвостовой плавник в момент движения рыбы по прямой; когда она тормозит; в то время когда она «стоит на месте», когда поворачивается?».

В третьем-четвертом классах в рамках курса «Загадки природы» для нас принципиально важно:

• Поддерживать и развивать способности младших школьников 3–4 классов к выстраиванию собственных гипотез о явлениях природы и к диалогу по поводу странностей жизни животных и явлений природы. Например: «У кромки воды повстречались морские и сухопутные ежи. О чем вы спросите друг друга?», «Как узнать, для чего нужна та или иная часть тела живому организму? Какое оборудование потребуется для таких исследований? Помогут ли в этом исследователям – океанариумы, террариумы, зоопарки?», «Все видели, как божьи коровки могут ползать не только по стенам, но и по стеклу. А мухи могут ползать и по потолку. Понять, как насекомым удается передвигаться по вертикальным стенам и даже «вверх ногами» – это путь к созданию машин, «умеющих» то же самое. Предложите свои версии строения лап мух, позволяющих им быстро передвигаться «вверх ногами».
• Обеспечить дальнейшее развитие детской учебной вопросительности, выводя ее в область вопросов, фиксирующих проблемность объекта обсуждения.

Отметим, что среди детских учебных вопросов могут быть выделены следующие группы:

Во-первых, это вопросы на уточнения, по принципу «А как у вас это происходит\случается\выглядит и пр.».

Во-вторых, это большая группа вопросов-противопоставлений.

• это вопросы, в которых нечто в объекте противопоставляется человеку (его анатомии, морфологии, поведению и пр.);
• это вопросы, в которых нечто в объекте противопоставляется типичному представителю класса этих объектов;

В третьих, это вопросы, в которых проблематизируется, например, способ жизни объекта, но с точки зрения «человеческой безопасности и пр.». Эти вопросы более сложно устроены по сравнению с предыдущим типом вопросов, т.к. здесь не просто противопоставление, а «контекстная проблематизация».

В четвертых, это вопросы-противоречия. В этих вопросах фиксируется внутреннее противоречие исследуемого (обсуждаемого) объекта. Эти вопросы (массово) возникают позже вопросов-противопоставлений; ближе к концу 3-го класса, но при условии систематической работы по организации диалогических ситуаций между школьниками. Примеры этих вопросов: «Как из жидкого яйца появляется твердый цыпленок?», «Как корень растения впитывает воду, ведь корень плотный?».

Учитель: «Ребята, мы с вами, сейчас, рассмотрим капли воды под микроскопом. Надо будет зарисовать, что вы увидели».

Дети рисуют в альбомах и на доске.

Учитель: «Теперь рассмотрите, как выглядит под микроскопом лёд, и тоже зарисуйте».

Учитель: «Вы нарисовали воду в виде маленьких шариков. Представьте, что вы – маленькие шарообразные человечки. Изобразите капли воды».

Учитель: «Теперь изобразите лёд».

Учитель: «Ребята, как из воды получаются снежинки, ведь вода, замерзая, превращается в лед?».

С подобными вопросами дети уже уходят с урока. И с этими вопросами они уже должны обращаться к физикам, химикам, биологам, инженерам.

Для детей открывается мир науки, мир ученых-профессионалов, мир разных областей знаний. У них оформляются собственные интересы, они впервые начинают думать о профессиональном выборе, о будущей профессии.

И наша работа с детьми в течение четырех лет начальной школы должна им в этом помочь.

Девизом для развития креативности и раскрытия творческого потенциала у детей младшего школьного возрастав обучении могут служить слова выдающегося немецкого драматурга и философа Лессинга: «Спорьте, заблуждайтесь, ошибайтесь, но ради бога, размышляйте, и хотя и криво, да сами».

1. Полякова А. Г. Модернизация структуры экономического пространства региона // Вестник Череповецкого государственного университета. – 2011. – Т. 2. № 2–30. ­­– С. 28–31.

2. Вахновецкий Б. А. Логическая математика для младших школьников. – Москва: «Новый учебник», 2004.

3. Левитас Г. Г. Нестандартные задачи в курсе математики начальной школы. – «Начальная школа», 2001 г. № 5, с. 61-67.

4. Талызина Н. Ф. Формирование познавательной деятельности младших школьников. – Москва: Просвещение, 1988.

5. Мухина В. С. Детская психология. – Москва: ООО «Апрель Пресс», ЗАО Издательство ЭКСМО-Пресс, 2000.

6. Винокурова Н. К. Развитие творческих способностей учащихся. – Москва: Образовательный центр «Педагогический поиск», 1999.

7. Утёмов В. В., Зиновкина М. М. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ // Концепт. – 2013. – Современные научные исследования. Выпуск 1. –ART 53572. – URL: http://e-koncept.ru/2013/53572.htm. – Гос. рег. Эл No ФС 77-49965. – ISSN 2304-120X.

8. Юшков А. Н. Познавательный интерес и собственное дело детей. – Санкт-Петербург: АНПО «Школьная лига», 2013.

 

Abstract. The article discusses effective methods for solving non-standard creative tasks of children of primary school age which are used by teachers of  the municipal Autonomous educational institution «Gymnasium №77» on various educational subjects. The authors describe adapted methods of scientific creativity, describes the various methods of solving creative tasks.

Key words: problems of open type, creative tasks, the development of creativity, creative potential.