Адаптированные методы научного творчества в обучении ментальной арифметике

В федеральных и региональных документах, таких как Федеральном государственном образовательном стандарте основного общего образования, утверждённом приказом № 1897 Министерства образования и науки Российской Федерации 17 декабря 2010 г. [1], указах, постановлениях, распоряжениях и иных нормативно-правовых актах по школьному образованию отражена необходимость развития личности с широким интеллектуальным потенциалом, способствующим развитию креативности как основы инновационной деятельности. Достигать данные цели можно только комплексно и системно. Одно из решений этой задачи – использование методов научного творчества в обучении детей [5].

В статье разобран пример использования теории решения изобретательских задач (ТРИЗ) Г. С. Альтшуллера, как дополнительного обучения детей, занимающихся ментальной арифметикой. Структура креативного урока по системе НФТМ-ТРИЗ М. М. Зиновкиной отличается от обычного (традиционного), включает в себя блоки, реализующие задачи занятия, советующие целям креативного образования в целом [2, 3].

1. Блок мотивации. Решение задач – задача не простая. Нужно приложить много усилий, чтобы решить сложную, хорошую задачу. Сильные «решатели» справляются со сложными задачами, а сверхсильные – находят универсальные принципы, откуда потом складываются теории. И для таких решений требуются креативные личности. Но возникает вопрос, что мы понимаем под словом креативность. Каждый день мы слышим это слово – креативное решение, креативный подход, креативные идеи. И как измеряется эта креативность? В определении слова, каждый будет прав отчасти. Под креативностью мы будем понимать способность человека к творчеству, способность создавать что- то оригинальное, казалось бы, в стандартной ситуации [5].

Ежедневно мы решаем очень много различных ситуаций. Ребёнок с малых лет уже начинает решать задачи. Конечно, это не только математические, но и жизненные задачи (бытовые). Мы стараемся найти наиболее эффективный путь, а иногда движемся по пути психологической инерции (Крейнин Сима [4]). Но знать решение всех возможных проблем, которые приключатся с нами в жизни, мы не можем.

Подсчитать сколько задач человек решает за свою жизнь практически невозможно. Только в школе ученик решает порядка 10 000 задач (и это только по школьным предметам). А в целом за жизнь выйдет миллион различных ситуаций, которые нам надо преодолеть. Если мы будем искать алгоритм решения каждой такой ситуации, то на это уйдёт вся жизнь.

Было бы очень хорошо уметь решать все задачи с помощью одного механизма. Возникла перед нами ситуация, а у нас сразу решение появилось. Конечно, такого алгоритма нет. Но, методы и приемы, которые помогают нам ускорить процесс нахождения решения проблемы, есть. наша задача в рамках дополнительных заданий – научить детей пользоваться этими методами.

2. Блок творческого разогрева. Ученикам выдаётся изображение клякс. Все разбиваются на пары. Задача каждой группы назвать как можно больше вещей на что похоже данное изображение. Оценивается оригинальность идей.

Часто решая задачи, мы используем самые легкие пути их решения, перебирая все возможные. Данные способ решения называется «метод проб и ошибок». Из начального условия задачи, мы начинаем двигаться во все направления, в поиске решения, но эффективным и верным может быть только несколько направлений [5].

3. Теоретический блок 1. Рассмотрим рис 1. В первой ситуации (а) перебирая все возможные варианты решения задачи, мы так и не приближаемся к её решению. В ситуации (б) Мы находимся ближе к решению задачи, но её точного решения так и не достигаем. В ситуации (в) мы используем системный подход и решение становится уже ближе, но снова пришлось перебрать много вариантов. В ситуации (г) мы от задачи идём сразу к решению по одному пути [5].

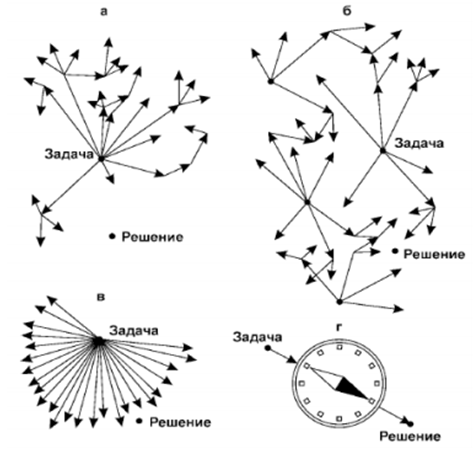Рис. 1. Типы мышления

Трудность приближения к 4 типу решения задач создаёт психическая инерция (ПИ). Под психологической инерцией понимают предрасположенность к какому-либо типу решения проблем, при этом игнорируются все другие способы решения. И проблема заключается в том, что человек находится «в плену» данного мышления. Уже начиная со школы, ученики могут из раза в раз использовать одни и тот же алгоритм, хотя он не является эффективным, а иногда даже отрицательным.

Психологическая инерция бывает различных видов, приведём некоторые её примеры.

Инерция привычной функции и функциональной направленности. Данный тип инерции подразумевает, что мы используем предмет только по прямой, привычной функции. Например, стул – только для того что бы сидеть. Но если его рассмотреть, то мы можем найти большое количество способов его применения.

Инерция привычной формы, привычного внешнего вида. Какой бы формой не обладал предмет, по мере её усовершенствования форма будет меняться. Нет ничего постоянного. Когда мы ищем новое решение, нам необходимо изменять форму объекта. При изменении геометрии объекта, мы будем получать совершенно новые, эффективные решения задачи.

Инерция несуществующего запрета. Эти запреты могут исходить со внешний стороны, а также исходить со стороны того, кто решает задачу. Эти запреты связаны с общепринятым мнением.

4. Практический блок 1. Для выявления психической инерции можно использовать специальные загадки. Детям они очень нравятся, но использовать их можно только 1 раз, далее они не имеют такого эффекта.

Примеры загадок:

– Кто при Екатерине Великой ходил вверх головой? (дети отвечают – шуты)

(Ответ – все)

– Сколько кубометров земли содержится в яме размерами: глубина 2 м, ширина 4 м, длина 5м? (дети стараются вспомнить все свои математические знания, или просто дают ответ наугад)

(Ответ – 0, в яме нет земли)

– На столе стоят две лампы: керосиновая и газовая. Что вам надо зажечь прежде всего? (здесь ответы у детей разделяются, но снова они пытаются отгадать)

(Ответ – спичку, прежде чем зажечь лампу, нужно прежде всего зажечь спичку.)

После данных и других загадок, ученики понимают, что психологическая инерция в нашем мышлении присутствует. Следующим шагом идёт обсуждение ситуаций, в которых проявляется данное явление. Например, когда мы несколько раз пытаемся открыть дверь опуская ручку вниз, а на самом деле ручка поднимается вверх; или после нескольких примеров на вычитание продолжаем вычитать, хотя в примере стоит знак «плюс». Ученики приводят примеры из своей жизни.

Так психологическая инерция – это плохо? И нам нужно от неё полностью избавляться? Не всегда. Она помогает нам выполнять привычные действия (чистить зубы, кушать, завязывать шнурки) не обдумывая каждый шаг. Получается, психологическая инерция облегчает выполнение действий, но начинает мешать, когда у нас появляется задача придумать что-то новое, непривычное для нас.

Одним из способов борьбы с ПИ – упражнение «думай по-другому». Ученики разбиваются на группы по 3 человека. Им даётся высказывание, на которое мы все однозначно ответим да, но их задача придумать как можно больше вариантов, когда мы ответим «нет».

Примеры вопросов:

– В воде всегда мокро?

– На калькуляторе считать быстрее чем в уме?

– Днём всегда светло?

– Машина всегда обгонит человека?

Все ответы детей выслушиваются и записываются, потом находятся самые оригинальные идеи.

Все идеи можно выстроить по уровням оригинальности.

5. Психологическая разгрузка. Отдохнуть от умственной нагрузки и переключиться детям помогают упражнения с мячиками для большого тенниса. Упражнения начинаются от самых простых – подбрасывание одного мячика двумя руками поочерёдно, до жонглирования тремя мячами. Данные упражнения развивают крупную моторику и координацию движений.

6. Теоретический блок 2. Ранее мы упомянули о методе проб и ошибок, и психологической инерции. Это два способа мышления, которыми мы пользуемся ежедневно.

В 20 веке появилась потребность в решении большого количества задач, причём эти решения должны были быть эффективными. В результате стали появляться новые способы. Такие как, «мозговой штурм», «синектика», «морфологический анализ», «метод контрольных вопросов». Одна из проблем использования данных методов – необходимость креативно мыслить.

Тогда возникает закономерный вопрос, все ли люди обладают креативным мышлением? Является ли это природным задатком или его можно развивать? Конечно, данное мышление можно и нужно развивать. Оно полезно, как в повседневной жизни, как школьном обучение, так и взрослым людям на работе.

Данное направление называется РТВ (развитие творческого мышления). Существует несколько приемов – «метод фокальных объектов» «фантограммы Альтшуллера».

7. Практический блок 2. На уроке с детьми используется «метод фокальных объектов». Как уже упоминалось ранее, этот метод помогает развивать креативное мышление, а также находить очень интересные идеи. Название появилось потому что предмет, который мы будем усовершенствовать берётся в «фокус» рассмотрения.

Структура метода представлена на (рис. 2). Опишем его подобротнее.

– Берём фокальный объект, то есть предмет, который нужно усовершенствовать (например, рюкзак)

– Берём несколько различных объектов. Лучше если они будут из различных сфер жизни. Можно их придумывать самим, или брать из книг и журналов. Это должны быть существительные. (например, градусник, дуб, мяч)

– Выделяются признаки и свойства выбранных объектов. Для этого необходимо задать вопрос «этот объект какой?» и «этот объект что делает?». (например, градусник –длинный, стеклянный, легкий, меряет температуру)

– Выделенные признаки переносятся на выбранный нами изначально объект. (например – длинный рюкзак, лёгкий рюкзак, рюкзак который меряет температуру)

– С помощью ассоциаций происходит дальнейшее развитие придуманных вариантов. (например, рюкзак который меряет температуру – в нём может располагаться термоотдел, который сможет сохранять температуру продуктов)

– Оценка полученных результатов и выбор наиболее удачных.

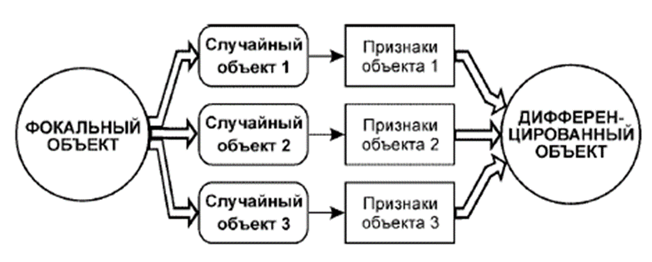Рис. 2. Метод фокальных объектов

8. Головоломка. Работа с учениками продался посредством решения «квадратов Никитина». Детям выдаются детали квадратов. Необходимо перемещая их друг относительно друга собрать квадрат. Если у ребёнка возникает сложность, ему выдаётся квадрат-рамка. Эта головоломка тоже помогает бороться с ПИ.

9. Теоретический блок 3. Что бы развивать в детях навыки «решателя» и видеть задачу «насквозь», необходимо развивать функциональное мышление. Функциональное мышление – умение думать упорядоченно. Это помогает увидеть самую суть задачи и решать её по шагам заданного алгоритма. Данный тип мышления помогает понять ребёнку, что в мире всё взаимосвязано; видеть интересные задачи, а не преграды; уверенно действовать; думать последовательно и логично.

10. Практический блок 3. Для перехода к функциональному мышлению необходимо узнать несколько определений и понять их механизм взаимодействия (рис. 3).

Инструмент – тот объект, который совершает работу (предмет-труженик).

Изделие – то, на что воздействует инструмент.

Функция – работа инструмента, которая направлена на изменение изделия

Очень важно понять определение функции. На первый взгляд цель и функция очень похожие определения. Но различие в них есть. Цель - это мысленное предугадывание события, а функция - это действие, воплощающее цель. Таким образом, функция - это то, что необходимо людям, это способность изделия обеспечить какое-то потребительское свойство.

Для обозначения функции удобно использовать список специальных глаголов:

- Перемещать.

- Удерживать.

- Пачкать.

- Деформировать.

- Направлять.

- Разделять, отделять.

- Информировать.

- Управлять.

- Передавать.

- Нагревать.

- Охлаждать.

- Соединять.

Хорошим упражнением для закрепления данной темы будет обсуждение с детьми какими функциями обладают окружающие их предметы.

Исследуя механизм взаимодействия предметов. Мы заметим, что не только инструмент воздействует на изделие, но существует и обратная связь

Как так вышло? Дело в том, что когда инструмент воздействует на изделие (молоток перемещает гвоздь), он совершает свою прямую функцию. Но в это же самое время изделие тоже действует на инструмент (гвоздь царапает молоток) – только уже это функция обратная. Заметим, что одно из действий в этой связке всегда полезное, а второе – вредное.

Как только ребёнок начинает видеть данные взаимосвязи, сразу становится понятно какие задачи и проблемы появляются перед решателем.

11 блок. Заключение. На этом наши блоки дополнительных уроков завершаются. Данные занятия помогают более детально усваивать детьми, как и общее, так и дополнительное образовательные программы.

Ссылки на источники: