Цели и задачи урока:
- способствовать формированию творческой личности учащихся;
- преодолевать инерцию мышления;
- учить находить площадь многоугольников, применять эти навыки в бытовых ситуациях.
Ход урока
Блок 1. Мотивация («Встреча с чудом»)[1,2]
- Ребята! Предлагаю вам рассмотреть необычные картинки! [3]


- На что вы обратили внимание?
- Эти картинки не анимированные, они статичные, но когда мы начинаем рассматривать их, то нам кажется, что они движутся. Это похоже на настоящее чудо! Как вы думаете, за счёт чего достигается такой эффект?
Блок 2. Содержательная часть программы курса.
- Сегодня мы вспомним, как находится площадь прямоугольника, а также будем учиться находить площадь некоторых многоугольников.
1) - Перед вами на столах лежат фигуры.
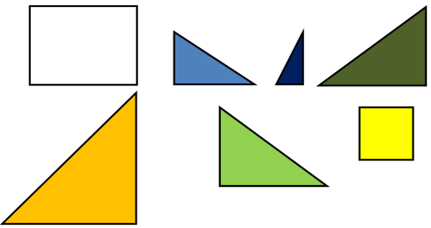

- Выберите среди них те, которые являются прямоугольниками. Как найти их площадь? (Измерить стороны, умножить длину на ширину.) Запишите вычисления в тетрадь.
- Как называются остальные фигуры? (треугольники)
- Чем они похожи между собой? (у них один из углов прямой)
- Теперь найдите площадь самого большого прямоугольного треугольника (детям даётся время для размышления и соответствующих действий).
- Каким способом вы это делали?
Выслушиваются ответы детей. Возможны следующие варианты ответов: разбить каждый треугольник на квадратные сантиметры, пересчитать количество полных квадратиков и добавить половину неполных квадратных сантиметров, получим приближённое значение площади; каждый прямоугольный треугольник представляет собой половину прямоугольника, поэтому можно измерить стороны треугольника, образующие прямой угол, перемножить их и полученное произведение разделить на два и т.п.
- Какое из этих предложений вам показалось наиболее удобным и точным? (площадь прямоугольного треугольника равна половине площади прямоугольника)
- Найдите площади оставшихся прямоугольных треугольников. Запишите соответствующие вычисления.
2) - Из имеющихся у вас фигур постарайтесь сложить другие фигуры. Подумайте, как найти их площадь.
Возможные варианты:
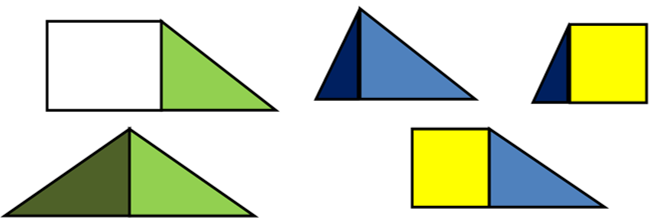

- Как называются составленные вами фигуры?
- Чему равна площадь каждой из них?
3) – Догадайтесь, а как можно найти площадь таких фигур? (раздаётся второй набор фигур)


Ребята выполняют необходимые измерения, построения, вычисления. После завершения работы объясняют свои действия.
Блок 3. Психологическая разгрузка (физические упражнения выполняются в группах примерно по 8 человек). На этом этапе урока необходимо некоторое свободное пространство.
- Ребята! Возьмитесь за руки. По моему сигналу постарайтесь образовать указанную геометрическую фигуру. (Учитель называет различные фигуры (квадрат, окружность, треугольник, прямоугольник, трапеция). Дети, не отпуская рук друг друга, стараются выполнить упражнение.)
Блок 4. Головоломка.
- Переложите четыре спички из шестнадцати, чтобы получилось три квадрата [4].
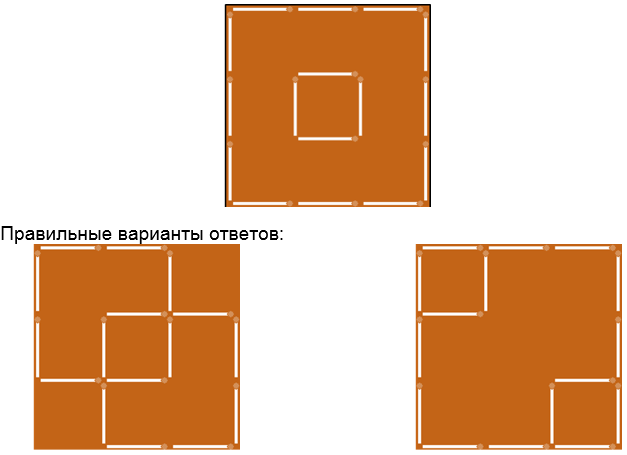

Перерыв
Блок 5. Интеллектуальная разминка.
- Предлагаю вам решить такие задачи [5]:
1) Усталый охотник
Морозной тёмной февральской ночью усталый охотник возвратился домой в свою хижину, Почти две недели он ходил по лесам, проверяя капканы. В хижине у него была керосиновая лампа, очаг и дровяная печурка, но у охотника осталась всего одна спичка. Как по-вашему, что он зажжёт сначала? (Сначала охотник зажжёт спичку.)
2) Отдых за столом
Однажды на отдыхе за круглым столом оказались пятеро ребят родом из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алеша, Коля и Витя. Москвич сидел между томичом и Витей, санкт-петербуржец – между Юрой и Толей, а напротив него сидели пермяк и Алеша. Коля никогда не был в Санкт-Петербурге, а Юра не бывал в Москве и Томске, а томич с Толей регулярно переписываются. Определите, в каком городе живет каждый из ребят.
Ответ: Толя живет в Москве, Витя – в Санкт-Петербурге, Юра – в Новгороде, Коля – в Перми, а Алеша – в Томске.
Блок 6. Содержательная часть (начало).
- В нашей газете неоднократно писалось о том, что надо сделать так, чтобы наш город был чище и красивее. Начать можно со своего двора, с площадки рядом с подъездом; убрать мусор, разбить небольшую клумбу или посадить красиво цветущий кустарник. Нам на школьном дворе выделили небольшой участок, который вы можете увидеть, посмотрев в окно. План участка изображен на доске. Давайте подумаем, что можно с ним сделать и что для этого необходимо.
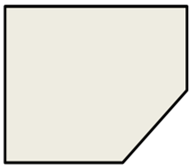

Дети высказывают свои предложения по созданию клумбы: надо вскопать землю, высадить рассаду цветов. Для этого необходимо найти площадь данного участка; продумать план посадки цветов; рассчитать, какое количество рассады необходимо согласно этому плану; закупить достаточное количество рассады.
- Каким образом вы будете вычислять площадь участка?
Скорее всего, дети предложат разбить данную фигуру на прямоугольники и прямоугольный треугольник, найти и сложить площади полученных фигур. Также могут поступить и другие предложения. Все они выслушиваются и оцениваются, принимая во внимание их рациональность.
Далее учитель сообщает, что необходимые измерения были произведены и получены следующие результаты:
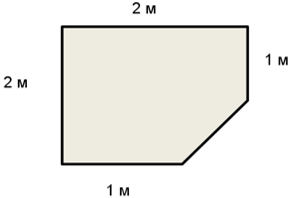

Детям предлагается произвести необходимые вычисления и найти площадь участка.
- Чтобы наша клумба была нарядной и красивой, давайте засадим её «ковром» цветов. Рассаду можно купить в торфяных горшочках, диаметр которых 10 см. Сколько таких горшочков нам понадобится? (Ученики просчитывают, какое максимальное количество рассады им потребуется.)
- Для того чтобы клумба выглядела аккуратно и красиво, сначала надо продумать, в каком порядке мы будем сажать цветы. Имеется возможность приобрести рассаду цветов жёлтого, белого, красного и синего цвета. Сейчас каждый из вас нарисует свой план рассадки растений при помощи компьютера.
Блок 7. Компьютерная интеллектуальная поддержка.
Дети переходят к компьютерам. У каждого на экране компьютера план участка. Маленький квадратик соответствует месту для посадки одного цветка. Выполняя заливку квадратиков, учащиеся создают план посадки растений.
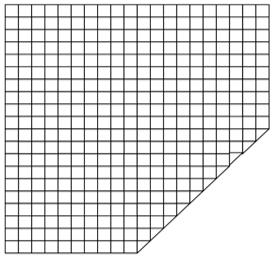

У каждого ребёнка получится свой узор. Например, такой:
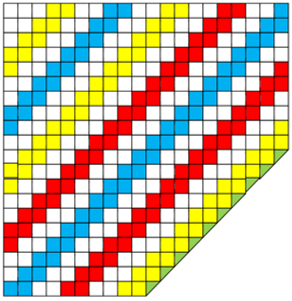

Блок 6. Содержательная часть (продолжение).
- У вас получились очень красивые клумбы. Нам с вами осталось просчитать, сколько денег придётся затратить, чтобы воплотить в жизнь ваш проект. Рассада стоит: белые цветы – 25 рублей за 1 шт., жёлтые – 28 р., красные – 30 р., синие – 31 рубль.
- Посчитайте, пожалуйста, затраты, согласно вашему плану размещения цветов.
- Сколько потребуется комплексного удобрения для подкормки рассады из расчёта 10 г на 1 м²?
Блок 8. Резюме.
- Ребята! Давайте вспомним, что интересного было на нашем уроке?
- Что вам понравилось больше всего?
- Вам бы хотелось, чтобы на нашем школьном дворе появилась такая клумба, какую вы сегодня спроектировали?
- Закройте глаза. Поднимите, пожалуйста, руку те, кому понравился наш сегодняшний урок!
- А теперь поднимите руку, кому он не понравился!
- Мне тоже очень понравилось с вами вместе работать! До свидания!
Замечание. Данный урок можно провести и в более старших классах. В этом случае можно дать более сложные расчёты и вычисления. Дети могут засаживать клумбу цветами не сплошным «ковром», а некоторые участки – газонной травой, засыпать цветной галькой и т. д., то есть представляется большой простор для творчества.
Ссылки на источники
- Зиновкина М. М., Утёмов В. В. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ // Современные научные исследования. Выпуск 1. – Концепт. – 2013. – ART 53572. – URL: http://e-koncept.ru/article/964/ – Гос. рег. Эл № ФС 77 – 49965. – ISSN 2304-120X.
- Утёмов В. В. Адаптированные методы научного творчества в обучении математике // Концепт: научно-методический электронный журнал. – 2012. – № 7 (июль). – ART 12095. – 0,5 п. л. – URL: http://www.covenok.ru/koncept/2012/12095.htm. – Гос. рег. Эл № ФС 77-49965. – ISSN 2304-120X.
- Оптические иллюзии: картинки – http://konstantinsmirnov.ru/wpcontent/uploads/2012/07/no_gifs_just_image_illusions_01.jpg
- «Энциклопедия головоломок» – 2007-2009 – htpp:// www.spravko.info/sp_01.html
Kozlova Nina Anatolevna,
teacher MAOU Gymnasium No. 6, t. Krasnoarmeisk Moscow region
nina.coz@yandex.ru
Methodological development of the polygon Area.
Annotation. The article focuses on developing activities for class 5, representing the dual creative lesson. Its structure follows the author's pedagogical system of M. M. Zinovkina´s in the TRIZ-NFTM. This development can also be used for optional classes in mathematics.
Keywords: TRIZ, creative NFTM-lesson, the formation of a creative personality.
