Формирование универсальных учебных действий обучающихся на уроках математики

В последние десятилетия произошло коренное переосмысление целей и ценностей современного образования. Логика развития общества привела к осознанию того, что истинное совершенствование жизни связано не только с внешней образованностью человека, усвоением им той или иной системы знаний и умений, сколько с развитием его ума и способностей, системы ценностей и мотивационных установок [1].

Развитие личности в системе образования обеспечивается прежде всего через формирование универсальных учебных действий, которые являются инвариантной основой образовательного и воспитательного процесса. Овладение учащимися универсальными учебными действиями создаёт возможность самостоятельного успешного усвоения новых знаний, умений и компетентностей, включая организацию усвоения, т. е. умения учиться [2].

Поэтому важнейшей задачей современной системы образования является формирование универсальных учебных действий (УУД), обеспечивающих школьникам способность к саморазвитию и самосовершенствованию. Решение этой задачи должно идти путем сознательного и активного присвоения обучающимися нового социального опыта, а не только освоение учащимися конкретных предметных знаний и навыков, которые успешно реализуются в процессе обучения математике. При этом знания, умения и навыки рассматриваются как производные от соответствующих видов целенаправленных действий, так как они порождаются, применяются и сохраняются в тесной связи с активными действиями самих учащихся.

В связи с этим, основная цель, которая стоит передо мной, как учителя математики – научить детей самостоятельно добывать знания. А для этого необходимо: создавать образовательную среду обучающихся на основе системно-деятельностного подхода, создавать условия для развития познавательной активности обучающихся через использование в работе инновационных приемов и методов.

Формирование любых умений, в том числе и УУД проходит через следующие этапы:

1. Первичный опыт выполнения УУД и мотивация.
2. Освоение того как это УУД надо выполнять.
3. Тренинг, самоконтроль и коррекция.
4. Контроль [1].

Виды универсальных учебных действий (рис. 1):

Рис. 1. Виды универсальных учебных действий

Регулятивные учебные действия обеспечивают возможность управления познавательной и учебной деятельностью посредством постановки целей, планирования, контроля, коррекции своих действий, оценки успешности усвоения. 

Личностные действия позволяют сделать учение осмысленным, увязывая его с реальными жизненными целями и ситуациями. Личностные действия направлены на осознание, исследование и принятие жизненных ценностей, позволяют сориентироваться в нравственных нормах и правилах, выработать свою жизненную позицию в отношении мира. 

Познавательные действия включают действия исследования, поиска, отбора и структурирования необходимой информации, моделирование изучаемого содержания. 

Коммуникативные действия обеспечивают возможности сотрудничества: умение слышать, слушать и понимать партнера, планировать и согласованно выполнять совместную деятельность, распределять роли, взаимно контролировать действия друг друга, уметь договариваться, вести дискуссию, правильно выражать свои мысли, оказывать поддержку друг другу и эффективно сотрудничать как с учителем, так и со сверстниками. 

Универсальные учебные действия у обучающихся на уроках математики формируются путем вовлечения детей в активный процесс изучения математики. Ключевой точкой в образовании становится опыт деятельности ребенка.

Проектирование заданий (формулировки заданий) в соответствии с развиваемыми УУД на уроках математики:

Познавательные УУД

1. Найти соответствие: (определение, рисунок, формула)
2. Дан список слов, формул, символов, рисунков и т. д. Какое из них лишнее и почему?
3. Дан список слов, терминов, формул, рисунков и т. д. Подчеркнуть те, которые относятся к …
4. Заполнить таблицу данными из текста.
5. Классифицировать список понятий, группу рисунков, символов, указать критерии классификации.
6. Найти сходство или отличия между А и Б (термины, объекты, рисунки, системы, процессы), выдели ведущие характеристики для сравнения в определенной ситуации.
7. Заполнить сравнительную таблицу.
8. Свернуть текст в опорный конспект, шпаргалку.
9. Представить текстовую информацию в виде таблицы, графика, схемы.
10. Составить кроссворд с данными словами.
11. Ответить на вопросы и записать только цифры (числовой диктант).
12. Продолжить ряд или вставить пропущенный фрагмент.
13. Даны первое и последнее предложение (с понятиями темы), написать связный рассказ, эссе.
14. Доказать правильность решения.

Коммуникативные УУД

1. Найти в тексте смысловые ошибки и прокомментировать их.
2. Ответить на вопросы по тексту.
3. Выполнить какое-либо действие (например, сократить дробь). Сформулировать и записать правило.
4. Прочитать текст, описывающий опыт, эксперимент, реальный или мысленный, сформулировать главную мысль, сделать и объяснить вывод.
5. Составить подписи к кроссвордам.
6. Сформулировать определения для новых понятий.
7. Загадать понятия прилагательными, глаголами.
8. Составить вопросы по изученному материалу для использования в конкретной ситуации.
9. Дописать предложения, чтобы утверждения стали верными.
10. Решить задачу, объяснить свое решение.

Регулятивные УУД

1. Решить компетентностную задачу: применить знания в реальной ситуации, на практике. Вопросы в задаче: можешь ли ты, имеет ли смысл, как можно объяснить, стоит ли и т. д.
2. Дана задача. Необходимо установить и записать последовательность действий при решении задачи. Объяснить.
3. Лабораторная работа. Прочитать список действий, необходимых для выполнения данной работы. Порядок действий изменен. Необходимо восстановить правильный порядок действий, записать их и выполнить работу.
4. Составить план устного ответа на конкретный вопрос.
5. Выбрать из нескольких алгоритмов самый эффективный, доказать свое мнение.
6. Найти, в чем заключается ошибка в каждом утверждении, записать правильно.
7. Определить главные действия и их порядок (из числа предложенных) при решении задачи, построении графика и т. д.
8. Обоснование верности какого-либо утверждения.
9. Расставить предложения текста в нужном порядке так, чтобы получилось доказательство теоремы
10. Построить систему понятий или интеллект-карту для решения какой-либо проблемы.

Личностные УУД

1. 1.Составить или решить задачу в содержании которой используются исторические факты, имена известных людей прославивших нашу Родину.
2. Решение задач с практическим содержанием.
3. Создание учебных ситуаций, требующих самооценивания и оценивания учебной деятельности сверстников.
4. В конце урока организация рефлексии учащимися своего отношения к учению, его результатам, самому себе как «продукту» учебной деятельности.

1) Оцените свои ответы на уроке. На уроке я:
а) ответил(а) по просьбе учителя, но ответ неправильный;
б) ….,ответ правильный;
в) ответил(а) по своей инициативе, но ответ неправильный;
г)…, ответ правильный;
д) не ответил(а).
2) Продолжите высказывание.
а) У меня получилось… б) Меня удивило… в) Теперь я умею…
3) Продолжите высказывания.
а) Знания, полученные на уроке, мне необходимы…
б) Я получил(а) полезную информацию о том, что…
4) Продолжите высказывание:
а) Мне понравился сегодняшний урок, но…
б) Для меня материал урока: 1) трудный, вот если бы…; 2) легкий , и я….
Основным подходом формирования УУД, согласно новым Стандартам, является системно-деятельностный подход.
Одним из методов (возможно наиболее эффективным) реализации данного подхода является проектно-исследовательская деятельность. Работа над проектом позволяет формировать и развивать одновременно все УУД.
Пример социального проекта.
Тема: «Ремонт классного кабинета»
Заказчик: учитель математики
Цель проекта: развитие учебной, коммуникативной и социальной компетенций обучающихся.
Задачи, решаемые в процессе работы над проектом:
1. Формирование у обучающихся умения переноса математических знаний в новую ситуацию.
2. Формирование представления о практической значимости математических знаний.
3. Развитие умения работать в группе.
План работы.
1. Провести измерительные работы в кабинете.
2. Сделать необходимые вычисления.
3. Узнать стоимость строительных материалов и инструментов.
4. Выполнить необходимые расчёты.
После завершения проекта учащиеся смогут пользоваться языком геометрии для описания предметов окружающего мира; вычислять значения геометрических величин (площадей)решать несложные практические расчетные задачи, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера. 

Формирование УУД

Личностных УУД:
- Формирование позитивной самооценки, самоуважения, самоопределения
- Воспитание целеустремлённости и настойчивости.
Коммуникативных УУД:
- Умение вести диалог, координировать свои действия с партнёром.
- Способность доброжелательно и чутко относиться к людям, сопереживать.
- Умение выступать перед аудиторией, высказывать своё мнение, отстаивать свою точку зрения.
Регулятивных УУД:
- Умение самостоятельно и совместно планировать деятельность и сотрудничество, принимать решения.
- Формирование навыков организации рабочего пространства и рационального использования времени.
Познавательных УУД
- Сбор, систематизация, хранение, использование информации.

Примеры заданий по математике, формирующие
универсальные учебные действия

Личностные УУД
Цель: патриотическое воспитание, отношение к социальным ценностям: формирование интереса к культуре и истории родной страны; осознание себя членом общества; мотивация учения - развитие интереса к математике, положительное отношение к процессу познания.
1.Зашифрованное письмо
Расшифруйте стихи о национальной особенности нашей Родины. Как вы понимаете данные строки? Кто их автор?
19 15 11 15 . 12 11 20 20 2 21 . 13 8 . 14 11 13 23 16 18 .
4 12 17 2 13 11 15 . 11 3 22 2 15 . 13 8 . 2 9 15 8 12 2 16 18 .
19 . 13 8 7 . 11 20 11 3 8 13 13 4 23 . 20 16 4 16 18 .
5 . 12 11 20 20 2 21 . 15 1 6 13 11 . 16 11 10 18 1 11 . 5 8 12 2 16 18.
Ключ к разгадыванию
1)  14, 10, 21, 20 - математический знак
2)  16, 19 , 14, 11, 7 - вид угла
3)  17, 8, 20, 16, 18 – число граней прямоугольного параллелепипеда
4)  3, 11, 1, 11, 5, 4, 23 - сторона равнобедренного треугольника
5)  4, 1, 20, 2, 11, 15, 4 – утверждение, принимаемое без доказательства
6)  11, 16, 12, 8, 9, 11, 1 - медиана
7)  20, 8, 1, 19, 22, 4, 23 - прямая, пересекающая параллельные прямые
8)  13, 4, 10, 11, 6, 8, 13, 2, 8 - метод сравнения плоских фигур
(Ответ: Умом Россию не понять
Аршином общим не измерить
У ней особенная стать –
В Россию можно только верить. Ф. Тютчев)
2. Соедини буквы в слово
Смоленщина богата великими людьми. Выполнив задания теста, вы узнаете фамилию нашего знаменитого земляка.
ТЕСТ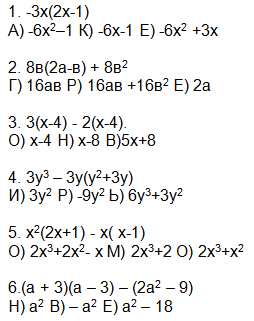 

Рис. 2. Ответ на задание. Егоров

Михаи́л Алексе́евич Его́ров (5 мая 1923 – 20 июня 1975) – Герой Советского Союза, сержант Красной Армии, вместе с младшим сержантом М. В. Кантария водрузили Знамя Победы на крыше немецкого Рейхстага рано утром 1 мая 1945 года.
Родился в крестьянской семье в деревне Ермошенки; Руднянского района Смоленской области.
За совершённый подвиг ему Указом Президиума Верховного Совета СССР от 8 мая 1946 года было присвоено звание Героя Советского Союза с вручением Ордена Ленина и медали Золотая Звезда .
Похоронен в городе Смоленске у крепостной стены в Сквере Памяти Героев.
Его именем названы улица в Смоленске и переулок в посёлке Монастырщина Смоленской области. Почётный гражданин Смоленска.
В родном городе Рудня дом, где жил Герой Советского Союза, переоборудован в дом-музей. В музее собраны различные вещи, ранее принадлежавшие герою.

Регулятивные УУД
Цель: сформулировать учебную проблему, составить план и последовательность выполнения работы; формировать умение соотносить свои действия с планируемыми результатами; осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований
1. Восстанови правильный порядок действий.
Учащийся должен восстановить алгоритм решения рационального уравнения, в котором левая или правая части уравнения рациональные выражения и решить данное уравнение.
1) Найти область допустимых значений переменной (ОДЗ) уравнения (при каких значениях переменной знаменатель обращается в нуль) нулю.
2) Проверить, какие из полученных корней удовлетворяют ОДЗ; те которые не входят в ОДЗ являются посторонними корнями.
3) Домножаем обе части данного уравнения на общий знаменатель и к каждой дроби записываем дополнительные множители, т. е. те множители, которых нет в данном знаменателе, но есть в общем знаменателе
4) Перенести из правой части уравнения все данные в левую и приравнять к
5) Найти общий знаменатель (О.З.) данных дробей
(выписать знаменатель одной из дробей, лучше самый большой, и к нему дописать те множители, которых нет в этом знаменателе)
6) Записать ответ
7) Решаем целое уравнение, выполнив соответствующие преобразования (раскрыть скобки, привести подобные слагаемые, с переменной собрать в левой части уравнения, без переменной в правой части уравнения и решить полученное линейное уравнение)
8) Разложить знаменатели данных дробей на множители (если это необходимо) с помощью:
– вынесения общего множителя за скобки;
– формул сокращенного умножения:
9) Записываем целое уравнение, полученное из произведения числителей на их дополнительные множители (без знаменателя).
Если учащиеся не могут справиться с заданием, то им можно предложить уравнение, которое уже решено по данному алгоритму. Учащиеся анализирую решение и восстанавливают алгоритм.

2. Помоги другу.
Задание № 1. Решите задачу, составив план действия.
На столе стоит пузырек с надписью «Выпей меня!». «Это же яд», - подумала Алиса, выпила  его содержимого и выросла до 200 см. Какую часть жидкости ей надо еще выпить, чтобы стать трехметрового роста?
Задание № 2. Выполните действия по порядку и расшифруйте фамилию известной детской писательницы.

 

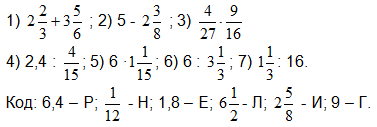
Задание № 3.
Расположите дроби в порядке возрастания, и вы узнаете имя одного из героев автора, фамилию которого вы вспомнили, решив задание № 2:

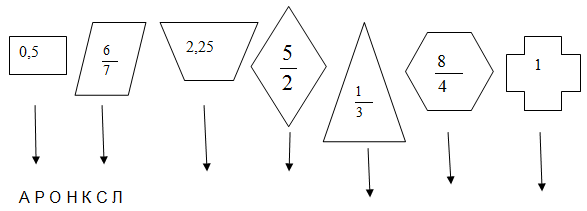
Познавательные УУД
Цель: формировать умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы.
1. Задачи «ПРОВОЦИРУЮЩИЕ» учащихся на ошибку. Первые две задачи решаются хорошо, а вот в третьей можно допустить ошибку, если не знаешь теоремы о площади треугольника.
1) Вычислите площадь треугольника, у которого АВ = 6 см, ВС = 4 см, ˂АВС = 30˚.
2) В равнобедренном треугольнике боковая сторона равна 12 см, а угол при вершине 60˚. Найдите площадь треугольника.
3) В треугольнике АВС АВ = ВС = 8 см, , ˂ВАС = 30˚. Вычислите площадь треугольника
2. Задачи с недостающими данными
1) Площадь футбольного поля равна 750 м2 . Найдите его ширину.
2) Сколько надо обоев, чтобы оклеить стену в комнате длиной 6 м.
3. Сделай выбор
Цель: выявление способности отделять существенные признаки предметов и явлений от несущественных.
Инструкция: В каждом ряду одно слово стоит перед скобками, а далее в скобках следуют пять слов, имеющих отношение к первому слову. Необходимо выбрать всего два слова, которые имеют наибольшую связь со словами перед скобками.
1. Куб (углы, чертеж, камень, сторона, дерево).
2. Деление (класс, делимое, карандаш, делитель, бумага).
3. Кольцо (алмаз, диаметр, проба, золото, окружность).
4. Патриотизм (город, родина, друзья, семья, человек).
5. Книга (рисунки, рассказ, бумага, оглавление, текст).
6. Пример (буква, числа, скобки, знаки арифметических действий, ответ).
7. Угол (отрезок, точка, луч, прямая, фигура).
4. Аналогия
Инструкция: Даны три слова. Подумайте, как связаны первые два из них и укажите в списке четвертое слово, которое точно так же связано с третьим.
1. УМЕНЬШАЕМОЕ - РАЗНОСТЬ
МНОЖИТЕЛЬ - ?
2. САНТИМЕТР – МИЛЛИМЕТР
ГЕКТАР - ?
3. КВАДРАТ – ПРЯМОУГОЛЬНИК
КУБ - ?
5. Докажите, истинны или ложны следующие утверждения
1. Каждое натуральное число имеет не менее двух делителей.
2. 12 – делитель 6.
3. Если первое число является делителем второго числа, то второе число кратно первому.
4. Каждое из натуральных чисел, кратных 7, служит делителем 42.
5. Число 24 имеет всего 5 делителей.
6. Сумма двузначного и трехзначного чисел, записанных с помощью одной цифры, делится на 3.
7. Цифровой диктант
Верно ли утверждение, определение, свойство? (да – 1, нет – 0)
1. Одночленом называют сумму числовых и буквенных множителей. (-)
2. Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
3. В результате умножения многочлена на многочлен получается многочлен.
4. Произведение нескольких одночленов называется многочленом.(-)
5. В результате умножения одночлена на многочлен получается многочлен.
6. Степенью многочлена стандартного вида называют сумму степеней всех входящих в него одночленов. (-)
7. Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
8. Одночлены, входящие в состав многочлена и имеющие одинаковые числовые множители называют подобными членами многочлена. (-)
(Ответ: 01101010)