Креативный урок математики для учащихся 6-го класса по теме «Простые и составные числа»

Традиционная школа, по мнению Гина, в лучшем случае учит давать правильные ответы. Тогда как для жизни куда важнее уметь правильно ставить вопросы. Каждый ребёнок проходит в раннем детстве этап развития, когда вопросы сыпется из него, как мука из рваного мешка. Но проходит время, и социум подавляет в нём эту активность – так удобнее.

ТРИЗ (теория решения изобретательских задач) – педагогика ставит задачу подготовить человека не к сдаче академического экзамена (это пожалуйста, заодно), а к жизни. Тем более, что «жизнь похожа на урок алгебры. Как только вы решите одну задачу, учитель задаёт следующую» [1].

ТРИЗ-педагогика вводит знания через творческую деятельность, преимущественно через решение открытых задач. При этом если ребёнок решает задачу не так, как ожидает от него учитель, то это является, при условии действительного решения, только дополнительным плюсом для этого ребёнка. Отец вырвал из журнала страницу с картой мира, порвал на куски и дал сыну: «Я свожу тебя в зоопарк, если ты соберёшь карту». Через 10 минут карта была собрана. – Как? – удивился отец? – Папа, а на другой стороне был рисунок человека, я собрал его из кусочков, и на этой стороне получилась карта [1].

ТРИЗ-педагогика через открытые задачи объединяет познание мира в единое целое, демонстрирует неразрывность разных предметных знаний; считает креативность важнейшей составляющей современной личности. Креативность можно и нужно развивать. ТРИЗ-педагогика считает ученика субъектом образования. Ценно то знание, которое добывается осознанно, в творческой деятельности, самостоятельными усилиями [1].

Всё дело в том, что в ТРИЗ разработаны определённые алгоритмы, по которым решаются задачи. То есть решение открытой, творческой задачи происходит не «как получится», а по заданной процедуре. Это не гарантирует успешного решения задачи, но повышает вероятность решения и позволяет планировать шаги, последовательность и время решения.

Алгоритмы классической ТРИЗ – это сложные и многоходовые инструменты, которые требуют особого навыка и определённых умений для работы с ними. Для подростков мы предлагаем упрощённый инструмент – ПРИЗ (процедура решения изобретательских задач).

На этом шаге предлагается прочитать условие задачи, сформулировать его своими словами и записать в традиционной форме:

• Дано: …
• Найти (объяснить): …

Если школьникам кажется, что они могут дать ответ сразу, пусть запишут свою гипотезу (идею) и продолжат решение задачи по ПРИЗу – скорее всего, они смогут выдвинуть и другие гипотезы.

Здесь школьникам предлагается проанализировать условие задачи и ответить на следующие вопросы:

Если на этом шаге возникли какие-то гипотезы, их нужно записать. Отметим, что на этом шаге не следует спешить решать задачу, так как главная цель шага – как можно лучше осмыслить условие задачи.

Рекомендуется подумать, как перечисленные ниже явления могли бы способствовать получению необходимого в условии задачи результата?

Список явлений:

• механические;
• акустические;
• тепловые;
• электрические;
• магнитные;
• электромагнитные (оптические);
• ядерные;
• химические;
• биологические;
• социальные.

Данный шаг – главный для выдвижения гипотез. Учитель объясняет, что на этом шаге не нужно быть слишком критичными, так как следует постараться наработать максимум гипотез. Отметим, что в процессе решения иногда возникают 1–2 идеи, а иногда и более 10.

На этом шаге школьники отбирают из выдвинутых гипотез наиболее правдоподобные и расставляют их в порядке убывания правдоподобности. Если школьникам не удалось сформулировать правдоподобные гипотезы, то можно рекомендовать глубже изучить условие задачи, а также поискать дополнительные справочные материалы. После этого стоит пройти шаги ПРИЗа ещё раз, причём постараться сделать это более внимательно.

На этом заключительном шаге школьники должны предложить эксперименты, в том числе мысленные, по проверке каждой правдоподобной идеи (гипотезы) или выполнить соответствующие расчёты. ПРИЗ учит мыслить структурно – это его главная задача. [1]

Учитель должен побуждать ребенка находить противоречия в том или ином явлении и разрешать. Разрешение противоречий – это важный этап мыслительной деятельности ребенка.  Использование приемов активации деятельности школьников способствует развитию творческого воображения. Приведу некоторые свои приёмы активизации интереса к изучению математики.

1. Математический бой. Класс разбивается на 4 команды. Каждая команда получает задание. Обсуждение решения проходит в команде. Разыгрывается последовательность игры (какая команда с кем играет). Команда соперников вызывает на решение задачи № … из другой команды. Команда имеет право отказаться от решения, тогда баллы достаются команде, которая вызвала. Любая команда может ответить на нерешенную задачу. Начисляются дополнительные баллы.

2. Проектная и исследовательская работа. Данный вид работ имеет возможность развивать творческий потенциал учащихся. Участвовать в различных конкурсах. Для более сильных учеников можно использовать ПРИЗ-технологию.

3. Счастливый случай. Игра проводится на последнем уроке четверти. Актуализируются знания учащихся. Используются задания на развитие образного воображения, творческого мышления (придумать продолжение истории).

4. Продолжи…Найди закономерность и продолжи числовой или буквенный ряд. Дети находят от 10 до 15 закономерностей.

Приведу пример урока математики в 6 классе, разработанного в структуре «креативный урок». Тема урока «Простые и составные числа». УМК – авторы А. Г. Мерзляк, В. Б. Полонский.

Личностные: формировать умения представлять результат своей деятельности, объективно оценивать труд одноклассников.

Предметные: сформировать понятие простого и составного числа; научить раскладывать натуральное число на простые множители.

Метапредметные: формировать умения определять понятия, создавать обобщения.

Учащийся научится определять, составным или простым числом является данное число; раскладывать составное число на простые множители.

Учитель держит в руках решето (детское сито).

– Здравствуйте, ребята! Сегодня мы совершим открытие. Как вы думаете, зачем мне на уроке математики понадобилось решето? Что можно сделать, используя решето? (Ученики высказывают разные мнения)

В тетрадях запишите: число, классная работа, числа от 2 до 30.Возьмите цветные карандаши и вычеркните все четные числа; числа кратные 3; 5. Какие числа у вас остались? Сколько делителей имеют эти числа? Учащиеся приходят к выводу, что оставшиеся числа имеют только два делителя: единицу и само это число. Что вы сделали с числами? (Зачеркнули, просеяли)

История: Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые. Эратосфен дал таблицу простых чисел до 1000.

Задача 1. Назовите все делители числа: 28;29;30;31.

Задача 2. Какие из чисел 165,106, 207, 253, 271, 282, 305, 315,374, 389 делятся нацело: на 2; на 5; на 3; на 9?

Задача 3. Число 204 равно произведению чисел 34 и 6. Является ли число 34 делителем числа 204? А число 6?

В ходе обсуждения задач 1–3, учащиеся приходят в выводу:

Простые числа имеют только 2 делителя: единицу и само это число;

Составные числа имеют больше 2 делителей.

Как вы думаете, почему определение в учебнике дано для натуральных чисел?

Как вы думаете, сколько делителей имеет 1?

Можно ли 1 отнести к простым числам? К составным?

Учащиеся приходят к выводу, что 1 не относится к простым, ни к составным числам.

105=15*7=35*3=5*21=3*5*7

Любое составное число можно представить в виде произведения простых чисел, т.е. разложить на простые множители.

Если множители в разложении числа повторяются, то их записывают в виде степени.

№104,110 устно; №105,106,113,115 по вариантам (два человека за отворотами доски); №108;111

– Ребята, встаньте, пожалуйста, поднимите руки над головой и покажите, сколько существует простых чисел; составных чисел. (Дети несколько раз выполняют упражнение).

Идет обсуждение задачи по четверкам. Шахматный конь начинает свой маршрут в левом нижнем углу доски, а заканчивает его в правом верхнем углу. Может ли конь при этом побывать на всех полях доски по одному разу? (Не может. После каждого хода изменяется цвет клеточки, на которой стоит конь. Следовательно, после 63-го хода конь должен оказаться на белой клеточке, а правый верхний угол – черный.) После этого высказываются свои решения. Оппоненты проверяют решение и могут не согласиться с решением. Происходит дискуссия. Можно видоизменить задачу. Может ли конь при этом побывать на каждой 2 клетке поля; на 3 клетке?

Задание везде одинаково: зачеркнуть все буквы, встречающиеся более одного раза, а оставшиеся буквы соединить. Какое число получится?

1. ОДИН ДВА ТРИ СТО СОДА РУЛЬ ИВА. (нуль)

2. ВОСЕМЬ ДВА ТРИ СЕМЬ ПАН ТРАП. (один)

3. ДЕВЯТЬ ПЯТЬ РЕПА ЯР. (два)

4. СТО СОРОК ОДИН ДНО КОД. (три)

5. ЛОНО ПЯТНО НОЛЬ. (пять)

6. ТРИ МИР МЫС МЯЧ КИРКА. (тысяча)

Простым или составным является число 11? 11111?

Можно ли продолжить этот ряд? Будет ли он конечным? Ваше мнение.

Работа с учебником стр.26

Разбор задач №119,127,128 с обсуждением и общим решением.

Пример: Класс разбивается на две команды. Каждая команда пишет на своем листочке трехзначное число, которое они загадали. Это должно быть число, цифры которого не повторяются, и первая – не 0.Задача каждого игрока – отгадать число, загаданное противником.

В свой ход игрок называет трёхзначные числа, у которых тоже не повторяются цифры. Второй игрок должен сравнить названное число с тем, что он загадал, и ответить, сколько цифр угадано и стоит на нужном месте, это «быки», а сколько цифр угадано, но стоит не на своём месте. Это – «коровы».

Вот, к примеру, я загадала число 704.

Мой противник называет число 432.

– Одна корова! – отвечаю я ему. Я не сообщаю ему, какая именно из цифр угадана, а только говорю, что она есть, и стоит не на том месте.

357 – спрашивает противник.

Я отвечаю: «снова одна корова!» и не говорю, что корова за это время поменялась.

123 – спрашивает противник.

– Пусто! – отвечаю я, ни одной из этих цифр в моём загаданном числе нет.

Теперь мой противник может, зная, каких цифр в моём загаданном числе точно нет, воспользоваться этим для поиска «коров».

512 – спрашивает он, зная, что ни 1, ни 2 нет в моём числе.

– Пусто!

Из этого можно сделать вывод, что 7 точно есть.

Рассуждая подобным образом, каждый игрок старается выяснить число противника как можно скорее.

Записывать вопросы противника удобно под своим задуманным числом.

Удобно над своими вопросами выписывать все цифры – и отмечать, каких точно нет, и про какие есть какая-то информация.

Если мы за первые 3 хода перепробовали 9 разных цифр, и у нас есть данные только про 2 коровы, то мы можем сделать вывод, что та цифра, которую мы ещё не называли, точно есть!

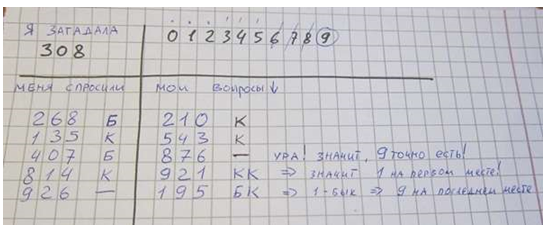
Рассуждая подобным образом, мы можем выяснить число!

Когда логика игры становится понятна, можно играть с четырёхзначными числами или со словами из четырёх не повторяющихся букв. Когда вы начнёте играть со словами, вы поймёте, что придумывать примеры будет намного сложнее.

Электронная версия этой игры находится на сайте http://робомозг.рф/Articles/BullsAndCowsRules

– А теперь, ребята, отложите работы, выпрямите спинки, глубоко вздохните, приведите в порядок свои мысли.

Давайте вспомним, какое натуральное число называют простым? Составным? Почему число 1 не относят ни к простым, ни к составным числам? Существует четное простое число? Назовите наименьшее простое число? Любое ли составное число можно разложить на простые множители?

А теперь посмотрите на экран и закончите предложения:

• Сегодня я узнал(а)…….
• Я удивился(ась)………
• Теперь я умею……….
• Я хотел(а) бы…….

Данный урок способствует формированию творческого мышления и творческих способностей учащихся. Структура креативного урока отличается от традиционной структуры и включает в себя блоки, которые не только соответствуют современным требованиям креативного образования, но и помогают реализовать цели и задачи в обучении математики. Только в процессе целенаправленной, упорной работы удастся сформировать определенные качества и добиться заинтересованности на уроках. Многообразие форм дидактической работы порождает многообразие целевых установок учащихся, увеличивает объем времени, необходимого на самостоятельную работу. Приобретение знаний, умений и навыков самостоятельной работы приучает учащихся к получению нестандартных эффективных решений, развивает творческое мышление; создает предпосылки для их применения в системе профессиональной деятельности, совершенствует способности устного и письменного общения, отдавая предпочтение выражению мнений, эмоций и чувств, а также умению аргументировать. [3, 4] Но по-настоящему творческой личность станет тогда, когда для этого будут созданы все условия: дома, в школе, в общении с друзьями. Дух творчества возникает в том случае, когда у ребенка появляется заинтересованность и желание работать.