Федеральный государственный образовательный стандарт основного общего образования (далее – ФГОС) представляет собой совокупность требований, обязательных при реализации основной образовательной программы основного общего образования образовательными учреждениями, имеющими государственную аккредитацию.
Стандарт включает в себя требования:
- к результатам освоения основной образовательной программы основного общего образования;
- к структуре основной образовательной программы основного общего образования, в том числе требования к соотношению частей основной образовательной программы и их объему, а также к соотношению обязательной части основной образовательной программы и части, формируемой участниками образовательного процесса;
- к условиям реализации основной образовательной программы основного общего образования, в том числе к кадровым, финансовым, материально-техническим и иным условиям.
В основе Стандарта лежит системно-деятельностный подход, который обеспечивает:
– формирование готовности к саморазвитию и непрерывному образованию;
– проектирование и конструирование социальной среды развития обучающихся в системе образования;
– активную учебно-познавательную деятельность обучающихся;
– построение образовательного процесса с учетом индивидуальных возрастных, психологических и физиологических особенностей обучающихся.
В ФГОС основного общего образования содержится характеристика универсальных учебных действий.
Универсальные учебные действия (УУД) – это совокупность действий учащегося, обеспечивающих его культурную идентичность, социальную компетентность, толерантность, способность к самостоятельному усвоению новых знаний и умений, включая организацию этого процесса, а также способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта.
Личностные универсальные учебные действия обеспечивают ценностно-смысловую ориентацию обучающихся (умение соотносить поступки и события с принятыми этическими принципами, знание моральных норм и умение выделить нравственный аспект поведения) и ориентацию в социальных ролях и межличностных отношениях.
Применительно к учебной деятельности следует выделить три вида личностных действий:
– личностное, профессиональное, жизненное самоопределение;
– смыслообразование, т. е. установление обучающимися связи между целью учебной деятельности и её мотивом, другими словами, между результатом учения и тем, что побуждает деятельность, ради чего она осуществляется. Ученик должен задаваться вопросом: какое значение и какой смысл имеет для меня учение? – и уметь на него отвечать.
– нравственно-этическая ориентация, в том числе и оценивание усваиваемого содержания (исходя из социальных и личностных ценностей), обеспечивающее личностный моральный выбор.
Коммуникативные универсальные учебные действия обеспечивают социальную компетентность и учёт позиции других людей, партнёров по общению или деятельности; умение слушать и вступать в диалог; участвовать в коллективном обсуждении проблем; интегрироваться в группу сверстников и строить продуктивное взаимодействие и сотрудничество со сверстниками и взрослыми.
Познавательные универсальные учебные действия включают: общеучебные, логические учебные действия, а также постановку и решение проблемы [1].
В настоящий период на смену науке о целенаправленном воздействии обучающего на ученика с целью передачи знаний пришла новая, личностно ориентированная концепция образования. Она ставит в центр образования личность учащегося, обеспечение комфортных, бесконфликтных условий её развития, реализацию её природных потенциалов. Теперь качество современного образования определяется не только объёмом знаний, но и особыми личностными характеристиками, делающими человека способным к диалогу с окружающей его социальной средой Многие школьники теряют интерес к изучению математики из-за трудностей в её усвоении, в силу различных способностей и имеющегося уровня знаний. Это означает, что содержание и процесс проведения внеклассных занятий должны максимально учитывать возможности и особенности каждого учащегося.
Внеклассная работа по математике формирует и развивает способности и личность ребёнка. Под внеклассной работой понимается не обязательные, систематические занятия с учащимися во внеурочное время. Математические школы, факультативные занятия и кружки призваны углублять математические знания школьников, уже определивших основной круг своих учебных интересов. Внеклассная работа представляет собой совокупность различных видов деятельности и обладает широкими возможностями воспитательного воздействия на ребенка [2]. Основываясь на выводах возрастной психологии о том, что учащиеся младшего подросткового возраста имеют низкий уровень внимательности, непоседливость, высокую общую энергию и готовность участвовать в разных видах деятельности, целесообразно вовлечение всех членов кружка в математические состязания. Образовательная и воспитательная ценность такой формы работы в том, что она активизирует мыслительную деятельность учащихся, развивает их находчивость и активность, расширяет кругозор.
В статье представлено занятие кружка по итогам второй четверти на 40 минут в виде игры-путешествия, для которого подобраны задачи по различным темам, изученным в течение двух четвертей. За три недели до этого ребятам было предложено, разбившись на группы, придумать карты путешествий для кружковых занятий в виде игры-путешествия. Три занятия в виде игры-путешествия были проведены с помощью учителя в первой четверти. Дети с энтузиазмом взялись за эту творческую работу, принесли несколько карт. Одну из них, мы и отобрали для итогового занятия, остальные реализовали постепенно до конца учебного года. Группа из 4 учеников, совместно с учителем, составляли маршруты, подбирали задачи, были ведущими на этом занятии.
Цель мероприятия: Выявить математически одаренных детей в школе, дать им возможность самовыражения и самореализации.
Задачи:
1. Создание условий для творческого самовыражения, самоутверждения учащихся.
2. Содействие формированию творчески активной, развитой личности ребёнка.
3. Развитие мотивации к дальнейшему совершенствованию знаний.
4. Повысить познавательный интерес учащихся 5классов к математике.
5. Развитие у детей логического мышления и смекалки.
Актуальность мероприятия. Знания, умения, навыки – вот три кита, на которых стояла система традиционного обучения. Действующие ранее образовательные стандарты акцентировали внимание на предметном содержании образования. Актуальной проблемой развития современного образования является введение федеральных государственных образовательных стандартов общего образования (ФГОС ОО). Формирование универсальных учебных действий (УУД) определяют как ключевой аспект новых ФГОС. В основе введения стандартов нового поколения лежит системно-деятельностный подход в образовании. Главная задача, которая стоит перед нами учителями – это научить ребенка думать, развивать его мышление. Данное мероприятие способствует развитию у детей логического мышления, математической смекалки, учит детей применять свои знания при решении практических задач.
Введение (личностные, коммуникативные и регулятивные УУД).
1-й ученик Никита. Я изобрел прибор «М-15», он поможет нам сегодня переместиться во времени на 15 лет вперед, вот и посмотрим, какие предметы нам будут там больше всего, куда нужно будет поступать учиться после школы. Ой, проводок один отвалился! Сейчас я его припаяю.
2-я ученица Наташа. А вернуться, Никита, мы сможем?
1-й ученик Никита: Не переживайте, все под контролем!
Музыкальная пауза, грохот, молния…
3-й ученик Максим: «Какая тишина вокруг, самолеты не летают, сотовый телефон не работает, машин не видно и не слышно. Никита, кажется, твой прибор забросил нас во времени на 150 лет назад!?!»
Задания внеклассного мероприятия позволяют формировать познавательные, личностные и коммуникативные УУД у учащихся.
Смотрите, скала, а рядом бродит мужчина, давайте спросим у него дорогу. «Как не помочь, да только задала мне задачку хозяйка Медной горы: из частей двух цветков сложить круг».
Мы можем вам помочь, у нас такое домашнее задание было. Помните талантливого «умельца» мастера Данилу из сказки П. Бажова «Каменный цветок»?
Задача № 1. Из частей этих двух цветков сложите круг! [2]
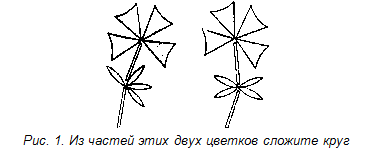
Решение.
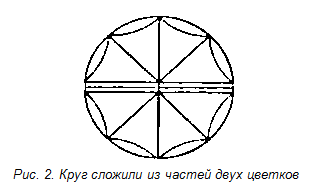
К нам приближаются вооруженные всадники с нагайками. Устроили нам допрос, кто мы и откуда прибыли. Не поверили нам и заперли в пещере.
Утром привезли таинственный документ шифровку, а часть шифра исчезла, не разгадаем, где клад зарыт, нас не отпустят.
Задача № 2.
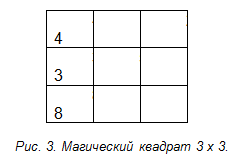
Из истории математики. Так это же волшебные или магические квадраты! Придуманы они были впервые, по-видимому, китайцами, так как самые раннее упоминание о них встречается в китайской книге, написанной за 4000-5000 лет до нашей эры. Старейший в мире волшебный квадрат китайцев представлен в виде черных кружков, которыми изображены четные (женственные) числа, белыми – нечетные (мужественные) числа.
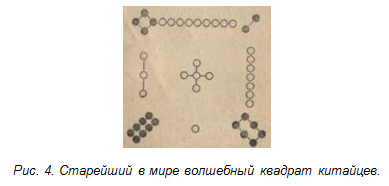
В обычной записи он не так эффектен:
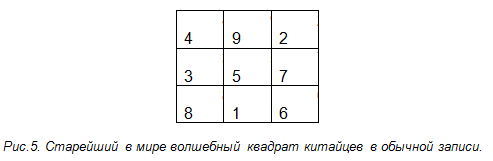
Какой это великолепный образец кросс-сумм! Девять порядковых чисел размещены в девяти клетках квадрата так, что суммы чисел вдоль каждой строки, каждого столбца и каждой из двух диагоналей одинаковы. Это и есть основное свойство волшебного квадрата [3].
Стражники были настолько поражены, что тот час отпустили нас, указав дорогу дальше.
Смотрите, строят новый дом из бревен, а у мужчин только топоры в руках, не видно строительных кранов и они так громко спорят о чем-то. Бревна зачем-то раскладывают на земле, квадраты из них складывают.
Задача № 3. Геометрия на спичках. Сколько одинаковых квадратов-срубов изб можно составить из 24 бревен, не распиливая и не ломая их, и используя при этом все бревна [4].
Решение. Если на каждую сторону квадрата сруба употребить по 6 бревен (больше нельзя), то получится один квадрат. При стороне квадрата в 5 или 4 бревна одинаковых квадратов из всех 24 бревен не получится. При стороне в 3 бревна можно выложить два квадрата. При стороне квадрата в 2 бревна - три квадрата. Обратите внимание, что из квадратов со сторонами 3 и 2 бревна можно образовать еще дополнительные квадраты других размеров, если их наложить углом друг на друга и четыре дополнительных квадрата из квадратов со стороной в два бревна. Если же из каждых четырех бревен составлять один квадрат, то из 24 бревен можно образовать 6 одинаковых квадратов.
На краю деревни около кузницы стоят лошади, а у одного коня помощник кузнеца копыта чистит и подковы снимает.
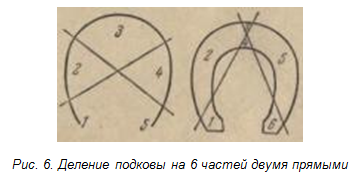
Задача № 4. Нарисуйте подкову и сообразите, как провести две прямые линии, вдоль которых можно было бы разрезать подкову на 6 частей, не перемещая их при разрезании [4].
Решение. Здесь нельзя ограничиться схематическим изображением подковы в виде дуги. Если не придать фигуре подковы необходимой объемности, то, сколько не старайтесь, вам не удастся разрезать ее вдоль двух прямых линий больше, чем на 5 частей, поэтому изобразите подкову, соответствующую действительности, постройте две пересекающие прямые на верхней части подковы, а также каждая из двух прямых должна пересечь концы подковы.
Рядом с кузницей пруд, а в нем водятся раки, давайте наловим их и пообедаем, но сначала ответим на вопросы садовника. И это мы знаем! Есть солнечные часы, а есть цветочные, я у бабушки на даче видела!
Задача № 5. Определите время по часам.

Решение (из истории математики). В старину часто пользовались солнечными часами, они известны более 3000 лет. В солнечных часах время определяется по положению тени от наклонного стержня на циферблате (циферблат и стержень располагали так, чтобы в полдень тень от стержня была направлена на отметку 12 часов). Подумайте, что общего у солнечных часов с современными часами, в чем их достоинства и недостатки [2].
Задача № 6. Спичечный рак ползет вверх. Переложить три спички так, чтобы он пополз вниз [4].

Решение. Убрать три спички с правой стороны и переложить на левую сторону рака.

Какой красивый дом-крепость, но как попасть туда, какой глубокий ров?!
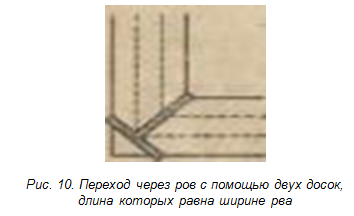
Задача № 7. Четырехугольное поле окружено рвом, ширина которого всюду одинакова. Даны две доски, длина каждой из которых равна точно ширине рва, и требуется с помощью этих досок устроить переход через ров [5].
Мы решали задачу об отряде солдат, а эта задача такая же!
Решение. Одну доску положить на угол рва, а вторую доску – одним концом на первую доску, второй конец доски – на противоположный угол рва.
Смотрите, сидит мальчик и плачет над шахматной доской, а по ней жуки ползают! Не плачь, гувернер тебе задал нетрудную задачу, мы тебе поможем и задачу решить, и жуков на клетки посадить!
Задача № 8. Представьте себе, что вам удалось поймать 25 жуков и рассадить их по одному на каждой клетке куска шахматной доски размером 5х5. Давайте предположим теперь, что каждый жук переполз на соседнюю по горизонтали или вертикали клетку этого куска доски. Как вы думаете, останутся ли при этом пустые клетки? [6]
Решение. Как бы жуки не переползали, всегда останется пустая клетка. Действительно, назовем черными тех жуков, которые сначала сидели на черных клетках, а остальных назовем белыми. После того, как каждый жук переполз на соседнюю клетку, все черные жуки оказались на белых клетках. Мы имеем 13 черных жуков и только 12 белых клеток. Значит, на некоторой белой клетке встретятся, по крайней мере, два жука. Но тогда одна клетка доски останется пустой, ведь число клеток равно числу жуков. Точно такой же ответ будет в случае любой квадратной доски с нечетным числом клеток. Подтвердить это можно по аналогичным рассуждениям.
Удивился гувернер, что мы так быстро решили эту задачу и предложил нам пройти к хозяевам дома, которые делили табун лошадей, доставшийся им по завещанию родственника.
Задача №9. Родственник распорядился, чтобы они после его смерти поделили табун лошадей между двумя племянниками и племянницей так, чтобы старший племянник взял половину всех лошадей, второй племянник – треть и племянница – девятую часть всех лошадей. В табуне 17 лошадей. Родственники начали дележ, но оказалось, что число 17 не делится, ни 2, ни на 3, ни на 9. Обратились к гувернеру, но он не смог им помочь. Помогите теперь вы [7].
Решение. Эта задача решается просто, но для начала приведите нам еще одну лошадь. Прибавим к вашим 17 лошадям еще одну лошадь, их станет 18 лошадей. Разделим это число, как и сказано в завещании, тогда старший племянник получит половину табуна, то есть 9 лошадей. Второй – треть табуна, то есть 6 лошадей, а племянница девятую часть, значит 2 лошади. Взятую 18 лошадь вернули в конюшню. Проверяем: 9 + 6 + 2 = 17 лошадей. Секрет задачи заключается в том, что части, на которые по завещанию, должны делить табун наследники, в сумме не составляет 1.
Предложили нам гостеприимные хозяева отдохнуть, заночевав у них. А утром, проснувшись, Максим обнаружил, что он у себя дома и это был просто сон.
Рефлексия (личностные, коммуникативные и регулятивные УУД).
Учитель:
- Чем вам понравилось это занятие?
- Какие задачи вспомнили быстро?
- Какая задача вызвала затруднение?
- Сделайте вывод: хватит ли нам знаний по математике, если мы окажемся на 15 лет в будущем? А почему их, по-вашему, будет недостаточно?
- Почему у Никиты произошел сбой в программе?
- Хотели бы вы провести еще такие игры – путешествие?
- Кто будет продолжать заниматься в кружке и во втором полугодии?
Домашнее задание на каникулы: Кроссворд, задача № 935. [10]
Ссылки на источники
1. Горев П. М. Основные формы организации дополнительного математического образования в средней школе // Концепт. – 2013. – № 05 (май). – ART 13116. – URL: http://ekoncept.ru/2013/13116.htm. 5. [ Дата обращения 14.05.2014]2. Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки.- Киров: АСА, 1994.- 272с.[ Дата обращения 17.04.2014]
3. Б. А. Кордемский. Математическая смекалка. Государственное издательство физико-математической литературы. М. 1958 – 10с,260с, 261с.,85, 99с. .[ Дата обращения 21.04.2014]
4. Е. И. Игнатьев. В царстве смекалки. Москва «Наука». Главная редакция физико-математической литературы. 1982 год.-11с. , .[ Дата обращения 27.04.2014]
5. Горев П. М. Уроки развивающей математики в 5–6-х классах средней школы // Концепт. – 2012. – № 10 (октябрь). – ART 12132. – URL: http://e-koncept.ru/2012/12132.htm. .[ Дата обращения 14.05.2014]
6. Горев П. М., Утёмов В. В. Двадцать хитроумных задачек Совёнка: Учебное пособие. – Киров: Издво МЦИТО, 2015. – 30 с. .[ Дата обращения 17.05.2014]
7. Горев П. М., Утёмов В. В. Уроки развивающей математики. 5–6 классы: Задачи математического кружка: Учебное пособие. Киров: Изд-во МЦИТО, 2014. – 207 с. .[ Дата обращения 17.05.2014]

