Одной из важнейших задач современной школы является интеллектуальное развитие учащихся. Нельзя не согласиться с В. А. Сухомлинским, который считал, что «невежда опасен для общества. Невежда не может быть счастлив сам и причиняет вред другим. Вышедший из стен школы может что-то и не знать, но он обязан быть умным человеком» [1].
Школа призвана внести свой вклад в подготовку личности, способной творчески решать поставленные перед ней задачи. Воспитанию такой личности способствуют инновационные педагогические технологии. На уроках математики создается проблемная ситуация, позволяющая помочь учащимся увидеть неоднозначный ответ на поставленный вопрос [2, 3].
Например, урок по теме «Определение тригонометрических функций числового аргумента».
Блок 1 – мотивация
Зная определения тригонометрических функций угла в прямоугольном треугольнике, попробуем расширить эти понятия не только для острого угла, но и для любого угла, выраженного в радианах.
Известно понятие координатной прямой. Координатная прямая задана, если на произвольной прямой выбрано начало измерения и положительное направление откладывания чисел.
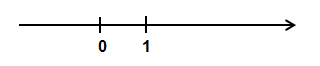Рис. 1Вопрос – существуют ли другие координатные линии, на которых можно было бы откладывать заданные числа?
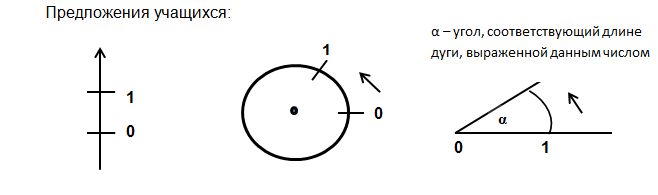Рис. 2.Учащиеся знают понятие координатной прямой: прямая, имеющая начало отсчета, единицу измерения и положительное направление отсчета чисел. Им предлагается придумать свою координатную линию, на которой можно было бы откладывать точки, соответствующие заданным числам, причем числа эти должны иметь вид:
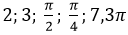и т. п.
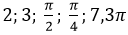и т. п.После обсуждения предложений учащихся и выбора единичной окружности как координатной линии и выбора единичного отрезка логичного переходим к следующему блоку.
Блок 2 – содержательная часть.
Учащиеся, выполняя разные варианты задания, должны отложить на единичной окружности и на прямой точки, соответствующие числам и провести сравнительный анализ построения точек на прямой и на окружности, выделить достоинства и недостатки каждого способа изображения чисел:
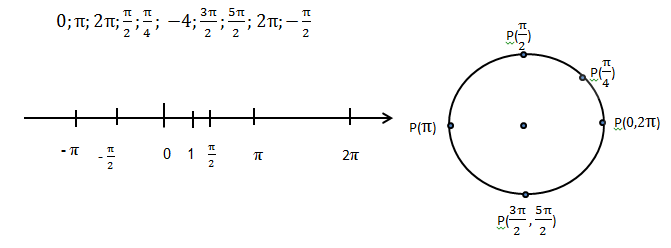
Рис. 3
Учащимся предлагается поместить единичную окружность в декартовую систему координат и выбрать наиболее удобное расположение единиц по осям координат, после чего учащиеся находят координаты точек, построенных на окружности в декартовой системе координат. Наиболее удачные комбинации предлагаются для общего обсуждения.
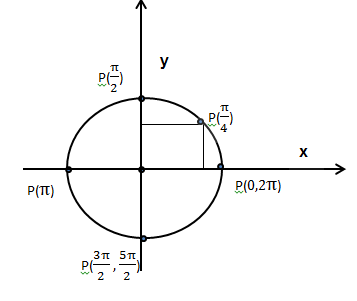Рис. 4.После обсуждения повторяем определение синуса острого угла на примере прямоугольного треугольника А. При этом учащиеся отвечают на вопрос: Как можно было бы (или это невозможно) ввести понятие синуса угла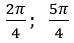
?
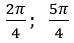?После коллективного обсуждения предложений учащихся вводятся определения всех тригонометрических функций.
Для предотвращения информационных перегрузок у учащихся переходим к блоку 3.
Блок 3 – психологическая разгрузка
После достаточно напряженной умственной деятельности можно провести тренинг для сохранения зрения учащихся: закрыть глаза, крепко зажмурить их и, не поворачивая головы посмотреть вправо, вверх, влево, вниз (3–4 раза). Изменить направление вращения глазного яблока и снова повторить упражнение.
Можно задать вопрос: на какой угол выполнено вращение?
Блок 4 – лабораторная работа
В этом блоке учащиеся выполняют лабораторную работу и отвечают на вопрос: как, используя ранее известные значения тригонометрических функций, найти значения тригонометрических функций следующих чисел:
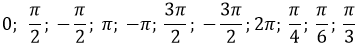
Способы нахождения этих значений предлагаются учащимися.
Наиболее популярными значениями тригонометрических функций являются значения для чисел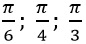 
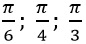
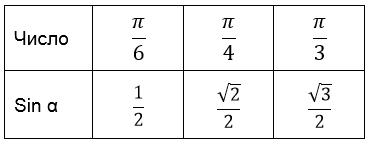
Выводим на экран таблицу
Таблица 1
Итог урока: новое определение тригонометрических функций любого числа.
На экран вывести оценку за урок.
Ссылки на источники
- Сухомлинский В. А. Избранные педагогические произведения: В 3 т., т. 2. – М. Педагогика, 1980.
- Горев П. М., Утёмов В. В. Тренинг креативного мышления: краткий курс научного творчества. –Саарбрюкен, 2012. – 84 с.
- Утемов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: прикладной курс научного творчества: учебное пособие. – Киров: Изд-во ВятГГУ, 2013. – 244 c