Задачи по формированию универсальных учебных действий на уроках математики

Предметные результаты образовательной деятельности выражаются в получении опыта приобретения, преобразования и применения предметных знаний [3].

Под метапредметными результатами понимаются универсальные учебные действия, которые становятся основой умения учиться [2].

Выделяются познавательные, коммуникативные и регулятивные универсальные учебные действия.

Познавательные УУД (их не следует путать с предметными) предполагают умение учащегося формулировать проблему, выдвигать аргументы, строить логическую цепь рассуждений, находить доказательства, подтверждающие или опровергающие тезис; осуществлять библиографический поиск, извлекать необходимую информацию из различных источников; определять основную и второстепенную информацию, осмысливать цель чтения, выбирая вид чтения в зависимости от коммуникативной цели; применять методы информационного поиска, в том числе с помощью компьютерных средств; перерабатывать, систематизировать информацию и предъявлять её разными способами.

Коммуникативные УУД – это владение всеми видами речевой деятельности, умение строить продуктивное взаимодействие со сверстниками и взрослыми; умение адекватно воспринимать устную и письменную речь; точно, правильно, логично и выразительно излагать свою точку зрения по поставленной проблеме; соблюдать в процессе коммуникации основные нормы устной и письменной речи и правила русского речевого этикета.

Регулятивные УУД представляют собой умение ставить и адекватно формулировать цель деятельности, планировать последовательность действий и при необходимости изменять её; осуществлять самоконтроль, самооценку, самокоррекцию.

Под личностными результатами понимается сформировавшаяся в образовательном процессе система ценностных отношений обучающихся – к себе, другим участникам образовательного процесса, самому образовательному процессу и его результатам.

Новые требования к результатам образовательной деятельности диктуют новые требования к уроку как основной форме организации учебного процесса. Основными методическими принципами современного урока являются:

– субъективация (ученик становится равноправным участником образовательного процесса);

– метапредметность (формируются универсальные учебные действия);

– деятельностный подход (учащиеся самостоятельно добывают знания в ходе поисковой и исследовательской деятельности);

– рефлексивность (учащиеся становятся в ситуацию, когда необходимо проанализировать свою деятельность на уроке);

– импровизационность (учитель должен быть готов к изменениям и коррекции «хода урока» в процессе его проведения) [1].

Рассмотрим конкретные примеры формирования УУД на уроке математики.

 

Примеры заданий на уроках: проблемная задача; задание, решение которого надо обосновать, основываясь только на фактах; ситуативная задача; творческое задание (например, составить задачу по таблице или по чертежу); подведение итогов урока (учащиеся должны высказать свое отношение к уроку, опираясь только на факты); дискуссия.

Проблемные ситуации практически всего курса математики строятся на затруднении в выполнении нового задания. То есть учащиеся сначала получают задание решить задачу, которую они могут решить. Затем дается задача, похожая на предыдущую, но при этом измененная так, что у детей возникают затруднения. Возникает вопрос «а почему мы не можем ее решить?». После этого возникает вопрос «а как ее решить?». Например, на уроке по теме «Раскрытие скобок» в 7 классе можно предложить следующий этап постановки учебной задачи.

Задание 1. Решить уравнения: 9 – (4 – х ) = -1;  -4 (х + 2) = 8. Учащиеся решают эти уравнения.

9 – (4 – х ) = -1,

4 – х = 9 – (-1),

4 – х = 9 + 1,

4 – х = 10,

х = 4 – 10,

х = -6.

Ответ: -6.

-4 (х + 2) = 8,

х + 2 = 8 : (-4),

х + 2 = -2,

х = -2 – 2,

х = -4.

Ответ: -4.

Решить уравнения: х – (5 – х ) = -2 и 5х – 5 (х + 3) + х = 10. Дети испытывают затруднение, так как они умеют решать уравнения только с помощью связи между компонентами действий, а в этих уравнениях больше одного неизвестного компонента действия. С помощью наводящих вопросов учителя учащиеся формулируют цели и тему урока. В конце урока необходимо вернуться к этим уравнениям и решить их, применив знания, приобретенные на уроке.

 

Примеры заданий на уроках: постановка учебной задачи, проблемная задача; формулирование цели и темы урока; решение текстовых задач (в соответствии с алгоритмом, приведенным выше); ситуативная задача; преднамеренная ошибка; задания на самоконтроль и взаимоконтроль; задание «оцени результат», «выполни прикидку»; работа с учебником; подведение итогов урока.

 

Очень полезно на уроках математики устраивать дискуссии. Можно, например, разделить класс на четыре группы. Первой и второй группе дается первая задача и решение второй задачи, третьей и четвертой группе дается решение первой задачи и вторая задача. Каждая группа независимо от других решает свою задачу. Затем первой и второй группам задается вопрос, и тот, кто из них ответит быстрее, будет выбирать, кому показывать решение первой задачи, а кому быть оппонентом. Итак, один учащийся у доски показывает полное решение задачи со всеми обоснованиями, а другой учащийся – его оппонент – внимательно слушает, а затем или оспаривает решение, или соглашается с ним, также обосновывая свои действия. Третья и четвертая группы при этом являются экспертами, которые затем высказывают свое мнение о ходе дискуссии, опираясь на готовое решение задачи. После этого группы меняются ролями и приступают к обсуждению решения второй задачи. Одновременно можно рассмотреть и другие способы решения данных задач.

Задания на самопроверку и взаимопроверку. Рассмотрим организацию работы на примере проведения математического диктанта.

 

Примеры заданий на уроках: работа с учебником, проблемная задача, решение текстовых задач (в соответствии с алгоритмом, приведенным выше), ситуативная задача, задачи с избытком информации (требуется отделить значимую информацию от второстепенной), задачи с недостатком информации (требуется определить, какой информации недостает и где ее найти), использование знаково-символьных средств при обработке информации, задание на составление математической модели, задание на формирование умения поиска ответа «угадай, о чем спросили», задание на выдвижение гипотезы, задание на доказательство какого-либо суждения.

 

1 группа работает за компьютерами.

Дается графики квадратичной функции и обратной пропорциональности. Задание: определить коэффициенты преобразования.

2 группа работает устно: Задайте функции параболы и гиперболы, изображенных на рисунке 1 (у детей заранее заготовленные формулы, задающие данные функции, из которых они выбирают нужную):

 

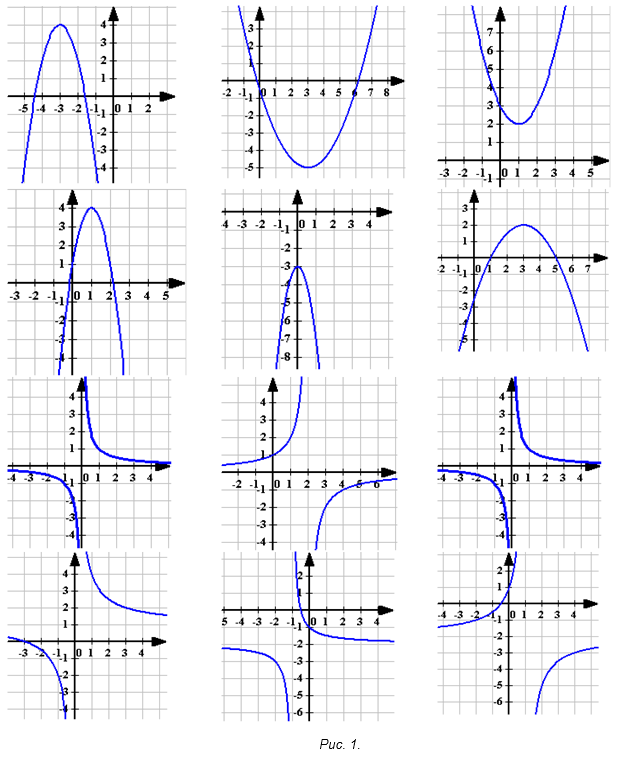
Итак, какие преобразования графиков вы знаете? Каким образом это отражено в формуле функции, которая задает этот график?

Все последние уроки мы с вами посвятили обыкновенным дробям с разными знаменателями. Складывали, вычитали, сравнивали их. Единственное, о чем мы не говорили, – это их происхождение.

Так вот, чтобы не попасть в трудное положение сегодня на уроке, давайте вспомним порядок действий с двумя обыкновенными дробями с разными знаменателями.

Учащиеся вспоминают и проговаривают вслух правило.

Дома вы должны были написать правило в стихах. Посмотрим, как это у вас получилось. А жюри оценит все шедевры.

            /1/

            Если дроби нужно нам сложить,

            Общим знаменатель должен быть,

            И на дополнительные множители

            Числители слагаемых умножим мы.

            /2/

            Нам учитель дал заданье

            Сумму двух дробей узнать.

            Чтобы сделать то заданье,

            Надо следующее знать:

            Знаменатель нужно общий нам для этого найти,

            Множитель к дробям приставить,

            Чтоб значенье не менять,

            Два числителя мы сложим –

            Вот и все, что нужно знать.

            /3/

            Для того, чтобы дроби сложить,

            Нужно наименьший общий знаменатель определить.

            Теперь дополнительные множители найди:

            Общий знаменатель на обычный раздели,

            Дополнительный множитель над числителем подпиши.

            Дополнительные множители на числитель умножь,

            И тогда числитель ты найдешь.

            Числители сложи, а знаменатель тот же напиши.

 

Высшая точка знания правила – умение его применять. Проверим, умеем ли мы это делать.

1)  Решите уравнения (работа проводится с использованием компьютера):

х +  =

а -  =

 - у =

 + m = 0,6

2)  Решите задачи (на доске).

а) С двух сторон навстречу друг другу идут два пешехода. Расстояние между ними равно 1. Один прошел  пути, а второй . Встретились ли пешеходы?

б) В первый день мы прочитали первый рассказ, который занимает  книги, во второй день –  всей книги, а в третий – остальное. Сколько прочитали в третий день?

в) Пакет выдерживает 4 кг. Мы купили крупу – 1 кг, сыр –  кг, колбасу –  кг, конфеты – 1,5 кг, печенье –  кг, мясо – 0,8 кг. Выдержит ли пакет?

Вот, наконец, мы и подошли к самому сложному заданию. Жюри просит класс разделиться. Одна часть – к компьютерам выполнять тест, а для другой я приготовила задачу:

 

            Есть кадамба цветок;

            на один лепесток

            пчелок пятая часть опустилась.

 

            Рядом тут же росла

            вся в цвету симендга,

            и на ней третья часть поместилась.

 

            Разность их ты найди,

            трижды их ты сложи,

            на кутай этих пчел посади.

 

            Лишь одна не нашла

            себе места нигде,

            все летала то взад, то вперед и везде

            ароматом цветов наслаждалась.

 

            Назови теперь мне,

            посчитавши в уме,

            сколько пчелок всего здесь собралось?

 

                              (Бхаскара, индусский математик ХII в.)

 

Примеры заданий на уроках: работа в парах или группах, задать вопрос по учебному материалу и ответить на него, дискуссия, обоснование этапов решения задачи (или этапов доказательства суждения), прочитать суждение, записанное с помощью символов, и, наоборот, записать с помощью символов какое-нибудь суждение.

 

Преобразования графика

Дискуссия иобоснование этапов решения по определению вида преобразования графика до построения.

Пользуясь тремя типами преобразований графиков – параллельным переносом, растяжением (сжатием) и симметрией, можно исходя из графика функции у=f(x) построить график функции y=аf(x+b)+c при любых значениях параметров a, b, c. (графики демонстрируются в специальной программной среде)

Графики функций  и . (симметрия относительно оси Ох)

Графики функций у=х² и у=3х² (сжатие по оси Х)

Графики функции  и  (растяжение по оси Х)

Графики функции у=х² и у = (х-5)² (параллельный перенос параболы на 5 единиц вдоль оси Ох вправо)

Графики функции у=х² и у = (х+5)² (параллельный перенос параболы на 5 единиц вдоль оси Ох влево)

Сделаем вывод: как построить график функции у=f(x+b), если известен график функции у=f(х) (посредством переноса на b единиц влево, если b>0, и вправо, если b<0).

Графики функции у=2х² и у=2х²+3 (параллельный перенос параболы на 3 единицы вверх по оси Оу)

Графики функции у= и  (параллельный перенос на 4 единицы масштаба вниз вдоль оси у)

Сделаем вывод: как построить график функции у=f(х)+c, если известен график функции у=f(х) (посредством переноса на с единиц вверх, если c>0, и вниз, если c<0).

Графики функции у=2,5х² и у=2,5(х+3)²+4 (параллельный перенос на 3 единицы влево и на 4 единицы масштаба вверх)

Сделаем вывод: как построить график функции у=аf(х+b)+c, если известен график функции у=аf(х) (посредством переноса на b единиц влево, если b>0, и вправо, если b<0, посредством переноса на с единиц вверх, если c>0, и вниз, если c<0).

Вот и подошел, наконец, долгожданный день, когда мы участвуем в конкурсной программе. Хотелось бы представить жюри: официальное – гости, присутствующие на уроке, и неофициальное – компьютер. И цель урока – понравиться жюри и заслужить его высокие оценки.

Прежде чем участвовать в серьезных соревнованиях, мы должны размяться и привести наши мысли в порядок. Разминку подготовил и будет судить компьютер.

Устный счет.

На экране – мордочка. Если учащиеся угадывают цифру или знак верно, то мордочка смеется, иначе – плачет.

а) Восстановите цифры и знаки действий:

 

3 . 5, 6 7 .                .  .  . .

2 0 ., .  . 9                      . 2 

   96,8 8 9             1 8 . 4 8

                           74 9 9 .

                            . . .  6 6 .

Наш компьютер больше улыбался, чем грустил, значит, мы ему понравились. Закрепим успех.

 

б) Сократите дроби:

в) Превратите в неправильную дробь:

г) Выделите целую и дробную части: