- Определенный фонд знаний и умений, их качество и степень обобщенности.
- Уровень развития: внимания, памяти, воображения.
- Уровень развития мышления, который определяется степенью сложности умственных действий и операций (анализ, синтез, сравнение, обобщение, классификация, конкретизация).
- Владение приемами поисковой и творческой деятельности.
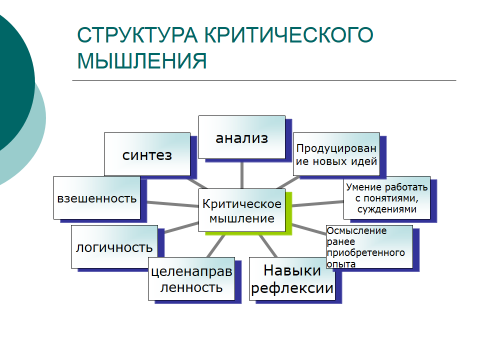
- Критическое мышление есть мышление самостоятельное.
- Информация является отправным, а отнюдь не конечным пунктом критического мышления.
- Критическое мышление начинается с постановки вопросов и уяснения проблем, которые нужно решить.
- Критическое мышление стремится к убедительной аргументации.
- Критическое мышление есть мышление социальное.
|
I фаза Вызов |
II фаза Осмысление содержания |
III фаза Рефлексия |
|
пробуждение имеющихся знаний, интереса к получению новой информации |
Получение новой информации |
осмысление, рождение нового знания |
|
№ |
Приём |
Содержание |
||||||||
|
1 |
Кластер |
Графический прием в систематизации материала. Он может быть использован на всех стадиях урока, в том числе и на стадии осмысления |
||||||||
|
2 |
«П»–«М»–«И»: таблица «Плюс–минус–интересно» |
Заполнение таблицы помогает организовать работу с информацией на стадии осмысления. Новая информация заносится в таблицу; по ходу чтения параграфа или прослушивания лекции заполняются соответствующие графы. Прием нацелен на актуализацию эмоциональных отношений в связи с текстом. При использовании этого приема информация не только более активно воспринимается (прослушивается, записывается), систематизируется, но и оценивается. Подобная форма организации материала позволяет провести обсуждение, дискуссию по спорным вопросам. |
||||||||
|
3 |
«Кубик» |
Суть данного приема. Из плотной бумаги склеивается кубик. На каждой стороне пишется одно из следующих заданий: 1 Опиши это... (Опиши цвет, форму, размеры или другие характеристики). 2 Сравни это... (На что это похоже? Чем отличается?) 3 Проассоциируй это... (Что это напоминает?) 4 Проанализируй это... (Как это сделано? Из чего состоит?) 5 Примени это... (Что с этим можно делать? Как это применяется?) 6 Приведи «за» и «против» (Поддержи или опровергни это). Ученики делятся на группы. Учитель бросает кубик над каждым столом и таким образом определяется, в каком ракурсе будет группа осмыслять ту или иную тему занятия. Учащиеся могут писать письменные эссе на свою тему, могут выступить с групповым сообщением и т.п. Этот приём: - создает на уроке целостное (многогранное) представление об изучаемом материале; - создает условия для конструктивной интерпретации полученной информации. |
||||||||
|
4 |
«Сводная таблица» или сравнительная таблица |
Такие таблицы помогают учащимся увидеть не только отличительные признаки объектов, но и позволяют быстрее и прочнее запоминать информацию. Составление сравнительных таблиц можно использовать как на стадии вызова, так и на стадии осмысления. Проделанная работа развивает у ребят следующие умения: - выделять ключевые слова; - систематизировать необходимую информацию; - анализировать, сравнивать и обобщать информацию; - развивать монологическую речь. |
||||||||
|
5 |
Таблица «Толстых» и «Тонких» вопросов
|
Способ активной фиксации вопросов по ходу чтения, слушания; при размышлении – демонстрация пройденного.
|
||||||||
|
6 |
Таблица «ИНСЕРТ» |
I – interactive N – noting - самоактивизирующая «V» – уже знал S – system - системная разметка «+» – новое Е – effective для эффективного «-» - думал иначе R – readingand – чтения и Т – thinking - размышления – «?» не понял, есть вопросы. Таблица «Инсерт», имеет вид:
Для заполнения таблицы ученикам понадобится вновь вернуться к тексту. Таким образом, обеспечивается вдумчивое, внимательное чтение. Этот прием делает зримым процесс накопления информации, путь от «старого» знания к «новому» – понятным и четким. |
технологии критического мышления
|
Этапы урока |
Деятельность учителя |
Деятельность учащихся |
|||||||||||||||||||||||
|
Стадия вызова |
|||||||||||||||||||||||||
|
1. Орг. Момент (1–2 мин.) |
Я рада вас всех видеть. Чтобы начать работу, проверим, всё ли готово к уроку. |
Класс готовится для работы, включаются в деловой ритм. |
|||||||||||||||||||||||
|
2. Целеполагание и мотивация (3–5 мин.) |
Математика – наука древняя, интересная и полезная. Сегодня мы с вами в очередной раз убедимся в этом, и очень хочется, чтобы каждый из вас для себя сделал хотя бы небольшое, но открытие. А как сказал великий ученый, математик Лейбниц: «Кто хочет ограничиться настоящим, без знания прошлого, тот его никогда не поймёт…», то и нам с вами для успешной работы нужно повторить некоторые геометрические фигуры и понятия, вспомнить правила для округления десятичных дробей до различных разрядов, выполнения умножения и деления десятичных дробей и нахождения неизвестных компонентов в делении и умножении.
Название нашей темы урока состоит из двух слов. Отгадайте загадку и вы узнаете одно слово темы. Если видишь солнце в небе, или чашку с молоком, Видишь бублик или обруч, слышишь сказку с колобком, В круглом зеркале увидел ты сейчас свою наружность. И вдруг понял, что фигура называется окружность. А другое слово вы узнаете, выполнив следующее задание. Найдите отношение чисел 22/7, 2/7 и полученный результат округлите до десятичных. Так какая тема сегодняшнего урока? Правильно, – «Длина окружности». Откройте тетради, запишите число и тему урока: «Длина окружности» Игра «верю и не верю»
Давайте, сформулируем цель нашего урока. |
Открывают тетради и записывают тему в тетрадь.
Заполняют таблицу индивидуально.
Выбирают или придумывают цель, записывают в тетрадь.
|
|||||||||||||||||||||||
|
Стадия осмысления |
|||||||||||||||||||||||||
|
3. Актуализация (10 мин.) |
Предлагаю вам текст. Задание 1. Познакомьтесь с информацией. Самая простая из кривых линий – окружность. Это одна из древнейших геометрических фигур. Ещё вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает «луч». В Древней Греции круг и окружность считались венцом совершенства. В русском языке слово «круглый» тоже стало означать высокую степень чего-либо: «круглый отличник», «круглый сирота» и даже «круглый дурак». Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас. Окружности и циклы идут, взявшись за руки. Циклы получаются при движении по кругу. Мы изучаем циклы земли, они помогают нам разобраться, когда надо сажать растения и когда мы должны вставать. Представление об окружности даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса, спицы которого соответствуют радиусам окружности. Термин «хорда» (от греческого «струна») был введён в современном смысле европейскими учёными в XII-XIII веках. По материалам книг: Г. Глейзер «История математики в школе», С. Акимова «Занимательная математика».
Задание 2. Заполните таблицу «Инсерт».
Задание 3. Изучив таблицу, сформулируйте геометрические определения понятий, используя ключевые слова.
|
Парами работают с информацией.
Заполнение таблицы. Работа индивидуально.
Заполняют таблицу индивидуально, затем работа в парах и озвучивают информацию.
|
|||||||||||||||||||||||
|
4. Физ. Минутка (2 мин.) |
Ребята, давайте перед практической работой сделаем разминку. Сядьте ровно. Покажите мне руками маленькую окружность. А теперь представьте, что наша окружность раздувается, становится все больше и больше. Показываем, вот какая получилась окружность. А теперь поднимаем эту окружность над собой и держим над головой. Представим, что подул ветер и наша окружность наклоняется сначала влево, потом вправо. А теперь представим, что окружность превратилась в воздушный шарик и отпускаем ее. Молодцы! Приступаем к работе! |
Фронтальная работа
Выполняют разминку. |
|||||||||||||||||||||||
|
5. Практическая работа №1 (10 мин.) |
Создание проблемной ситуации. Можно ли измерить длину окружности? С помощью какого измерительного прибора это можно сделать? Как это можно сделать? В далёкой древности было установлено, что также есть зависимость между длиной окружности и её диаметром. Давайте же и мы попробуем её установить, для этого вы выполните практическую работу, в которой будете использовать способ измерения длины окружности, предложенный вами, но для удобства будете пользоваться ниткой. У вас на столах находятся различные предметы: - стакан; - трёхлитровая банка; - компакт-диск. - блюдце. Работать вы будете по парам. Приготовили циркули, линейки и карандаши, нитки. Этап: Практическая работа №1. Самостоятельная работа учащихся (Заполнение таблицы).
Если бы мы, ребята, еще более точно измерили длину окружности, ее диаметр и более точно выполнили вычисления длины окружности к ее диаметру, то получили бы число 3,14… Это число математики обозначают буквой (пи). |
Учащиеся выполняют практические задания по команде учителя и записывают свои наблюдения.
Заполняют сравнительную таблицу. (приводится внизу)
Учащиеся делают вывод:
Далее ученики называют свои результаты и замечают, что, хотя окружности были у всех разные, отношения длины к диаметру получились примерно одинаковые – отношения больше 3, но меньше 4. Значит, можно записать: 3< <4 Происходит первичное осознание полученных результатов, а именно: отношение длины окружности к ее диаметру есть число постоянное. Первое знакомство с числом Пи. |
|||||||||||||||||||||||
|
6. Историческая справка (3 мин.) |
Число π – бесконечная десятичная дробь. Обозначение числа происходит от первой буквы греческого слова периферия, что означает «окружность». Общепринятым это обозначение стало, после издания одной из работ Эйлера. На ранних ступенях человеческого развития пользовались неточным числом π. Оно было равно 3. Египетские и римские математики установили отношение длины окружности к диаметру не строгим геометрическим расчётом, как позднейшие математики, а нашли его просто из опыта. В III в. до н.э. Архимед без измерений, одними рассуждениями, вычислил точное значение числа = 22/7. Двадцать две совы скучали На больших сухих суках. Двадцать две совы мечтали О семи больших мышах, О мышах довольно юрких В аккуратных серых шкурках. Слюнки капали с усов У огромных серых сов
|
Просматривают, прослушивают и запоминают |
|||||||||||||||||||||||
|
7. Практическая работа №2 (5 мин.) |
Вывод формулы длины окружности. Итак, мы имеем следующее соотношение:
Выведем из этой формулы С= d или С=2 R. Эта формула называется формулой длины окружности. Чтобы найти длину окружности, надо знать её радиус или диаметр. Задание. Вычислить по формуле длину своей окружности. Сравнить результаты, полученные опытным путем и с помощью применения формул. |
Индивидуальная работа
Сравнивают результаты, полученные опытным путем и с помощью применения формул, делают выводы. |
|||||||||||||||||||||||
|
8. Информирование о д/з (1 мин.) |
На дом учащимся предлагаются задания по выбору уровня сложности (3 уровня). |
Учащиеся самостоятельно выбирают себе уровень и по желанию можно сделать не только тот уровень, который выбрали, но и уровень выше. |
|||||||||||||||||||||||
|
Стадия рефлексии |
|||||||||||||||||||||||||
|
9. Подведение итогов. Рефлексия (5 мин.) |
Подведение итогов. Рефлексия. Ответьте на вопросы Достигли ли вы своей цели на уроке? Что делали? Зачем делали? Как делали? Для чего делали?
|
Отвечают на вопросы, поставленные на уроке. Учащиеся заполняют свои оценочные карты. Некоторым можно дать возможность высказать свое мнение, ассоциации, мысли. Сегодня я узнал… Было интересно… Я понял, что… Теперь я могу… Я научился… У меня получилось… Я попробую…. Меня удивило… Мне захотелось… |
|||||||||||||||||||||||