Одним из важных направлений модернизации отечественного образования является преодоление репродуктивного стиля обучения и переход к такой образовательной системе, которая бы в полной мере могла обеспечить познавательную активность и самостоятельность мышления учащихся. Федеральный государственный образовательный стандарт основного общего образования ориентирует школу на овладение учащимися не только предметными, но и метапредметными, личностными результатами, в том числе обеспечивающими роста творческого потенциала учеников, их готовности к применению универсальных учебных действий в жизненных ситуациях [1].
Современному человеку для успешной самореализации необходимы три основных компонента: креативность, овладение информационными технологиями и коммуникативными навыками.
Креативность – это умение находить новые оригинальные идеи, которые отличаются от принятых схем мышления, успешно справляться с решением различных задач нестандартным образом. Это умение видеть проблемы под иным углом и умение решать их уникальным способом.
Перед нами, педагогами остаются проблемные вопросы: «Как сделать так, чтобы ученье проходило с увлечением?», «Как дать возможность каждому школьнику развивать свои творческие способности?», «Как удержать внимание и интерес школьника к изучению материала на протяжении всего урока?» и т.д., на которые хочется найти наиболее продуктивные ответы.
Найти ответы на эти вопросы нам поможет целостная педагогическая система НФТМ-ТРИЗ.
Креативная педагогическая система НФТМ-ТРИЗ, разработанная кировскими специалистами, призвана обучить педагога технологиям, способствующим развитию творческих способностей учащихся.
- Что же такое НФТМ-ТРИЗ?
НФТМ – непрерывное формирование творческого мышления и развитие творческих способностей учащихся.
ТРИЗ – теория решения изобретательских задач.
Цель данной системы НФТМ-ТРИЗ: формирование творческой личности учащихся.
А творческая личность – это личность, обладающая системным мышлением, способная решать творческие задачи любого уровня творчества.
- На чём основана система НФТМ-ТРИЗ?
На поисково-познавательной деятельности учащихся.
- На что направлена система НФТМ-ТРИЗ?
На развитие фантазии и творчества воображения и управление ими [2].
Использование на уроках технологии ТРИЗ, позволяет учителю создавать для школьников интересные задания. Выполняя эти задания, ученик вынужден творить, общаться с одноклассниками, создавать, фантазировать, раскрывать свои способности. Ученик не просто повторяет за учителем предложенные варианты, а сам добивается результатов, сам находит пути решения проблем. Чтобы добиться успешного результата учитель продумывает задания на каждом этапе урока.
В данной статье представлена разработка креативного урока геометрии по теме «Остроугольный, прямоугольный и тупоугольный треугольники» на основе педагогическй системы НФТМ – ТРИЗ М. М. Зиновкиной.
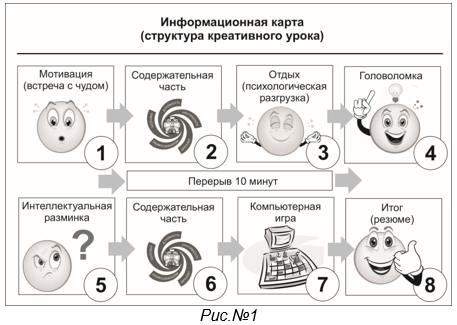
Структура креативного урока по схеме целостной системы многоуровневого непрерывного креативного образования НФТМ-ТРИЗ М. М. Зиновкиной отличается от традиционного урока и включает в себя следующие блоки, реализующие цели занятия, адекватные целям креативного образования в целом:
Блок 1 (мотивация)– (5 мин). Этот блок представляет собой специально отобранную систему оригинальных объектов – сюрпризов, способных вызвать удивление учащегося. Этот блок обеспечивает мотивацию учащегося к занятиям и развивает его любознательность.
Блоки 2 и 6 (содержательная часть) – (20 мин,15 мин). Блоки содержат программный материал учебного курса и обеспечивают формирование системного мышления и развитие творческих способностей.
Блок 3 (психологическая разгрузка) – (5мин). Блок представляет собой систему психологической разгрузки. Психологическая разгрузка реализуется через упражнения по гармонизации развития полушарий головного мозга, через аутотренинг, через систему спортивно-эмоциональных игр, театрализацию и др.
Блок 4 (головоломка) – (10 мин). Данный блок представляет собой систему усложняющихся головоломок, воплощенных в реальные объекты, в конструкции которых реализована оригинальная, остроумная идея.
Блок 5 (интеллектуальная разминка) – (10 мин). Блок представляет систему усложняющихся заданий, направленных на развитие мотивации, дивергентного и логического мышления и творческих способностей учащихся.
Блок 7 (компьютерная интеллектуальная поддержка) – (10 мин). Этот блок обеспечивает мотивацию и развитие мышления, предусматривает систему усложняющихся компьютерных игр-головоломок, адаптированных к возрасту учащихся, обеспечивает переход из внешнего плана действий во внутренний план.
Блок 8 (резюме) – (5 мин). Блок обеспечивает обратную связь с учащимися на уроке и предусматривает качественную и эмоциональную оценку учащимися самого урока [3].
Каждый креативный урок представляется информационной картой (смотри рис.№1). Информационная карта креативного урока представлена восемью блоками, указанными выше [4].
Разработка креативного урока по теме
«Остроугольный, прямоугольный и тупоугольный треугольники»
Блок 1.Мотивация
Учитель: На уроках геометрии мы часто сталкиваемся с такой проблемой: рассматривая свойства геометрических фигур, некоторые ученики иногда опираются лишь на чертеж, на свое зрительное восприятие. Но такой подход к решению задачи часто приводит к ошибочным выводам, а значит к неверному решению. Мы привыкли доверять собственному зрению, однако оно нередко обманывает нас, показывая то, чего в действительности не существует. В такие моменты мы сталкиваемся со зрительными иллюзиями – ошибками зрительного восприятия. Ученые и художники создали немало обманчивых картинок, наглядно демонстрирующих, сколь ограничены возможности человеческого глаза [5].
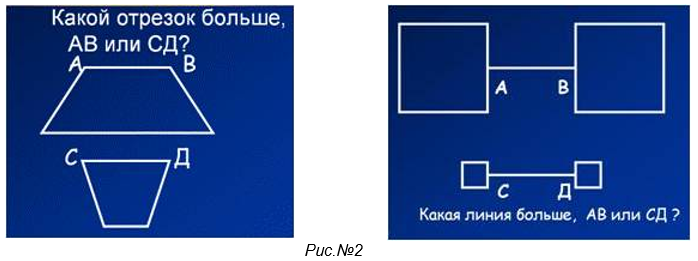
1. Рассмотрим иллюзию Болдуина (смотри рис.№2):
1. Рассмотрим иллюзию Болдуина (смотри рис.№2):
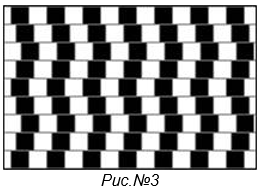
2. Иллюзия кафе (смотри рис.№3). Вопрос: Параллельны ли линии на данном рисунке?
 3. Иллюзия Эббингауза (смотри рис .№4). Вопрос: Какой круг больше? Тот, который окружен маленькими кругами или же тот, который окружен большими?
3. Иллюзия Эббингауза (смотри рис .№4). Вопрос: Какой круг больше? Тот, который окружен маленькими кругами или же тот, который окружен большими?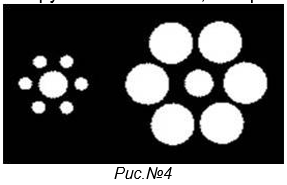 5. Иллюзия Мюллера-Лайера (смотри рис.№5). Вопрос: Какой из отрезков длиннее? Синий или красный?
5. Иллюзия Мюллера-Лайера (смотри рис.№5). Вопрос: Какой из отрезков длиннее? Синий или красный? 6. Параллелограмм Зандера (смотри рис.№6). Вопрос: Какой отрезок длиннее AB или BC?
6. Параллелограмм Зандера (смотри рис.№6). Вопрос: Какой отрезок длиннее AB или BC?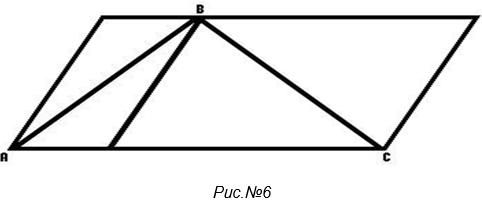
Учащиеся отвечают на вопросы, исследуют картинки, производя измерения, высказывают свои мнения, почему они видят не то, что изображено в действительности на картинке. После чего учащиеся должны сделать вывод, что в геометрии при решении задач нельзя опираться только на чертеж, надо все свои высказывания подтверждать свойствами, аксиомами, теоремами, доказывать.
Блок 2.Содержательная часть
Повторение.
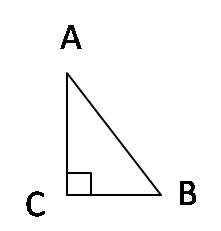
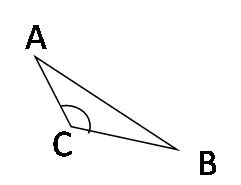
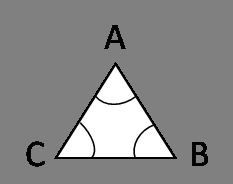
Для актуализации опорных знаний нужно вспомнить виды углов,их градусные меры и теорему о сумме углов треугольника.
Учитель просит учеников заполнить таблицу №1, тем самым учащиеся повторяют виды углов и дают определения этих углов.
Таблица 1
|
Рисунок |
Типы углов |
Свойства углов |
 |
|
|
|
|
|
Меньше |
|
|
Развернутый |
|
|
|
|
Больше, но меньше |
Проведя анализ заполнения таблицы №1, переходим к следующему заданию. Выполняяданное задание, учащиеся повторяют тем самым теорему о сумме углов треугольника, свойства углов равнобедренного, равностороннего треугольников и применяют это при решении задания.
Задание:В каждом из треугольников, изображенных на рисунке 7, найдите градусную меру неизвестных углов. (Задание для устного решения, с последующим анализом решения)

Изучение нового материала.
Проведя анализ решения задач с треугольниками переходим к изучению новой темы. Учитель предлагает учащимся заполнить пропуски в карточке №1.Сначала учащиеся заполняют пропуски во второй колонке, во всех трех случаях. Рассматривая треуольники с различными углами, учащиеся выясняют, опираясь на теорему о сумме углов треугольника, что прямой и тупой углы в треугольнике могут быть только по одному,а остальные углы острые. После чего вводятся определения (с помощью наводящих вопросов учителя) остроугольного, тупоугольного, прямоугольного треугольников, понятия гипотенузы и катета прямоугольного треугольника. Далее заполнняется третья колонка во всех трех случаях.
|
|
– … (указать тип углов)
|
…
…
…
|
|
|
… (указать тип углов)
|
… |
|
|
– … (указать тип углов)
|
…
|
Карточка №1
После ознакомления учащихся с новой темой, учитель предлагает проверить новые знания на практике.
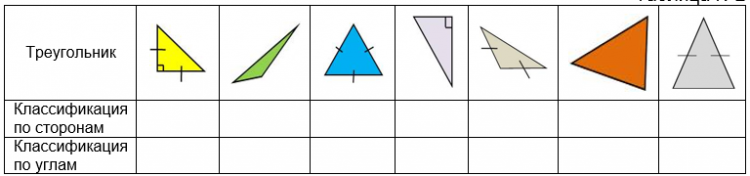
Задание: Нужно провести классификацию данных треугольников по сторонам и углам. (Учащиеся заполняют таблицу №2.)
Таблица №2
Блок 3. Психологическая разгрузка
Учитель: «Полет – это математика» – писал советский летчик Валерий Чкалов.
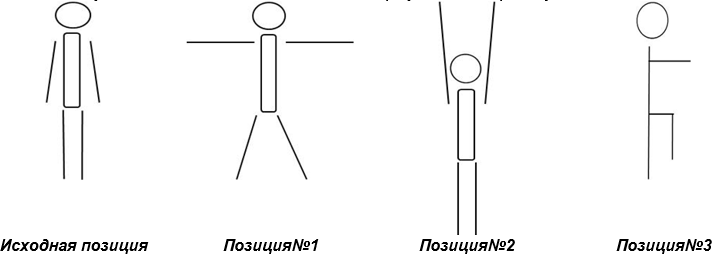
Давайте проверим, умеет ли ваша мысль летать, а заодно проверим ваше внимание. Мы будем сейчас выполнять с вами зарядку, но не простою, а математическую, которая будет связана непосредственно с нашей темой урока. Я вам буду показывать картинку, на которой будет изображен треугольник, вы должны будете определить к какому типу относится данный треугольник и показывать свои ответы с помощью соответствующих позиций (смотри рис. № 8)
Исходная позиция:Учащиеся стоят, ноги вместе, руки опущены вниз.
Следующая позиция учащихся будет зависеть от того, какой треугольник им будет продемонстрирован учителем. Если ученик считаете, что учитель демонстрирует треугольник тупоугольный, то он занимает позицию №1: ноги ставят на ширине плеч, руки в стороны. Если же остроугольный, то позицию №2: ученик встает на цыпочки и тянется руками к солнцу. Позиция №4: ногу поднять вперед, согнув при этом в коленке, при этом руки вытянуть вперед. Эта позиция занимается учеником, если он считает, что треугольник прямоугольный.
Блок 4. Головоломки.
Особенно важны аспекты работы с головоломками – своеобразный тренинг учащегося по преодолению инерции мышления [6], развитию смекалки и создания всплеска положительных эмоций (восторга) в результате её решения, появление уверенности в своих творческих возможностях. Головоломки представляют для школьника проблему, решение которой требует от него нетрадиционного поворота мысли.
Задача-смекалка:Имеется пруд в видеформыравностороннего треугольника. По углам пруда близ воды растут три старых дуба.
Пруд понадобилось увеличить, сохранив, однако, форму равностороннего треугольника. Но старых дубов трогать не желают. Можно ли увеличить площадь пруда, сохранив, однако, форму равностороннего треугольника? И причем так увеличить, чтобы 3 дуба, оставались на своих местах, не были затоплены водой, а стояли у берегов нового пруда? (смотри рис. № 9)
Ответ: Смотри рис.№ 10

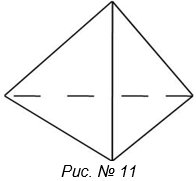
Задача со спичками: Из 6 спичек составьте 4 равных равносторонних треугольника.
Можно смело поручиться, что мало кому сразу придет в голову решение этой простой с виду задачи. Дело в том, что в данном случае приходится строить из спичек не плоскую фигуру, а фигуру в пространстве. (смотри рис. № 11)
Итак, перед учащимися была проблема, они инстинктивно, по пути, который мы трактуем как инерцию мышления, пытались разместить спички так, как они не должны были располагаться. Оказалось трудно. Но если проанализировать проблему и найти параметры в ней (здесь – это построение в пространстве, а не на плоскости), то область поиска решения сузится.
Блок 5. Интеллектуальная разминка
Предлагаю решить следующую задачу: Даны объекты (понятия) необходимо данные объекты включить в группы именно в те к которым они соответствуют.
Объекты: 1. Острый угол, 2. Равнобедренный треугольник, 3. Гипотенуза, 4. Прямой угол, 5. Разносторонний треугольник, 6. Катет, 7. Тупой угол, 8. Развернутый угол, 9. Равносторонний треугольник.
Группы:
1) Остроугольный треугольник.
2) Прямоугольный треугольник.
3) Тупоугольный треугольник.
Правильное решение:
1-я группа: 1, 2, 5, 9;
2-я группа: 1, 2, 3, 4, 5, 6
3-я группа: 1, 2, 5, 7.
Данное задание направлено на нахождение закономерностей, задания такого типа направлены на развитие логики мышления и на способность к обобщению, на выделение основных качеств и свойств объекта.
Главная функция интеллектуальной разминки состоит в подготовке к выполнению сложных заданий через осознание значимости правильно проведенного анализа информации.
Блок 6.Содержательная часть
Вернемся к содержательной части нашего урока. Следующее задание, заключается в том, что учащиеся, не видя изображение треугольника, должны найти недостающие данные (градусные меры углов треугольника и определить его вид). Учащиеся работают с карточкой №2
Проводя анализ (фронтально) решений задач из этого задания мы, скорее столкнемся с тем, что ответы учащихся в задаче №4 будут различны. Рассматривая варианты решений, учащиеся приходят к выводу, что задача имеет два решения и оба эти решения верны. Мы столкнулись с задачей частично открытого типа, в условии которой недостаточно информации.
Вопрос учителя к классу: Какой информации не хватает в условии задачи, чтобы она имела единственное решение?
- Правильный ответ: В условии задачи должно быть сказано, какой угол равнобедренного треугольника дан (либо при вершине, либо при основании).
Вопрос учителя к классу: Каким должен быть данный угол ( С) в задачи при том же условии (треугольник равнобедренный), чтобы она имела единственное решение?
Правильный ответ: Угол должен быть либо прямой, либо тупой.
|
№ |
А |
В |
С |
Вид треугольника |
|
|
По сторонам |
По углам |
||||
|
1. |
60° |
60° |
|
|
|
|
2. |
30° |
|
Прямоугольный |
||
|
3. |
35° |
110° |
|
|
|
|
4. |
70° |
Равнобедренный |
|
||
|
5. |
100° |
30° |
|
|
|
|
6. |
75° |
55° |
|
|
|
|
7. |
90° |
45° |
|
|
|
Карточка №2
В этом блоке можно рассмотреть еще такую задачу: Известно, что треугольники АВС и АDC прямоугольные и равнобедренные.
Вопрос: Следует ли из этого, что АС = АD?
В этом случае ответ может быть и утвердительным, и отрицательным в зависимости от расположения треугольников относительно друг друга. Данная задача относится к задачам открытого типа. Задачи такого рода могут быть эффективно использованы на различных этапах урока математики. Задачи открытого типа позволяют ученикам конструировать собственные знания о реальных объектах познания [7].
В данном блоке мы рассмотрели задачи с недостающими данными. В задачах такого типа отсутствуют некоторые данные вследствие чего дать точный ответ на вопрос задачи не представляется возможным. Однако, ученик должен проанализировать задачу и доказать, почему нельзя дать точного ответа на вопрос задачи, чего не хватает, что надо добавить.
Блок 7. Компьютерная интеллектуальная поддержка
С помощью компьютерной программы, пользуясь алгоритмом, дети выполняют задание
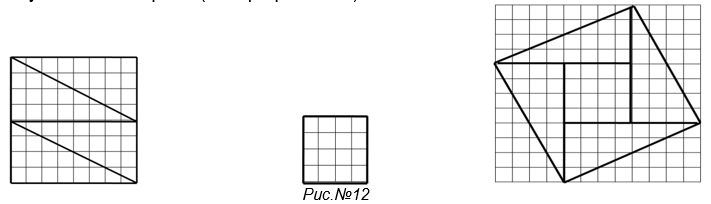
Алгоритм:
- Откройте файл на рабочем столе под именем «Сложи квадрат»
- Изобрази на клетчатом поле два квадрата: Малый квадрат (8х8) и большой квадрат(4х4).
- Раздели большой квадрат (8х8) пополам, затем каждую половину раздели на два треугольника (квадрат получился разбитый на 4 треугольника).
- Из полученных 4 треугольников и малого квадрата (4х4) сложи один квадрат.
Результаты на экране (смотри рис.№12)
Блок 8. Резюме
Учитель: Итак, наш урок подошел к концу, давайте подведем итог нашей работы. Продолжите фразы, которые я буду начинать говорить.
- Сегодня мы узнали на уроке……
- Мы научились……
- Мы пробовали применять……
А теперь ответьте мне на мои вопросы:
- Какие качества вам помогли сегодня на уроке?
- Что особенно понравилось на уроке?
- Что совсем не понравилось?
Оцените сегодняшний урок с помощью трех рожиц (смотри рис.№13):

Ссылки на источники
- Федеральный государственный образовательный стандарт основного общего образования. –М.: Госстандарт России: Издательство стандартов
- Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: Прикладной курс научного творчества: Учебное пособие. - Киров: АНОО «Межрегиональный ЦИТО», 2013. - 212 с
- Зиновкина М. М. Многоуровневое непрерывное креативное образование в школе // Концепт. – 2012. – No 9 (сентябрь). – ART 12116. – 1,0 п. л. – URL: http://www.covenok.ru/koncept/2012/ 12116.htm.- Гос. рег. Эл No ФС 77- 49965. – ISSN 2304-120X.- [ Дата обращения 15.08.2014]
- Зиновкина М. М., Утёмов В. В. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ // Социально-антропологические проблемы информационного общества. Выпуск 1. – Концепт. – 2013. – ART 64054. – URL: http://e-koncept.ru/teleconf/64054.html – Гос. рег. Эл № ФС 77- 49965. – ISSN 2304-120X.[Дата обращения 17.08.2014]
- О.Ю.Едуш. Геометрия 7 класс Подсказки на каждый день – М.Гуманитарный издательский центр «Владос»,2001.-176с
- Утёмов В. В. Адаптированные методы научного творчества в обучении математике // Концепт: научно-методический электронный журнал. – 2012. – № 7 (июль). – ART 12095. – 0,5 п. л. – URL: http://www.covenok.ru/koncept/2012/12095.htm. – Гос. рег. Эл № ФС 77-49965. – ISSN 2304-120X.[Дата обращения 17.08.2014]
- Утёмов В. В. Использование инструментов ТРИЗ в обучении школьников математике // Концепт. – 2011. – 1 квартал 2011. – ART 11101. – URL: http://e-koncept.ru/2011/11101.htm. – Гос. рег. Эл No ФС 77-49965. – ISSN 2304-120X. [Дата обращения: 09.09.2014]