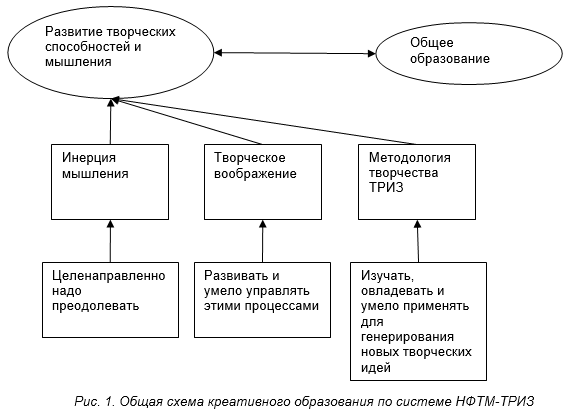
Одним из путей реализации интегративного подхода в школьном образовании является использование методов научного творчества в процессе обучения школьников различным предметам, прежде всего методологией ТРИ3 Г. С. Альтшуллера, что позволяет не учить предмету, а учить предметом, учить делать открытия. Существуют два вида открытий.
В первом случае человек, решая ту или иную проблему, открывает новое знание (проблема идея).
Во-вторых, получив каким-либо образом интересный результат, он пытается выяснить, решением какой проблемы мог бы быть этот результат (идея проблема). «И вот, как это ни кажется парадоксальным, чаще всего встречается второй вид изобретений, и он становится всё более общим по мере развития науки» [1]. В последние десятилетия учёные интенсивно развивают этот подход: идти в открытии не от проблемы, а от потенциальной возможности. Таким образом, в науке выявилась мощная тенденция, которую дидактика не может не учитывать. Обращая схему (идея проблема), мы получаем второй вид открытий учащихся в обучении. Иными словами, сначала ученики каким-либо образом находят идею, а потом уже исследуют, решению какой задачи эта идея могла бы способствовать. В связи с этим возникает основная идея творческого обучения учащихся: сначала организовать продуктивный поиск идей и фактов школьниками, а потом исследовать, где и как можно реализовать полученные результаты.
Методическая (дидактическая) система, направленная на развитие творческого мышления учащихся должна включать в себя оба подхода к обучению. При этом педагог должен учитывать главные дидактические принципы НФТМ-ТРИЗ:
- принцип диагностики личности учащегося и студента, и коллектива учебной группы;
- принцип развития интеллектуальной активности личности;
- принцип развития и воспитания личности через творчество;
- принцип непрерывности творческого развития;
- принцип преемственности творческого развития;
- принцип поисковой деятельности;
- принцип творческой самореализации;
- принцип педагогического сопряжения теории развития творческого мышления со стандартизованной программой;
- принцип сотворчества;
- принцип обучения способам творческой деятельности и ускоренному приобретению опыта решения творческих задач;
- принцип синтеза проблемности и алгоритмизации предметного содержания;
- принцип положительного эмоционального фона;
- принцип предметной интеграции с методологией творчества ТРИЗ;
- принцип формирования системности мышления;
- принцип природосообразности принимаемых решений;
- принцип коммуникативности;
- принцип "Docendo discimus" («Уча – учимся сами»)
- принцип демократизации учебного процесса;
- принцип соревновательности [6].
Такой подход требует и особой организации учебной деятельности. Хорошо вписывается в учебную деятельность для развития креативности учащихся игра с математическими объектами, которая основана на методах теории решения изобретательских задач (ТРИЗ), в обучении учащихся математике. Игра с объектами создаёт базу для продуктивного генерирования идей учащихся. А игра с объектами и идеями не только помогает ученику развить свои творческие способности, но, и направлена на сознательное и глубокое изучение им школьного предмета.
1. По теории ТРИЗ любой объект можно исследовать, изменить, сконструировать, соотнести с другими объектами. На уроках хорошо использовать основные направления игры с математическими объектами:
- Разбиение объекта (дробление, выделение какой-либо части объекта как особенной, вынесение части объекта и игра с ней отдельно, рассмотрение объекта как части другого объекта).
- Изменение объекта (отбрасывание каких – либо элементов объекта, обмен местами элементов объекта, поиск инварианта при изменении объекта, изменение объекта по определённой схеме, соглашение считать неравные элементы равными, произвольные – находящимися в определённом отношении, далёкие – близкими и наоборот).
- Поиск новых свойств и функций объекта (поиск «слабых» свойств объекта, «наделение» объекта новым свойством, поиск новой функции объекта).
- Конструирование объекта (построение объекта с заданными свойствами, построение объектов на базе одного объекта, построение объектов на базе двух объектов, «свободное» конструирование объектов).
- Движение объекта (представление возможности части объекта быть подвижной, укладывание объекта «на бок», переход объекта из одного измерения в другое, движение объекта относительно других объектов).
- Соотнесение объектов (чередование объектов, перенос свойств одного объекта на другие, перенос структуры объекта, присоединение к объекту других объектов, «порождение» объектов нескольких сходных объектов, игра с объектов одной природы по правилам объектов другой природы) [6].
2. Игра с математическими идеями есть интеллектуальная деятельность, направленная на исследование ресурсов той или иной идеи, изменение идей, соотнесение их друг с другом с целью получения новых идей. Ключевая роль в игре с математическими идеями принадлежит учителю. Он организует поисковые ситуации по развитию учащимися идей. Он ненавязчиво направляет поиски школьников, делает прямые и косвенные подсказки, стимулирует их мысль яркими примерами открытий.
Поисковую деятельность учащихся удобно начинать с логических следствий, постепенно переходя на ассоциативные связи, заключения. Методика продуктивной игры с идеями предполагает:
- Развитие идей.
- Соотнесение идей (математические с нематематическими, стратегические с тактическими, по одному принципу).
- Обращение идей (применяется принцип «наоборот»).
- Перенос идей из одной области в другую.
Инновационные педагогические технологии в многоуровневой системе НФТМ-ТРИЗ предусматривают реализацию основных дидактических принципов через изменение структуры уроков и их оригинальное наполнение.
Блок 1 (мотивация) представляет собой специально отобранную систему оригинальных объектов-сюрпризов, способных вызвать удивление учащегося. Этот блок обеспечивает мотивацию учащегося к занятиям и развивает его любознательность.
Блоки 2 и 6 (содержательная часть) содержат программный материал учебного курса и обеспечивают формирование системного мышления и развитие творческих способностей.
Блок 3 (психологическая разгрузка) представляет собой систему психологической разгрузки. Психологическая разгрузка реализуется через упражнения по гармонизации развития полушарий головного мозга, через аутотренинг, через систему спортивно-эмоциональных игр, театрализацию.
Блок 4 (головоломка) представляет собой систему усложняющихся головоломок, воплощенных в реальные объекты, в конструкции которых реализована оригинальная, остроумная идея.
Блок 5 (интеллектуальная разминка) представляет систему усложняющихся заданий, направленных на развитие мотивации, дивергентного и логического мышления и творческих способностей учащихся.
Блок 7 (компьютерная интеллектуальная поддержка) обеспечивает мотивацию и развитие мышления, предусматривает систему усложняющихся компьютерных игр-головоломок, адаптированных к возрасту учащихся, обеспечивает переход из внешнего плана действий во внутренний план.
Блок 8 (резюме) обеспечивает обратную связь с учащимися на уроке и предусматривает качественную и эмоциональную оценку учащимся самого урока [5].
Рассмотрим, как можно построить урок геометрии в 10 классе по теме «Пирамида. Решение задач на свойства пирамиды», применяя математические игры с объектами и идеями.
Блок 1. Мотивация
Решать задачи по геометрии для учеников очень сложно и необходимость создания мотивационной аранжировки уроков состоит в том, что специально продумана система заданий для поддержания устойчивой положительной мотивации в ходе урока. В начале урока надо удивить учеников и урок геометрии можно начать с физического опыта по кипению и испарению воды. Потом задать вопрос: почему и как испаряется вода? (Отдельные молекулы, двигаясь в хаотичном движении, покидают воду и уходят в воздух). Этот образ «выпрыгивающей» молекулы предложить использовать для решения задачи. Пусть точки принадлежат одной плоскости. И одна из точек вдруг поднимается над этой плоскостью. Будут ли сохраняться те свойства, которыми она обладала на плоскости и не приобретёт ли она новые свойства.
