Всвязи с принятием в Российской Федерации Федерального государственного образовательного стандарта начальной, основной и в последующем – в средней школе, ориентированного на компетентностный подход к оценке качества образования, остро встал вопрос о проектировании методик диагностики новых образовательных результатов учащихся. Новый образовательный результат?
- познавательныеи личностные способности ученика;
- компетенциикак способность ученика соорганизовывать ресурсы для достижения цели (знания в действии);
- метапредметные результаты образовательной деятельности (способы деятельности, применимые как в рамках образовательного процесса, так и при решении проблем в реальных жизненных ситуациях, освоенные обучающимися на базе одного, нескольких или всех учебных предметов);
- инициативность, самостоятельность, ответственность как свойства и ресурсы личности, которые обеспечивают успешность личности на протяжении всего жизненного пути;
- универсальные учебные действия ученика.
В рамках РИП группой учителей математики проводится разработка и экспериментальная проверка пакета диагностических методик на оценку метапредметных образовательных результатов и уровня освоения предметных способовдействий учащихся 2-5 классов (в перспективе 2-9). В настоящей работе представлен анализ экспериментальной проверки трех диагностических заданий для оценки метапредметных и предметных результатов (на материале математики) учащихся 10-12 классов вечерней школы города Набережные Челны. Контингент обучающихся школы в настоящее время разнороден по возрасту (от 15 до 40 лет), подготовленности, социальной зрелости, профессиональной направленности и мотивам обучения. Это подростки, ушедшие из дневной школы по разным причинам, работающая молодежь и т. д. Были предложены для решения следующие задачи.
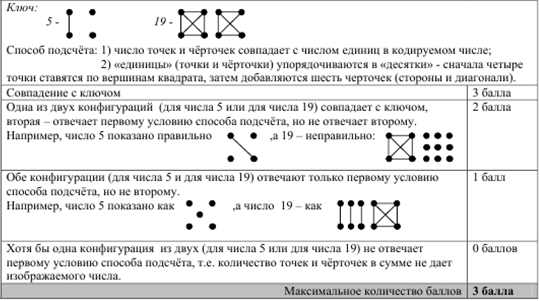
1.Задача «Точки и черточки».
Удобный способ подсчёта количества показан в таблице на примере двух чисел, 3 и 11.
Догадайтесь, как записывают числа с помощью точек и чёрточек. Заполните таблицу
2. Задача «Велосипед». У детского трехколесного велосипеда 2 задних колеса и одно переднее. Заднее колесо вдвое меньше, чем переднее колесо. Какое расстояние проехало каждое колесо, если велосипед переместился на 4 метра по прямой?
3. Задача «Эскалатор». Саша любит считать ступеньки, не пропуская ни одной, когда идёт по эскалатору в метро. Когда он насчитает больше ступенек:если идёт по ходу или против хода эскалатора?
Объясните ответ.
Задача «Точки и черточки» - на проверку:
1. умения создавать, применятьи преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.
2. анализ (выяснить, что такое удобный способ подсчета)
Уровни освоения способа действия:
| Уровень | Название | Характеристика уровня | Диагностические критерии |
|
0
|
начальный | Способ действия не освоен. | Ребенок затрудняется при выполнении типового задания, освоенного на уроках. |
|
1
|
формальный | Овладение внешними особенностями образца действия, ориентация на форму образца. | Ребенок успешно выполняет типовое задание, освоенное на уроках. Затруднения испытывает в случаях, когда условие (особенности) задачи не указывает прямо на тип задачи и не связывается непосредственно с отработанной схемой действия. |
|
2
|
промежуточный | Ориентация на существенное предметное отношение неустойчива. | Промежуточный (между формальным и содержательным) характер выполнения. В части задач поднимается на высоту предметного уровня, в другой части – остается на формальном. |
|
3
|
содержательный | Освоение существенного предметного отношения, лежащего в основе способа действия. | Успешен в реализации способа действия, в том числе в задачах, в которых затруднена ориентация на несущественные для данного класса задач признаки |
Были представлены различныеварианты ответов:
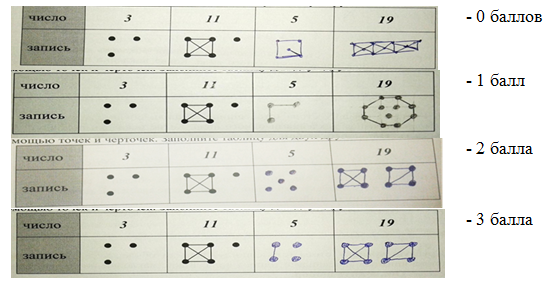 |
На диаграмме 1 представлены данные по результатам выполнения первой задачи.
Диаграмма 1. Распределение всех испытуемых поуспешности выполнения первой задачи.

Большая часть учеников не справилась с выполнением задачи – 38,81%. Задача была довольно таки сложной для учащихся: не многие увидели «десятку»
- сначала ставятся точки по вершинам квадрата, а потом шесть черточек, как стороны и диагонали квадрата. Хотя многие догадались, что число точек и черточек должно совпадать с числом единиц в кодируемом числе.
Задача «Велосипед» - напроверку:
1. умения различатьсущественную и несущественную информацию;
2. начальные формы познавательной рефлексии (умение определять, какого типа задача перед тобой, каким способом она решается).

Были представлены следующие вариантыответов:
 |
|
Диаграмма 2. Распределение всех испытуемых поуспешности выполнения второй задачи. 
Вторая задача «Велосипед» оказалась более легкой для учеников, 69% учащихся справились с задачей на предметном уровне.
Задача «Эскалатор» - задача предметной диагностики на взаимосвязь характеристик движения (скорость, время, расстояние), движение по ходу (по течению) и против хода (против течения). Из задачи исключили цифровые характеристики и нет прямого указания на применение формулы скорости через расстояние и время. Но без знания данной формулы определить, когда же Саша насчитает больше ступенек было бы невозможно.

Были представлены следующие вариантыответов:
 |
|
Диаграмма 3. Распределение всех испытуемых поуспешности выполнения третьей задачи.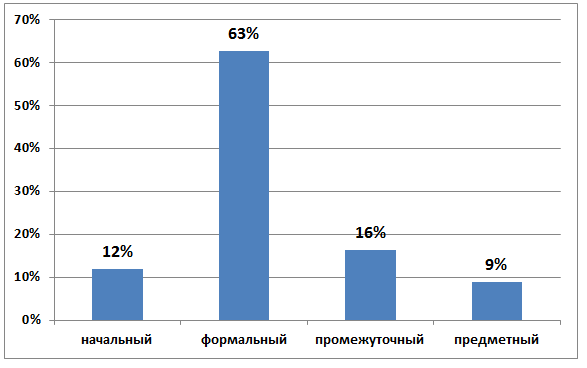
Задача 3 более трудная для учеников, чем задачи 1 и 2. Большая часть учеников справилась с
задачей на формальном уровне (знаю, что против хода, но объяснить не могу).
Рекомендации учителям.
- При проектировании заданий методик диагностики, обычно, мы исходим из предположения, что все ученики действую сознательно, и успешность выполнения заданий определяется уровнем развития соответствующих компетенций. Но нельзя исключать возможность случайного выбора правильного ответа. Лучше давать большее количество однотипных заданий и тем самым уменьшать влияние случайного выбора правильного ответа наконечный результат диагностики.
- При разработке и проверке тематического планирования учитывать наличие и полноту представления всех планируемых результатов.
- Контролировать включение втекущий и этапный контроль заданий различного вида, формы предъявления и уровня трудности.
- Обеспечивать оптимальный объем изучения содержания, соответствующего требованиям планируемых результатов «ученик получит возможность научиться».

