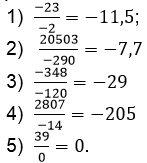Личностные УУД
Задание №1. «Отгадай шифр».
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике, Формировать положительное отношение к процессу познания, формирование личностных качеств: аккуратность при выполнении работы, бережливость, трудолюбие, логическое мышление.
Возраст: 11–15 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: задание носит творческий проектный характер. Задания дают возможность продемонстрировать перед детьми ценность мозгового штурма как формы эффективного интеллектуального взаимодействия. Такая работа развивает у детей представление о толерантности, учит терпению во взаимоотношениях и в то же время умению не терять при общении свою индивидуальность, т.е. также способствует формированию представлений о ценности человеческой личности.
Материалы: карточка с заданием, карандаши.
Инструкция:
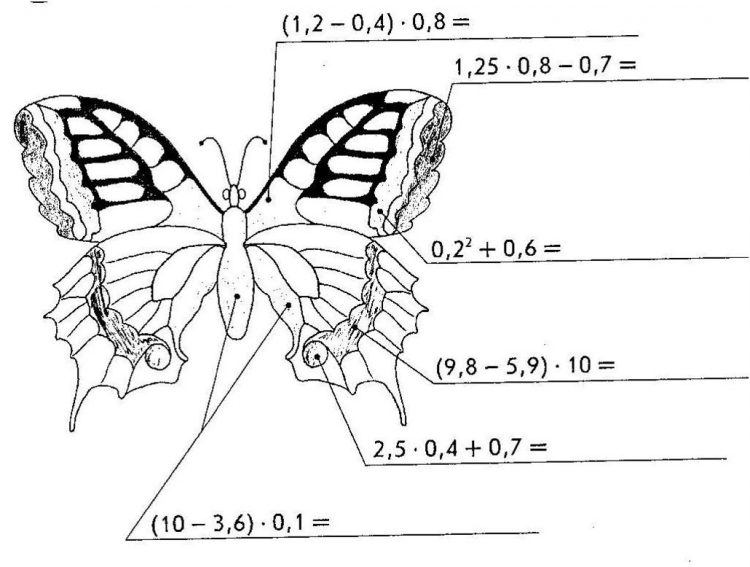
1) Необходимо раскрасить бабочку в цвета, по определенному цвету нужно сначала вычислить значение выражения [1].
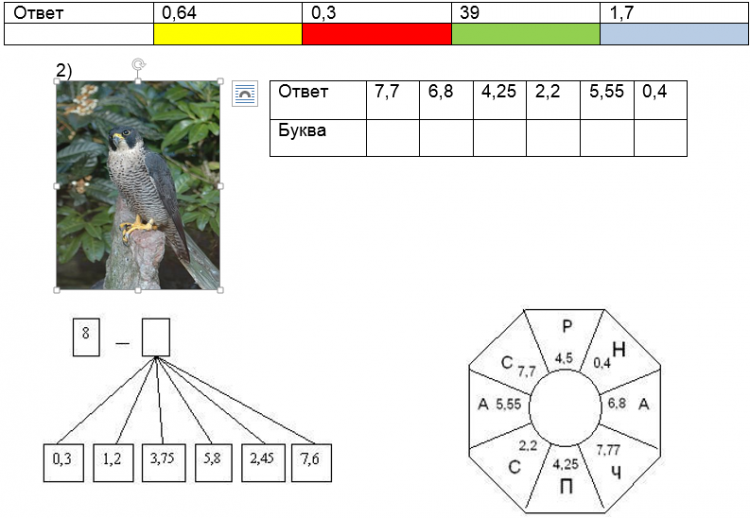
2) Необходимо разгадать название птицы, выполнив действия по схеме, и в таблицу под ответами запишем соответствующие буквы [1].
1)
Критерии оценивания:- правильность вычисления арифметических действий;
- аккуратность в выполнение задания №1.
Задание №2. «Загадки древности»
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике, Формировать положительное отношение к процессу познания, формирование личностных качеств: трудолюбие, логическое мышление, заинтересованность. Знакомство с трудами известных ученых.
Возраст: 11–15 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: задание носит логический характер. Задания дают возможность продемонстрировать перед детьми ценность мозгового штурма как формы эффективного интеллектуального взаимодействия. Задания построены на историческом материале, рассказываю о созидательной работе ученых. Работая с текстами этих задач, учитель не может пройти мимо личностной оценки описанных в них реальных исторических персонажей и ценности личного вклада человека в создание больших человеческих сообществ.
Материалы: карточка с задачами, фотографии известных ученых. (Архимед, Аристотель, Безу, Диофант).
Инструкция: решение задач глубокой древности, представляющих интерес и по сей день.
1) Задача Диофанта (из трактата «Арифметика»)
Требуется число 100 разделить два раза так, чтобы большая часть его от первого деления была вдвое более меньшей части от второго деления и чтобы большая часть от второго деления была втрое более меньшей части от первого деления [2].
2) Задача Архимеда ( из трактата «Леммы»)
Если круг описан около квадрата, а другой в него вписан, то описанный круг, вдвое больше вписанного [2].
3) Задача Безу
Некто купил лошадь и спустя некоторое время продал ее за 24 пистоля. При этой продаже он теряет столько процентов, сколь стоила ему лошадь. Спрашивается, за какую сумму он ее купил? [2]
4) Задача Ньютона ( из «Всеобщая арифметика»)
Некий торговец каждый год увеличивает на одну треть свое состояние, уменьшенное на сто фунтов, которые ежегодно затрачивает на свою семью. Через три года он обнаруживает, что его состояние удвоилось. Спрашивается, сколько у него было денег вначале? [3]
5) Задача Наполеона.
Данную окружность с данным положением центра разделить на равные части при помощи одного циркуля, не прибегая к линейке [3].
Критерии оценивания:
- правильность вычисления арифметических действий;
- способность логического мышления;
- умение прислушиваться к аргументам других участников дискуссии и учитывать их в своей позиции, при решении задачи.
Познавательные УУД
Задание №1. «Знакомство с историей математики»
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике. Формировать положительное отношение к процессу познания, формирование личностных качеств: трудолюбие, логическое мышление, заинтересованность. Научить школьников самостоятельному применению знаний в новой ситуации.
Возраст: 11–15 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: Необходимость формирования моделирования как универсального учебного действия. Для математики это действие представляется наиболее важным, так как создаёт важнейший инструментарий для развития у детей познавательных универсальных действий, этому способствует широкое использование продуктивных заданий, требующих целенаправленного использования и, как следствие, развития таких важнейших мыслительных операций, как анализ, синтез, классификация, сравнение, аналогия [4].
Материалы: карточка с заданием, интернет, энциклопедии по математике.
Инструкция: произвести вычисления в задание, каждому ответу соответствует буква, затем расшифровать имя известного ученого (если решено верно, то получится слово Бхаскары). Используя интернет или дополнительную литературу записать задачу индийского ученого (про обезьян) и ее решить. А затем обсудить решение совместно с учителем или другими учениками класса [4].
Решите уравнения и расшифруйте слово:
Если задание выполнено верно, получим задачу Бхаскары (про обезьян):
Забавляясь, обезьяны на две группы разделились:
Часть восьмая их в квадрате в роще весело резвилась,
А двенадцать хором пели, на любимом сидя месте.
Сосчитай, сколько в роще обезьянок вместе было.
Критерии оценивания:
- правильность вычисления арифметических действий;
- способность логического мышления;
- умение работы с ресурсами интернета, работа с дополнительной литературой;
- умение показать и отстоять правильность полученного решения.
Задание №2. «Математические лабиринты»
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике. Формировать положительное отношение к процессу познания, формирование личностных качеств: трудолюбие, логическое мышление, заинтересованность. Проверка умения и навыков учащихся по данной теме.
Возраст: 11–15 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: «Лабиринт» – это несколько заданий, соединенных таким образом, что ответ одного задания служит номером другого. Выполнив одно задание, следует перейти к другому, и так до тех пор, пока ответ задания не совпадет с его номером. Игра начинается за 15–20 минут до конца урока. Лабиринт рассчитан на самостоятельное решение заданий. В результате решения получается цепочка чисел, по которой, как по ориентиру, ученик выходит из лабиринта. Перечень таких цепочек-чисел для каждого варианта должен быть записан у учителя. Это позволит следить за успешностью прохождения лабиринта отдельными учащимися или командой [5].
Материалы: карточка с заданием.
Инструкция: выполнив одно задание, следует перейти к другому, и так до тех пор, пока ответ задания не совпадет с его номером. В результате решения получается цепочка чисел, по которой, как по ориентиру, ученик выходит из лабиринта. Класс делится на 2 команды либо на 3 (2 или 3 варианта). Номер первого уравнения, которое надо решить, указывает учитель [5].
а) Математический лабиринт по теме: «Решение уравнений», 5–6 класс.
Учащиеся получают бланк с заданием.
Вход в лабиринт: для I варианта с № 1, для II варианта с № 2.
Выход из лабиринта: полученный ответ совпадает с номером задания.
№ 1. Решите уравнение: 25 (у + 56) = 1625
№ 2. Решите уравнение: 28 - t + 35 = 53
№ 3. При каком значении переменной х 8х в 11 раз меньше, чем 264?
№ 4. При каком значении переменной а сумма а и 408 больше числа 312 на 104?
№ 5. При каком значении переменной m 360 в 12 раз больше 6 m?
№ 6. При каком значении переменной у число 661 меньше разности 800 и у на 132?
№ 7. Решите уравнение: 13х + 15х - 24 = 60
№ 8. Решите уравнение: (16х + 3х - х) : 15 = 6
№ 9. Решите уравнение: 528 : а - 24 = 64
№ 10. Решите уравнение: (3722 + р) : 54 = 69
Ключ к лабиринту:
I вариант: 1 —> 9 —> 6 —> 7 —> 3
II вариант: 2 —> 10 —> 4 —> 8 —> 5
б) Математический лабиринт по теме: «Решение уравнений», 7 класс.
Учащиеся получают бланк с заданием:
№ 1. 4 (1 – 0,5а) = -2 (2а – 3)
№ 2. 4 (3 - х) – 11 = 7 (2х – 5)
№ 3. –5 (0,8 а + 1,2) = -а – 18
№ 4. 4 (3х – 8) = 3 (5 – х) + 13
№.5
№ 6
№ 7 -3,2 в + 2,4 = -2 (1,2в + 2,4)
№ 8 = 9
№ 9. 1,2 (3х + 5) = 2 (2,4 х – 3,6)
№ 10. 0,3 (5х – 7) = 3 (0,2х + 3,2)
№ 11. 0,5у – 0,6 = 0,1у + 0,2
№ 12. –3 (2,1х – 4) – 4,2 = 1,2 (-5х + 0,5)
№ 13.
Критерии оценивания:
- правильность вычисления арифметических действий;
- способность логического мышления;
- умение работать в команде;
- умение прислушиваться к аргументам других участников дискуссии и учитывать их в своей позиции, при решении задачи;
- умение показать и отстоять правильность полученного решения.
Регулятивные УУД
Задание №1. «Преднамеренные ошибки»
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике. Формировать положительное отношение к процессу познания, формирование личностных качеств: трудолюбие, логическое мышление, заинтересованность. Развитие внимательности при вычислении, получение навыков по быстрому и эффективному поиску логических ошибок.
Возраст: 11–15 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: Ребятам нравится, когда учитель дает задание на исправление преднамеренных ошибок в решении, на восстановление частично стертых записей. Не попадайтесь такие логические ловушки. Выработка навыка выделения в описании задачи главного и удерживать на нем внимание. Тренировка умения искать ошибки. Решение специальных заданий на выявление ошибок различного уровня и вида: математических, логических, случайных и преднамеренных [3].
Материалы: карточка с заданием.
Инструкция: найти ошибки и исправить их. Объясните, незнание какого материала их повлекло. Подумайте, как можно избежать таких ошибок [3].
Задача про инвалидов.
Инвалиды решили купить себе перчатки, при чем у одного из них нет левой руки, а у другого правой. Продавец продал перчатки за 25 рублей (взял по 12 рублей с каждого), но потом ему стало их жалко – и он решил скинуть им 5 рублей. Пока продавец догонял их, он купил себе попить за 3 рубля, и отдал инвалидам 2 рубля. (по 1 рублю каждому). Получается, что каждый из инвалидов потратил по 11, 5 рублей. Итак, 11,5+11,5 = 23 руб., но продавец купил себе попить за 3 рубля из этих 5 рублей, значит 23+3=26 руб. Вопрос, откуда взялся еще один рубль?
Критерии оценивания:
- правильность вычисления арифметических действий;
- способность логического мышления;
- умение найти и исправить ошибки;
- умение прислушиваться к аргументам других участников дискуссии и учитывать их в своей позиции, при решении задачи;
- умение показать и отстоять правильность полученного решения.
Задание №2. «Взаимоконроль»
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике. Произвести взаимоконтроль уровня знаний, взаимоконтроль осуществляют учащиеся. Взаимоконтроль проводится путем сравнения с образцом, в форме взаимных проверок, в виде консультацией с учителем. Материал для взаимоконтроля обычно готовится учителем, но также может выбираться проверяющим учеником.
Возраст: 11–15 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: ребятам раздаются карточки с заданиями, а также оценочные листы. Задания разделены на блоки, которых может быть от 3–5 по желанию учителя. Блоки рассчитаны на темы, которые были пройдены ранее. После выполнения заданий на карточке, ученики вносят в оценочный лист полученные ответы, затем обмениваются оценочными листами. Начинается проверка. Учитель говорит правильный результат, ученики сравнивают его с тем, который написан на карточке, и в столбике рядом записывают количество баллов за правильность выполнения (от 0 до 5). Каждое правильно выполненное задание оценивается в 1 балл. В оценочном листе учащиеся друг другу выставляют баллы. Затем все баллы суммируются, и по шкале выбирается оценка [6].
Материалы: оценочные листы, карточки с заданиями.
Инструкция: ребятам раздаются карточки с заданиями, а также оценочные листы. После выполнения заданий на карточке, ученики вносят в оценочный лист полученные ответы, затем обмениваются оценочными листами. Начинается проверка. В оценочном листе учащиеся друг другу выставляют баллы. Затем все баллы суммируются, и по шкале выбирается оценка 6].
I тур. Проверка домашнего задания.
II тур. Проверка знаний формул.
1) Два автомобиля ехали навстречу друг другу, Скорость первого автомобиля была х км/ч, а второго – 58 км/ч. Какое расстояние S между ними первоначально, если они встретились через 2 часа?
|
1) S = 2(х+58) км
|
2) S = 2х+ 58 км
|
3) S = 2(х-58) км
|
4) S = (58-х)2 км
|
2) Найдите площадь прямоугольника, ширина которого 200м, а длина на 600м больше. Площадь вырази в гектарах.
|
1) 16 га
|
2) 8 га
|
3) 4 га
|
4) 32 га
|
3) Площадь квадрата равна 196см. Чему равна сторона квадрата?
|
1) 14 см
|
2) 15 см
|
3) 8 см,
|
4) 24 см
|
4) Используя формулу N = х+8y -44, найдите значение N. При х=28, y=18.
|
1) 128
|
2) 144
|
3) 66
|
4) 108
|
Варианты наборов цифр:
1. Лейбниц Готфрид Вильгельм – 1011,
2. Чебышев Пафнутий Львович – 2134,
3. Виленкин Наум Яковлевич – 3412,
4. Павловский Евгений Никанорович – 1111.
ОТВЕТ: Павловский Евгений Никанорович
III тур. Отработка формул через решение задач.
1) Число 102 является членом арифметической прогрессии 10,14,18, … Найти номер этого члена и сумму 10+14+18+…+102 членов этой прогрессии.
2) В геометрической прогрессии b1=9, q =.Найти b4 и сумму четырех первых членов этой прогрессии.
IV тур. Решение задач, повышенной сложности.
1) 20 туристов – мужчины, женщины и дети – вместе несли груз 200 кг. Сколько среди них было детей, если каждый мужчина нес 20 кг, каждая женщина – 5 кг, а каждый ребенок – 3 кг?
2) Можно ли 37 конфет разделить на четверых без остатка?
|
ФИО ученика
|
|
Класс
|
|
Этапы
|
Задания
|
Количество баллов
|
|
I. Проверка домашнего задания (работа в парах, взаимоконтроль)
|
№1
|
|
|
№2
|
|
|
№3
|
|
|
№4
|
|
|
II. Проверка знаний формул (работа в группах, самоконтроль)
|
№1
|
|
|
№2
|
|
|
№3
|
|
|
№4
|
|
|
III. Отработка формул через решение задач.
|
№1
|
|
|
№2
|
|
|
IV. Решение задач, повышенной сложности
|
№1
|
|
|
№2
|
|
|
Ответы на дополнительные вопросы
|
|
|
|
Итоговое количество баллов
|
|
|
Оценка
|
|
Критерии оценивания:
- правильность вычисления арифметических действий;
- умение найти и исправить ошибки;
- умение прислушиваться к аргументам других участников дискуссии и учитывать их в своей позиции, при решении задачи;
- умение показать и отстоять правильность полученного решения.
Коммуникативные УУД
Задание №1. «Интеллектуальный марафон»
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике. Организация учащихся к работе в группе. Управление поведением – контроль, коррекция, оценка действий партнера и своих собственных.
Возраст: 11–15 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: разделить учеников на 2 команды. Учитель выступает в роли ведущего. Один из учеников выбирается в качестве судьи, регистрирует результаты раундов. каждый раунд содержит несложное, логическое задание, рассчитанное на смекалку. После проведения такого своеобразного мозгового штурма подводятся итоги, победившая команда получает поощрение [5].
Материалы: карточки с заданием.
Инструкция: каждая команда получает карточку с заданием, на размышление дается от 2–5 минут в зависимости от сложности задания. По окончании времени командам дается возможность представить полученный результат, в случае правильности присваивается 2 балла, в случае ошибки – 0. В конце игры подводится общий итог. Выявляется команда победитель [5].
1 раунд. Если буквы слова «кенгуру» расположить в алфавитном порядке, какая буква окажется на третьем месте?
2 раунд. Сутки на планете Тамагочи на 40 минут длиннее, чем на планете Земля. На сколько неделя на Тамагочи отличается от недели на Земле?
|
1) 4 ч 40 мин
|
2) 2ч 20 мин
|
3) 7ч 20 мин
|
4) 40 мин
|
5) 28 ч
|
3 раунд. Решите анаграммы:
|
1) чадаза
|
2) гурк
|
3) чул
|
4) мапряя
|
5) резоток
|
4 раунд. Расшифруйте «закодированные» слова:
|
1) и100рия
|
2) про100р
|
3) кис.
|
4) 3тон
|
5) о3цание
|
5 раунд. Вычислите площадь квадрата, периметр которого равен 36 см
|
1) 12 см2
|
2) 18 см2
|
3) 81 см2
|
4) 25 см2
|
|
6 раунд. Выберите самое маленькое четырехзначное число, в записи которого все цифры разные.
|
1) 1023
|
2) 1234
|
3) 1203
|
4) 1032
|
5) 1203
|
7 раунд. Корень уравнения х – 12678 = 25349 равен
|
1) 35428
|
2) 12675
|
3) 38027
|
4) 2671
|
5) 28027
|
8. Найдите значение выражения CXXV – XXXV
|
1) CX
|
2) CXI
|
3) IC
|
4) IICV
|
5) XC
|
Критерии оценивания:
- правильность вычисления арифметических действий;
- способность логического мышления;
- умение прислушиваться к аргументам других участников дискуссии и учитывать их в своей позиции, при решении задачи;
- умение показать и отстоять правильность полученного решения.
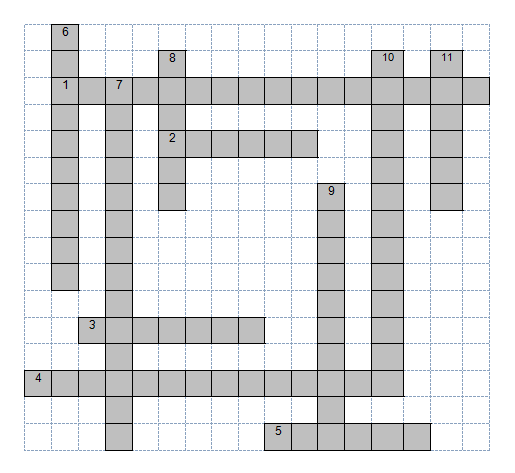
Задание №2. Кроссворд на тему «Треугольник»
Цель: включение школьников в эту интеллектуальную игру, позволяет учителю в нетрадиционной форме проверить их знания, прочность и глубину усвоения пройденного, выявить, какие именно вопросы нуждаются в разъяснении и закреплении.
Возраст: 11–15 лет.
Форма выполнения задания: групповая работа.
Описание задания: разделить учеников на 2 команды. задача каждой команды составить кроссворд на тему «Треугольник». Кроссворд должен содержать как можно больше слов по заданной теме. Также при оценивание будет учитываться оригинальность формы кроссворда [1], [5].
Материалы: лист бумаги.
Инструменты: каждая команда получает лист бумаги, на размышление дается от 20–25 минут. По окончании времени листочки с конструкцией кроссворда и вопросами собираются и передаются команде соперников. Командам дается 10 минут на заполнение кроссворда. Затем листочки собираются, по результатам проверки определяется команда победителей [1], [5].
По горизонтали:
- Прямые, пересекающиеся под прямым углом.
- Признак равенства треугольников (по стороне и двум прилежащим к ней углам).
- Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
- Треугольник с равными сторонами.
- Признак равенства треугольников (по трем сторонам).
По вертикали:
- Сторона треугольника, противолежащая прямому углу.
- Треугольник с двумя равными сторонами.
- Признак равенства треугольников (по двум сторонам и углу между ними).
- Длина перпендикуляра, опущенного из данной точки на прямую.
- Треугольник с прямым углом.
- Перпендикуляр, проведенный из вершины треугольника на противоположную сторону.
Критерии оценивания:
- способность логического мышления;
- умение прислушиваться к аргументам других участников дискуссии и учитывать их в своей позиции, при решении задачи;
- умение показать и отстоять правильность полученного решения.
Ссылки на источники
- Коваленко В. Г. Дидактические игры на уроках математики. – М: Просвещение, 1990 г.
- Чистяков В. Д. Сборник старинных задач по элементарной математике с историческими экскурсами и подробными решениями. – Минск: Министерства высшего, среднего специального и профессионального образования БССР, 1962.
- Энциклопедический словарь юного математика / Сост. Э-68 А. П. Савин. – М.: Педагогика, 1989.
- Сборник для подготовки к ГИА под редакцией Ф. Ф. Лысенко Учебник «Алгебра 9», авторы Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и другие.
- Дышинский Е. А. Игротека математического кружка (Пособие для учителя). М.: Просвещение, 1972.
- Утеева Р. А. Групповая работа как одна из форм деятельности учащихся на уроке // Математика в школе, 1985, № 2.
Skvortsova Daria Andriivna,
teacher of mathematics. School № 61. Magnitogorsk
darya_sc_90@mail.ru
Typical tasks in the formation of universal learning activities in math class
Abstract: The article presents the tasks that contribute to the formation of universal educational activities (personal, educational , regulatory , communication) in mathematics lessons in 5-8 classes by means of different types of problems, examples, games, creative tasks.
Keywords: universal learning activities, learning to learn, assignments, math games, practice skills.