О том, как стремительно новая технология решения творческих задач (ТРИЗ) завоевывает мир, можно судить по всемирной компьютерной сети Интернет. За последние годы количество статей по ТРИЗ уже превысило несколько тысяч. Крупнейшие мировые корпорации ищут специалистов для своих изобретательских и исследовательских служб.
Как сама теория, так и методология преподавания ТРИЗ непрерывно развиваются. Идеи и методы переносятся на нетехнические области: художественные системы, менеджмент, управление коллективами, рекламу, решение коммерческих, социальных, социально-технических и педагогических задач, задач системы образования.
Система обучения с использованием ТРИЗ-технологий охватывает все возрасты, начиная с детского сада. Ребенок, владеющий элементами ТРИЗ, может сам решать свои проблемы, причем нестандартно, неординарно. Вот простой, но наглядный случай. Мальчик восьми лет оказался перед дверью, закрытой сестрой изнутри. Как войти в комнату? Применить силу? Поднять крик? Он сформулировал идеальное решение: сестра сама должна открыть дверь! Мальчик подошел к двери и крикнул сестре: «Я тебя запер!» Через несколько секунд она сама распахнула дверь, освобождая себя из «плена».
Инженер, владеющий ТРИЗ, имеет возможность эффективно развивать и совершенствовать технические системы. У педагога, использующего даже элементы теории, дети занимаются с увлечением, без перегрузок осваивают новые знания, развивают речь и мышление, осваивают иностранные языки без зубрежки.
Сценаристам и писателям технологии развития творческого воображения помогают придумывать сюжеты произведений, описывать фантастические объекты. Бизнесмены, владеющие ТРИЗ, обходят конкурентов и повышают свои доходы за счет более эффективного использования имеющихся ресурсов. ТРИЗ-технологии позволяют объединить усилия специалистов разного профиля при разработке и реализации крупных программ, избежать дорогостоящих ошибок [1].
Современная школа выполняет государственный заказ. Цель школьного образования сегодня – развитие креативной, творческой личности путем включения учащегося в различные виды деятельности, его личностное саморазвитие и самоопределение. Укротив дикую лошадь, человек стремительно начал осваивать новые пространства суши. Укротив с помощью парусов ветер, он начал осваивать новые континенты. ТРИЗ-технологии позволяют человеку осваивать возможности собственного мышления [1].
Методы теории решения изобретательских задач формируют у детей умение творчески разрешать возникшие проблемы, способствуют отхождению от стандартных решений, т. е. помогают преодолевать инерцию в мышлении. Эта инновационная технология содержательно и методологически соответствует требованиям ФГОС основного общего образования, способствует достижению личностных и метапредметных результатов обучения, позволяет создавать образовательное поле, в котором происходит формирование нового творческого типа личности. Она формирует инициативную позицию, вдохновляет учеников на новые открытия, наводит на творческие мысли, заставляет рассуждать, доказывать, предлагать оригинальные идеи, сочинять, изобретать. Активно раскрываются творческие способности детей, повышается самооценка. Всё выше перечисленное воспитывает успешных, активных, творчески мыслящих людей, затребованных современным обществом [2].
Концепция креативности, как феномена творчества, была введена в науку американским психологом Дж. Гилфордом. В конце 50-х годов прошлого века он сформулировал несколько критериев креативности:
- Беглость мысли – количество идей, возникающих за некоторую единицу времени, легкость генерирования идей.
- Гибкость мысли – способность переключаться с одной идеи на другую.
- Оригинальность – способность производить идеи, отличающиеся от общепринятых стереотипов, способность отвечать на раздражители нестандартно (не путать оригинальность мышления с оригинальничанием).
- Любознательность – чувствительность к проблемам, к окружающим ситуациям, восприимчивость – чувствительность к необычным деталям, противоречиям и неопределенности, готовность быстро переключаться с одной идеи на другую.
- Способность к разработке гипотезы – смелой идеи, которая потом нуждается в обстоятельной эмпирической проверке.
- Удовлетворенность – итог проявления креативности, – логическая независимость реакций от стимулов, способность решать проблемы, способность к анализу и синтезу [3].
Таким образом, креативность – это творческие способности индивида, характеризующиеся готовностью к созданию принципиально новых идей, отклоняющихся от традиционных или принятых схем мышления и входящие в структуру одаренности в качестве независимого фактора. По определению Г. С. Альтшуллера «Каждый ребёнок изначально талантлив и даже гениален, но его надо научить ориентироваться в современном мире, чтобы при минимуме затрат достичь максимум эффекта» [2].
Главная задача учителя – развивать творческую мыслительную деятельность ребенка, научить учащихся не обращать внимания на шаблонность мышления, быть уверенней и не бояться выдвигать самые невероятные идеи. А это возможно благодаря внедрению в образовательный процесс особых технологий развития креативного мышления, таких как развивающее обучение, технологии ТРИЗ, технология игрового моделирования, метод проектов, разноуровневое обучение, информационно-коммуникативные технологии, проблемное обучение, диалоговые технологии [4].
Связь образовательных результатов с используемыми современными образовательными технологиями, развивающими креативное мышление, хорошо прослеживается при рассмотрении таблицы [5].
Креативная деятельность развивает личность ребенка, помогает ему усваивать моральные и нравственные нормы. Создавая произведение творчества, ученик отражает в них свое понимание жизненных ценностей, свои личностные свойства. Взрослый человек, часто критически оценивая свои творческие способности, стесняется их проявлять. В. А. Сухомлинский писал «Дети должны жить в мире красоты, игры, сказки, музыки, рисунка, фантазии, творчества» [6]
Таблица 1
|
Технология
|
Результат использования технологии
|
|
Развивающее обучение
|
Формирование умения и желания учиться, развитие инициативности, интереса к учению.
|
|
Разноуровневое обучение
|
Разработка разноуровневых заданий. Комплектование групп обучения в соответствии с индивидуальными возможностями. Вовлеченность в учебную деятельность всех учащихся.
|
|
Проблемное обучение
|
Обеспечение активного характера педагогического процесса. Создание условий для развития учащихся посредством учебного предмета. Формирование у учащихся умения видеть проблему, формулировать её, искать варианты решения, комбинировать разные аналитические подходы, версии, позиции, синтезировать их, формулировать выводы.
|
|
Технология обучения в сотрудничестве
|
Выработка навыков групповой учебно-поисковой деятельности, совместный поиск и выработка нового знания, освоение нового опыта
|
|
Технология учебно-поисковой деятельности
|
Развитие исследовательских навыков в процессе обучения с последующей презентацией результатов работы в виде: реферата, доклада, сообщения, отчета
|
|
Проектные методы обучения
|
Формирование исследовательских, информационных, коммуникативных компетенций. Создание условий для организаторской деятельности и сотрудничества.
|
|
Информационно-коммуникативные технологии
|
Повышение эффективности урока за счет использования мультимедиа средств, Интернет-технологий. Формирование общих и специальных информационных и коммуникативных компетенций.
|
|
Технология игрового моделирования
|
Повышение эффективности урока, качества усвоения учебного материала учащимися за счет возможности в творческой обстановке сформировать и закрепить знания, умения, навыки. Формирование исследовательского и творческого отношения к действительности. Реализация потребности личности учащегося в самовыражении, самоопределения, саморегуляции. Усиление здоровьесберегающего аспекта предметного обучения
|
|
Диалоговые технологии (учебная дискуссия; диспут)
|
Обеспечение субъект-субъектных отношений в процессе обучение. Углубление уровня понимания учебного материала. Развитие личностных качеств, необходимых для эффективного общения (умения вступать в дискуссию и вырабатывать своё собственную позицию, слушать)
|
Развитие креативного мышления на уроках математики и в межпредметных связях осуществляется через:
- разрешение проблемных ситуаций;
- изложение различных точек зрения на один и тот же вопрос;
- побуждение делать анализ, сравнение, обобщение, сопоставление фактов, вывод;
- постановку творческих задач;
- применение исследовательского проектного методов.
Развитию креативного мышления способствуют проблемные ситуации с применением следующих методических приемов:
- обсуждение различных вариантов решений одной и той же задачи;
- знакомство с различными точками зрения по одной проблеме;
- предложение учащимся заданий по поиску интересных интеллектуальных задач;
- обучение учащихся самостоятельному конструированию логических задач.
Математика начинается не со счета, а с загадки, проблемы. Обучение творчеству имеет важный социальный аспект. Если школьник с самого начала своей ученической деятельности подготавливается к тому, что он должен учиться создавать, придумывать, находить оригинальные решения задач, то формирование личности этого школьника будет отличаться от того, как формируется личность ребенка, обучаемого в рамках идеологии повторения, сказанного учителем. «Не накормить голодного рыбой, а научить ее ловить!» Цель любого преподавателя – организовать обучающий процесс так, чтобы дать ученику возможность и мотив самостоятельной исследовательской работы. А вот задача ученика – самому прийти к истине.
Мыслительные операции, способствующие развитию
креативного мышления
I. Важнейшими математическими операциями являются анализ и синтез.
– Анализ связан с выделением элементов данного объекта, его признаков или свойств.
– Синтез – соединение различных элементов, сторон объекта в единое целое.
В мыслительной деятельности анализ и синтез дополняют друг друга. Формированию и развитию данных мыслительных операций способствует решение задач, в которых от учащихся требуется проводить правильные рассуждения, рассматривать объекты с разных сторон, указывать их различные и схожие свойства, а также ставить различные вопросы относительно данного объекта.
Приведем примеры таких заданий для учащихся 5-6 классов:
1. Какой знак надо поставить между 7 и 8, чтобы получилось число больше 7, но меньшее 8?
2. Два мотоциклиста едут навстречу друг другу. Скорость одного из них равна (в км/ч) площади прямоугольника со сторонами 31 и 2. Скорость другого мотоциклиста составляет 10 % от 540. Через сколько часов мотоциклисты встретятся, если сейчас между ними расстояние, равное (в км) количеству кубиков с ребром, равным 1, составляющих прямоугольный параллелепипед с измерениями 29, 4 и 3?
3. Задача из рассказа А. П. Чехова «Репетитор».
Купец купил 138 аршин черного и синего сукна за 540 р. Спрашивается: сколько аршин купил он того и другого, если синее стоило 5 р. за аршин, а черное 3 р?
4. Пользуясь цифрами от 1 до 9 и знаками действий, напишите число 100, выполняя условие, что цифры надо писать по порядку.
5. (Старинная задача) Собака усмотрела в 150 саженях зайца, который пробегает в 2 минуты по 500 сажен, а собака в 5 минут – 1300 сажен. Спрашивается, в какое время собака догонит зайца?
II. Другой мыслительной операцией, способствующей развитию креативных способностей учащихся, и которой должны овладеть ученики, является сравнение. Формированию приема сравнения способствуют задания, в которых требуется сравнить объекты, указать их признаки и свойства, найти сходства и различия.
1. Что общего у этих фигур? (дается девять фигур, составленных из 10 геометрических фигур и, например, изображающих фигуру человека).
Изображают фигуру человека.
Фигура составлена из 10 элементов.
Среди элементов – треугольники, круги, квадраты.
2. Укажите лишнюю фигуру? Круг – единственная фигура, которая не имеет углов.
Квадрат – единственная фигура, имеющая четыре прямых угла.
Треугольник – это единственный несимметричный объект.
Сектор – единственная из всех фигур, которая содержит и прямые линии, и кривые.
Полумесяц – единственная фигура, которая имеет выемку.
Каждая из фигур чем-то отличается от всех других, но в то же время все они в равной степени имеют признаки, которые их объединяют.
III. Развитию креативности способствует и аналогия. Использование аналогии в математике является одним из основных методов при поиске доказательства теоремы, решении текстовых задач. Для формирования умения проводить аналогию можно использовать задачи на нахождение словесных аналогий, аналогий между различными объектами.
Например, по аналогии с первой парой подберите недостающее слово в другой паре:
1) влево – вправо, вверх – …
2) сумма – сложение, частное – …
3) квадрат – куб, круг – …
4) уменьшаемое – вычитаемое, делимое …
Такие упражнения развивают воображение учащихся и играют немалую роль в формировании креативности мыслительной деятельности. Кроме того, систематические упражнения такого рода дают возможность усвоить алгоритм нахождения аналогов – по функциям, по признакам, по подсистемам.
IV. Классификация – следующий прием мышления, способствующий развитию креативности. Суть его в разбиении множества рассматриваемых явлений или объектов на попарно пересекающиеся подмножества. Подобные задачи способствуют развитию умения «узнавать» знакомые объекты, переносить знания в непривычную ситуацию, видеть структуру объекта. Например, найдите «лишнее» число: 1,5; 6,3; 48; 0,9; 1,2.
V. Обобщение говорит о степени развития мыслительной деятельности, осознанности, прочности усвоения и объеме знаний учащихся.
Например, дайте общее название объектам, входящим в одну группу:
а) разность, частное – это…
б) 8; 4; -2; 11; 16; -13 – это…
в) прямая, треугольник – это…
VI. Решение задач – головоломок, ребусов, занимательных задач, задач на смекалку так же способствует развитию креативности. При выполнении таких задач учащимся чаще всего приходится пользоваться методом проб и ошибок, что в конечном счете развивает интуицию, творчество, способность искать другой способ решения, отказавшись от ложного пути. Поиск решения таких задач воспитывает усидчивость, развивает различные виды памяти, внимание,
VII. Развитие креативности, умения самостоятельно конструировать свои знания лежит и в основе метода проектов.
Полезность проекта заключается в том, что мы не рассказываем ребенку ничего лишнего. У него есть право выбора первого шага, хода и даже цели проекта. Идя к этой цели, он сталкивается с тем, что ему приходится «добывать» знания, а затем соединять разрозненные сведения. Он черпает из разных предметных областей только необходимые знания и использует их в той деятельности, которая ему интересна [7].
Пример урока математики в 5 классе, разработанного в структуре «креативный урок» [8]. Тема урока «Геометрические тела». УМК – авторы И. И. Зубарева, А. Г. Мордкович.
Дать первичные представления о геометрических телах
1. Систематизировать знания учащихся о геометрических телах.
2. Формировать понятие «геометрическое тело», «развертка», умения сопоставлять название тела и его внешний вид, называть элементы (вершина, ребро, грань).
3. Формировать навыки изображения геометрических тел, выполнения их моделей, решения логических задач
Личностные: целостное восприятие окружающего мира, начальные представления о роли математики в системе знаний.
Предметные: умение работать в информационном поле (таблицы, схемы, диаграммы, графики, последовательности, цепочки, совокупности); представлять, анализировать и интерпретировать данные.
Метапредметные:
– владение основными методами познания окружающего мира (наблюдение, сравнение, анализ, синтез, обобщение, моделирование); развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости компьютера;
– умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности; умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач; формирование и развитие компетентности в области использования информационно-коммуникационных технологий.
Познавательные УУД: формирования у учащихся функциональной грамотности – умения воспринимать и критически анализировать информацию, представленную в различных формах.
Регулятивные УУД: принимать и сохранять учебную задачу; адекватно оценивать свои достижения.
Коммуникативные УУД: участвовать в диалоге, выполняя принятые правила речевого поведения; уметь строить свои.
Блок 1. Мотивация
Проверка готовности к уроку. Учитель просит ребят открыть тетради, записать дату и нарисовать дом, магазин, клуб или какое-либо другое здание.
(Предполагается, что дети выберут стандартную форму – параллелепипед).
Учитель просит ребят показать друг другу, что у кого получилось, и ответить на вопрос «Похожи ли рисунки, и чем?» (Метод сравнения)
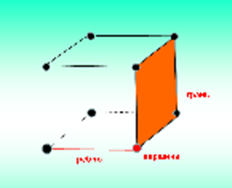
Тогда учитель проецирует на экран возможные варианты зданий (рис. 1) – этап удивления.
Рис. 1
– Видели ли вы когда-нибудь подобные здания? Где? (Возможно дети встречались с такой архитектурой во время путешествий).
– Часто ли можно видеть такие сооружения в нашем поселке? А в современных городах? (Не очень, но встречаются. И это здорово! Это необычно! Это креативно!)
Блок 2. Содержательная часть
Формы каких геометрических тел вы увидели на фотографиях?
(Пирамида, шар, цилиндр)
Сегодня мы с вами попытаемся разобраться, что это за тела? Почему называются телами? Чем похожи? Чем отличаются?
- Работа с учебником. Откройте учебники на стр. 233.
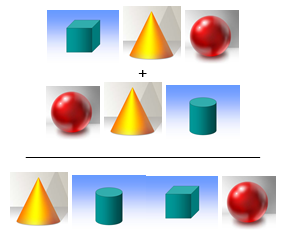
Рис. 2.
Рассмотрите фигуры на рисунке и объясните, почему они выделены в две группы? Чем он отличаются? (Введение понятий многогранник, круглое тело – тело вращения)
Какую геометрическую фигуру надо вращать, чтобы получить: конус; цилиндр; шар?
– Какие общие элементы у многогранников и тел вращения? (вершина, основание)
– Что есть у многогранников и нет у тел вращения? (грани, ребра)
Рассмотрение элементов: вершина, грань, ребро, основание.
Рис. 3.
Работа с рис. 144 в учебнике на стр. 234.
Задача № 908
Маша сказала: «Я думаю, не обязательно пересчитывать ребра и вершины прямоугольного параллелепипеда, чтобы узнать их число. Можно рассуждать так: параллелепипед имеет 6 граней, каждая грань 4 ребра, значит параллелепипед имеет 24 ребра. Аналогично получаем 24 вершины». Найдите ошибки в рассуждениях Маши.
Задача № 909.
Рис. 4.
Какой формы основание у пирамиды? Наша пирамида треугольная.
А может ли основание быть другой формы? Какой? Как тогда можно назвать пирамиду?
Блок 3. Головоломка
1) Куб окрасили и разделили на маленькие кубики, словно кубик-рубик. Сколько не окрашенных вовсе кубиков получилось? У скольких окрашена 1 грань, 2 грани, 3 грани? 4 грани?
Рис. 5.
2) На какое геометрическое тело похож гладкий карандаш? А шайба?
Задание группам.
1 группа: У вас 5 таких карандашей. Расположите их так чтобы каждый одновременно касался четырех других. Сколько способов расположения вы нашли?
2 группа: Заменим шайбу шашкой. Расположите 5 шашек так, чтобы каждая касалась четырех других.
Блок 4. Психологическая разгрузка
Музыкальная физкультминутка http://www.youtube.com/watch?v=y-Y9Le52OAg.
Блок 5. Интеллектуальная разминка
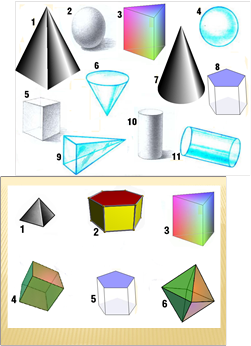
Замените тела цифрами и прочитайте слово, пользуясь кодом.
Рис. 6.
Таблица 2
|
Нет ни граней, ни ребер, ни вершин
|
Получается, если вращать треугольник
|
Так еще называется шляпа
|
Как ни катай, а все равно не катится
|
|
р
|
к
|
г
|
у
|
Восстановите логическую цепочку:
Круг – окружность, шар – … (сфера),
Биллиардный – шар(ик), теннисный или воздушный ….(сферик)
Блок 6. Содержательная часть
Работа над понятиями вид справа, сверху, снизу, сверху, видимые невидимые элементы, развертка.
- Задания № 911, рис.146-148 учебника
- Рабочая тетрадь № 2, № 51.2, стр. 57, № 51.5, стр. 59.
Блок 7. Компьютерная интеллектуальная поддержка
Закрепление материала. На доске через проектор появляются рисунки геометрических фигур. Задача учеников назвать номера называемых фигур или наоборот описывают тело, номер которого называет товарищ.
Рис. 7.
Домашнее задание: п. 50, 51, вопросы, № 910, 925, рабочая тетрадь, стр. 58. № 51.3.
Блок 8. Резюме «И дело в шляпе»
Учащимся предлагается оценить свое эмоциональное состояние на уроке, оживив смайлик (изобразив ему мимику) и опустить его в шляпу символизирующую его настроение, объяснить выбор (Что понравилось, чему научился, почему скучал и т. п.)
Таблица 3
Заключение. С появлением НФТМ-ТРИЗ в образовательной практике у учителя появилась уникальная возможность управлять процессом мышления и творчества себя и своих учеников. Эта система одна из передовых современных технологий решения проблем, направленных на получение предельно мало затратных решений высшего уровня. Овладев основными мыслительными операциями по созданию творческого продукта, вам захочется учить и учиться, мыслить и творить, мечтать и претворять свои мечты в реальность.
Ссылки на источники
- www.trizland.ru.
- Книга «Психология творчества, креативности, одаренности», с.30, http://www.kodges.ru/static/read_56894_30_73.html.
- Н. В. Лупилина Использование ТРИЗ на уроке математики в условиях реализации ФГОС.
- http://si-sv.com/load/7-1-0-34.
- Анализ современных образовательных технологии, способствующих развитию креативного мышления. Формирование банка технологий, http://do.gendocs.ru/docs/index-353421.html.
- Степанюк И. В. Формирование креативного мышления на уроках // Молодой ученый. – 2015. – № 16. – С. 426–428.
- http://izlov.ru/docs/100/index-18882.html
- Утёмов В. В., Зиновкина М. М. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ // Современные научные исследования. Выпуск 1. - Концепт. - 2013. - ART 53572. - URL: http://e-koncept.ru/2013/53572.htm - ISSN 2304-120X.