Структура креативного урока по схеме целостной системы многоуровневого непрерывного креативного образования НФТМ-ТРИЗ М. М. Зиновкиной отличается от традиционного урока и включает в себя блоки, реализующие цели занятия, адекватные целям креативного образования в целом [1].
Блок 1 (мотивация). В этой части урока ребенок встречается с чем-то в той или иной степени поражающим его воображение. Для всех креативных уроков она обеспечивается специально отобранной системой оригинальных объектов – сюрпризов, способных вызвать удивление учащегося. Этот блок обеспечивает мотивацию учащегося к занятиям и развивает его любознательность.
Блоки 2 и 6 (содержательная часть) содержат программный материал учебного курса и обеспечивает формирование системного мышления и развитие творческих способностей.
Блок 3 (психологическая разгрузка) представляет собой систему психологической разгрузки. Психологическая разгрузка реализуется через упражнения по гармонизации развития полушарий головного мозга, через аутотренинг, через систему спортивно-эмоциональных игр, театрализацию и др.
Блок 4 (головоломка) представляет собой систему усложняющихся головоломок, воплощенных в реальные объекты, в конструкции которых реализована оригинальная, остроумная идея.
Блок 5 (интеллектуальная разминка) представляет систему усложняющихся заданий открытого типа, направленных на развитие мотивации, дивергентного и логического мышления и творческих способностей учащихся.
Блок 7 (компьютерная интеллектуальная поддержка) обеспечивает мотивацию и развитие мышления, предусматривает систему усложняющихся компьютерных игр-головоломок, адаптированных к возрасту учащихся, обеспечивает переход из внешнего плана действий во внутренний план.
Блок 8 (резюме) обеспечивает обратную связь с учащимися на уроке и предусматривает качественную и эмоциональную оценку учащимся самого урока [2].
Ход урока
Блок 1. Мотивация
В начале урока учитель мотивирует учащихся на занятие, предложив упражнение на преодоление инерции мышления.
На доске пишется три примера, учитель спрашивает у класса, могут ли эти примеры быть верными? Почему?
I+I=2
I+I=II
I+I=10
Учащиеся могут назвать ошибочным как третий, так и вместе второй с третьим. Но римская система счисления должна быть знакома учащимся и, если не вспомнят сами, можно дать небольшую подсказку.
Дальше выслушать объяснения, почему ученики считают ошибочным третий пример. После этого учитель говорит, что все три примера верны и задача учеников в середине урока объяснить, почему. Примеры остаются на доске.
Блок 2. Содержательная часть
Основные понятия: позиционная система счисления, цифра, алфавит, основание системы счисления.
В чем отличие первого от второго примера?
Рассмотреть отличие позиционной и непозиционной систем счисления на примере записи любого числа в римской и в десятичной системах счисления.
15810 и CLVIIIримская
Ученики сами формулируют отличия, результаты оформляются на доске в таблице:
Таблица 1
Отличия позиционных и непозиционных систем счисления
|
|
Непозиционная система счисления |
Позиционная система счисления |
|
Значение цифры |
неизменно |
Зависит от положения в числе |
|
Максимально возможное для записи число |
Ограничено количеством цифр системы |
Нет ограничения, бесконечно большое |
Для объяснения дальнейшего материала воспользуемся методом аналогии. На доске записывается ряд примеров:
1+9=10
Что происходит в первом примере? Правильно, цифры десятичной системы счисления закончились и происходит переход в новый разряд.
1+8=10
Что происходит в этом примере? Ученики проводят аналогию, предположив, что цифры закончились и поэтому появляется новый разряд. Тогда сколько всего цифр в данной системе счисления? Исправляем пример, подписывая систему счисления
1+8=10 (9)
Записываем еще несколько примеров, попросив учеников самих объяснить, что он значит и какая это система счисления:
1+7=10
1+6=10
Теперь вернемся к примеру 1+1=10. Учащиеся объясняют, какая это система счисления.
Блок 3 (психологическая разгрузка)
Вопрос классу: «Знаете ли вы, почему арабские цифра записываются именно таким образом? Раньше они были чуть более острыми». Учитель зарисовывает на доске 0 и 1 из рисунка 1. Почему они писались именно так, есть идеи?
Дорисовываем цифру 2, 3 и так пока ученики не назовут закономерность – каждая цифра обозначает число по количеству углов в ней: 0 – нет углов, 1 – один угол, 2 – два угла и т.д.
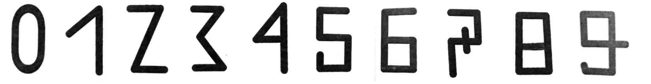
Рис. 1. Древнее написание арабских цифр
А теперь задача учеников изобразить руками или всем телом цифру, которую учитель назовет. Стоя возле рабочих мест, показываем по очереди 0, 1, 2 и т. д. Выбираем самый удачный способ показать цифры.
Теперь усложним задачу, нужно показать у доски число 18564, пример 100+1=…, 1000-91=….
Блок 4. Головоломка
Игра «Ханойский башни» довольна известна. Сыграем с учениками в быстрый вариант головоломки с тремя и четырьмя дисками.
Правила игры:
Есть 1 пирамидка с дисками разного размера, и еще 2 пустые пирамидки. Надо переместить диски с одной пирамидки на другую. Перекладывать можно только по одному диску за ход. Складывать диски можно только меньший на больший.
Итак у нас есть вот такая пирамидка (рис. 2).
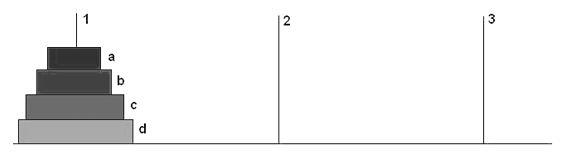
Рис. 2. Ханойские башни (вариант с пятью дисками)
Пронумеруем диски сверху вниз числами 1, 2, . . . , n так, что наименьший диск имеет номер 1, а наибольший — n. Понятно: чтобы переместить диск n, нужно сначала перенести n − 1 меньших дисков, лежащих на нем, на второй стержень. Если это уже сделано (предположим, что это так), то путь для диска n свободен, и мы выполняем его перемещение на третий стержень. После этого остается перенести n − 1 меньших дисков со второго стержня на третий (обратно на диск n), и в итоге вся наша башня окажется на третьем стержне [3].
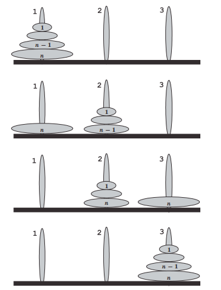
Рис. 3. Логика решения задачи о Ханойских башнях
При изучении программирования целесообразно вернуться к этой задаче и составить алгоритм для ее программного решения.
Блок 5. Интеллектуальная разминка.
В 5 блока используются два фокуса с угадыванием, основанные на двоичной системе счисления из учебного пособия «Занимательная информатика» [4].
Фокус 1. Волшебная таблица
Посмотрите на рисунок 3, с помощью этой таблицы можно отгадать любое задуманное число, не большее 31, если задумавший это число скажет, в каких столбцах таблицы оно встречается (номера столбцов указаны в первой строке таблицы). Например, если задумано число 22, то по названным номерам столбцов (5, 3 и 2) его можно вычислить так: 25–1 + 23–1+ 22–1 = 16 + 4 + 2 (это можно сделать, даже не глядя на таблицу). В чем же секрет «волшебной» таблицы? Найдите ответ на этот вопрос.
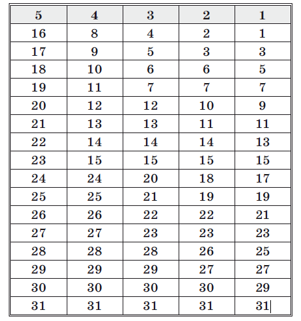
Рис. 4. Волшебная таблица
Фокус 2. Угадаем слово
Учитель спрашивает учеников: «Как вы думаете, а смогу ли я угадать загаданное вами слово?»
Возьмем 15 терминов из информатики. Покажем список ученикам.
- Бит
- Системный блок
- Диск
- Монитор
- Принтер
- Джойстик
- Сканер
- Байт
- Логика
- Система счисления
- Мышка
- Цифра
- Число
- Разряд
- Программа
Также на доску выводятся четыре таблицы:
Таблица 2
|
1 |
|
Сканер Число Логика Бит Принтер Программа Диск Мышка |
Таблица 3
|
2 |
|
Сканер Система счисления Программа Мышка Системный блок Дискета Разряд Джойстик |
Таблица 4
|
3 |
|
Цифра Число Монитор Принтер Джойстик Сканер Программа Разряд |
Таблица 5
|
4 |
|
Цифра Байт Разряд Логика Система счисления Программа Число Мышка |
- В чем же секрет фокуса? Ученики должны найти ответ на этот вопрос.
- Составить собственную такую таблицу для 6 слов. Протестировать ее в мини-группах.

- Зиновкина М. М. Многоуровневое непрерывное креативное образование в школе // Концепт. – 2012. – № 9 (сентябрь). – ART 12116. – 1,0 п. л. – URL: http://www.covenok.ru/koncept/2012/12116.htm. – Гос. рег. Эл № ФС 77- 49965. – ISSN 2304-120X.
- Зиновкина М.М. НФТМ-ТРИЗ: Креативное образование ХХ1 века. Теория и практика. - М.: МГИУ, 2008. - 306 с.
- Ханойские башни [Электронный ресурс] / С. М. Окулов, А. В. Лялин. — 2-е изд. (эл.). — Электрон. текстовые дан. (1 файл pdf : 248 с.). — М. : БИНОМ. Лаборатория знаний, 2015. — (Развитие интеллекта школьников). ISBN 978-5-9963-2810-9
- Златопольский Д.М. Занимательная информатика: учебное пособие. –М.: Бином. Лаборатория знаний, 2011. – 424с.
