Задачи урока.
1. Образовательные:
- закрепление программных знаний и умений по решению тригонометрических уравнений;
- обобщение и систематизация материала;
- создание условий для контроля и самоконтроля усвоения знаний и умений.
2. Воспитательные:
- воспитание навыков делового общения, активности;
- формирование интереса к математике и ее приложениям.
3. Развивающие:
- формирование умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию,
- развитие познавательного интереса, математического кругозора, мышления и речи, внимания и памяти.
Формы организации работы обучающихся на уроке:
индивидуальная, фронтальная, парная, групповая.
Методы обучения:
Частично-поисковый (эвристический), работа по опорным схемам, работа по обобщающей схеме, системные обобщения, самопроверка, взаимопроверка.
Оборудование и источники информации: компьютер, мультимедийный проектор, таблицы «Значения тригонометрических функций некоторых углов», «Тригонометрические формулы»,системно-обобщающая схема (приложение 1);
на партах обучающихся: памятка по решению тригонометрических уравнений, справочные материалы, листы - консультации, лист бумаги для самостоятельной работы, карточки заданий с уравнениями, разноуровневые карточки с домашним заданиям, учебник «Алгебра и начала математического анализа. 10-11 классы.» Задачник для учащихся общеобразовательных учреждений (базовый уровень)/ под ред. А.Г. Морковича.
Ход урока
I. Организационный момент. Озвучивание целей урока и плана его проведения. Мотивация.
Цель: обеспечить внешнюю обстановку для работы на уроке, психологически настроить обучающихся к общению.
Эпиграф занятия: «Без уравнения нет математики как средства познания природы» (академик Александров П. С.).
II. Актуализация опорных знаний. Фронтальный опрос.
Цель: установить уровень знаний и осознанность их применения в рамках изученного теоретического материала, повторение пройденного материала.
1.Опрос по теоретическому материалу:
1.Опрос по теоретическому материалу:
а) Сформулировать определение арксинуса числа.
б) Сформулировать определение арккосинуса числа.
2. Устная работа практической направленности.
1) Вычислите:
1) Вычислите:

2) Имеет ли смысл выражение (ответ объясните):
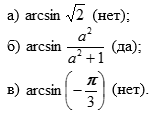
3. Опрос по теоретическому материалу:
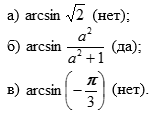
3. Опрос по теоретическому материалу:
А.Эйнштейн говорил так: « Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
1) Какое уравнение называется тригонометрическим?
(Тригонометрическим уравнением называется уравнение, в котором переменная содержится только под знаком тригонометрической функции. Тригонометрическое уравнение либо не имеет корней, либо имеет их бесконечное множество.)
2) Какие уравнения называются тригонометрическими простейшими уравнениями?
(Уравнения sin x=a, cos x=b, tg x=c, ctg x=d называются простейшими тригонометрическими уравнениями)
3) Каковы решения данных уравнений:


4.Устная работа практической направленности.
Исправьте ошибки в решениях тригонометрических уравнений и подумайте об их причинах.
Исправьте ошибки в решениях тригонометрических уравнений и подумайте об их причинах.

III. Проверка домашнего задания.
Цель: установить уровень знаний и осознанность их применения в рамках изученного теоретического материала, повторение пройденного материала.
Два студента работают над заданиями домашней работы у доски.
№ 1

IV. Организация разнообразных упражнений по формированию и совершенствованию практических умений и навыков.
1этап.
Цель: закрепить решение простейших тригонометрических уравнений.
Самостоятельная работа студентов с последующей взаимопроверкой. Работа в парах.
Работа выполняется на листах бумаги с копиркой.
Текст ответа студенты пишут на двойной тетрадном листочке через копирку. Верхний листочек студент, после окончания работы, сдаёт преподавателю на проверку, а по второму осуществляется взаимоконтроль.
1 вариант 2 вариант

Во время самостоятельной работы обучающимся, которые плохо разобрались с данной темой предлагаются листы-консультанты. Лист-консультант состоит из чередования трех блоков:
- Опорная формула, написанная цветными чернилами.
- Решенные примеры.
- Решение примеров самостоятельно.
Студенты сдают первый экземпляр работы, по второму экземпляру осуществляется контроль в ходе взаимопроверки (правильные ответы записываются на обратной стороне доски). Выполняется работа над ошибками.
2 этап.
Цель: закрепить умения решать тригонометрические уравнения методом сведения к квадратному.
Указания преподавателя.
Метод сведения к квадратному состоит в том, что, пользуясь изученными формулами, надо преобразовать уравнение к такому виду, чтобы какую-то функцию (например, sin x или cos x) или комбинацию функций обозначить через y, получив при этом квадратное уравнение относительно y. Разберем несколько примеров:
1) 

3) Решение уравнения самостоятельно с последующей самопроверкой (правильное решение на слайде презентации)
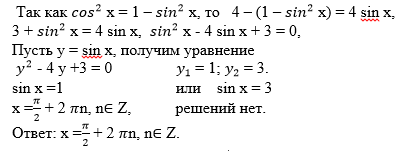
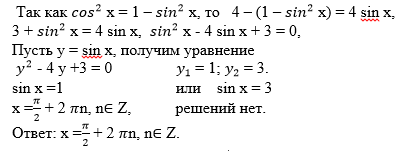
4) Решение уравнений из учебника № 18.8, два студента у доски разбирают решение.
3 этап.
Цель: закрепить навык решения тригонометрических уравнений методом разложения на множители.
Под разложением на множители понимается представление данного выражения в виде произведения нескольких множителей. Если в одной части уравнения стоит несколько множителей, а в другой – 0, то каждый множитель приравнивается к нулю. Таким образом, данный множитель можно представить в виде совокупности более простых уравнений.
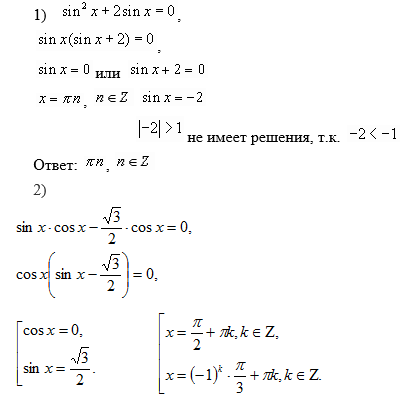
3) Решение уравнений из учебника № 18.11, два студента у доски разбирают решение.
V.Творческое применение и добывание знаний в новой ситуации (проблемное задание)
Работа в группах. Группа, решившая уравнение раньше всех, защищает свое решение.
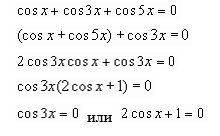
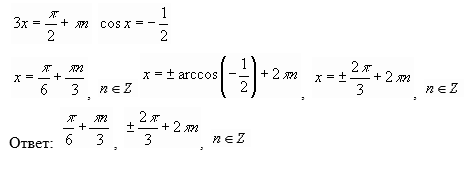
VI. Информация о домашнем задании, инструктаж по его выполнению. Разноуровневая домашняя работа (обучающийся сам определяет уровень).
VII. Рефлексия (подведение итогов занятия).
Цель: вспомнить основные моменты урока, проанализировать усвоение предложенного материала и умение применить полученные знания в дальнейшем
Содержание этапа:
Подведем итоги урока. Сегодня на уроке мы вспомнили понятие арккосинуса, арксинуса, вспомнили формулы решения простейших тригонометрических уравнений, способы решения некоторых известных тригонометрических уравнений. У меня появилась уверенность, что с решением тригонометрических уравнений домашней работы большинство из вас справится.
Фронтальным опросом вместе с обучающимися подводятся итоги урока:
- Что нового узнали на уроке?
- Испытывали ли вы затруднения при выполнении самостоятельной работы?
- Какие пробелы в знаниях выявились на уроке?
Оцените.
Я познание сделал своим ремеслом”
Сосчитайте суммарное количество баллов. Баллы переведите в отметку
30 – 24 балла – «5»
23 – 18 баллов – «4»
Если меньше 18, то отметки не ставить.
Отметьте в карточке: Достигли ли вы цели? Поднимите руки, кто достиг цели, поставленные в начале урока. Спасибо. Молодцы!
Приложение 1


