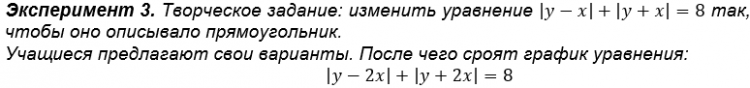Тема урока: Графики уравнений, содержащих символ модуля.
Предмет: алгебра.
Тип урока: комбинированный.
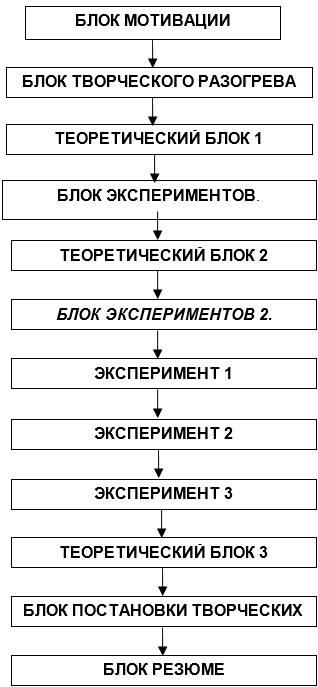Рис. 1. Блок-схема урокаПродолжительность занятия: 90 минут.
Главная дидактическая цель урока: выявление области приложения темы «График уравнения» в алгебре и в её связи с геометрией, формирование знаний по данной теме при решении стандартных и нестандартных алгебраических задач. Развитие у учащихся навыков исследовательской работы.
Цели урока:
- Формирование умений распознавать стандартные задачи в различных формулировках.
- Формирование способности к интеграции знаний из различных тем курса математики.
- Содействовать развитию логического мышления учащихся, умение выделять главное, обобщать.
- Формирование исследовательской, креативной работы учащихся.
- Воспитание графической культуры учащихся.
- Совершенствование коммуникативной культуры учащихся.
Оборудование: доска, мультимедийное оборудование, раздаточный дидактический материал для учащихся.
План урока
1. Блок мотивации. Изучая темы «Графики функций» и «Векторы», мы обнаруживаем тесную связь геометрии и алгебры, и, естественно, возникает вопрос – нельзя ли геометрические фигуры такие как квадрат, прямоугольник, ромб, треугольник задавать алгебраическими уравнениями и иследовать свойства этих фигур алгебраическими методами. Выявлению этой связи между геометрией и алгеброй и будет посвящён урок. Мы введём новое понятие «График уравнения» и рассмотрим графики уравнений в алгебраических и графических задачах. (3 мин.)
2. Блок творческого разогрева. Повторение определения функции и графика функции. Обсуждение необходимости введения понятия «График уравнения».
Устная работа (20 мин.)
Актуализация знаний учащихся: повторение, анализ, обобщение.
Работа учащихся в следующих режимах: диалог, обсуждение, самостоятельная деятельность.
Материалы для проведения устной работы оформлены на доске.
Повторение определения функции и графика функции.
На доске представлены следующие чертежи (Рис. 2).
Каждый ученик получает раздаточный материал с этими чертежами.
Обсуждение:
1) На каких чертежах представлены графики функций? Почему?
2) Графики каких функций представлены на этих чертежах?
3) На каких чертежах графики не задают функции? Почему?
Обсуждается необходимость введения понятия графика уравнения.
Определение: Графиком уравнения называют множество точек координатной плоскости, координаты которых удовлетворяют заданному уравнению.
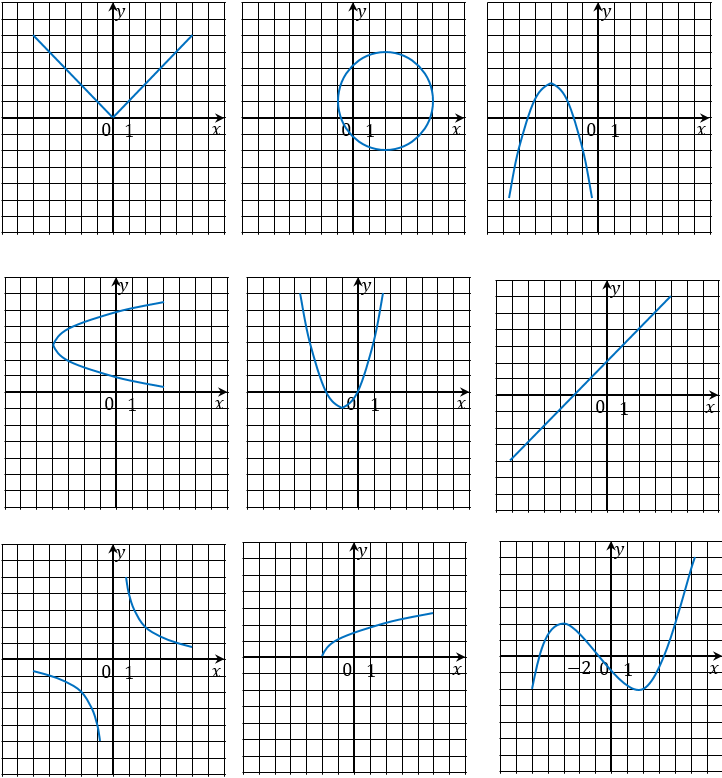Рис. 2.3. Теоретический блок 1. Изображение множества точек, координаты которых удовлетворяют заданным условиям. Ведущие идеи: симметрия, сдвиг графика уравнения (Рис. 3).
Рис. 3.
Обсуждается наилучший способ построения графика этого уравнения.
Варианты:
1. Решить задачу “в лоб”: раскрыть модули в четырёх случаях:
1. Решить задачу “в лоб”: раскрыть модули в четырёх случаях:
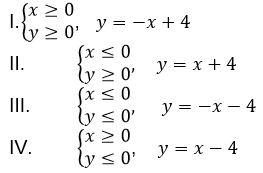
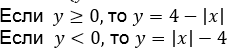
3. Замечаем, что переменные
входят в уравнение симметрично.
Так как, то график уравнения должен быть симметричным как относительно оси , так и относительно оси
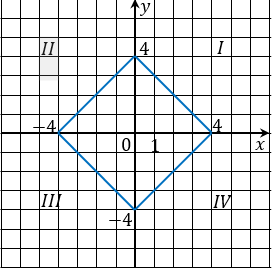Рис. 4
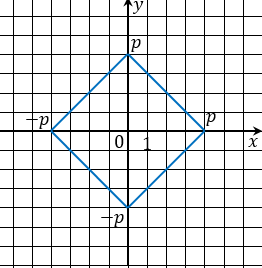Рис. 5 4. Блок экспериментов.
Эксперимент. Преобразовать уравнение которое описывает квадрат так, чтобы уравнение задавало ромб.
Гипотеза: уравнение должно иметь вид:
После обсуждения учащиеся получают задание на два варианта:
Построить графики уравнений:
Рис. 6 Рис. 7
Рис. 8.
Гипотеза: график уравнения получается из графика уравнения в результате сдвига на две единицы вправо вдоль оси и на две единицы в отрицательном направлении вдоль оси График уравнения будет представлять собой квадрат, центр симметрии которого находится в точке Осями симметрии квадрата будут прямые
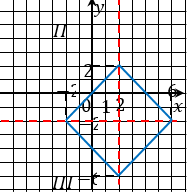
Рис. 9.
Выполняется непосредственная проверка гипотезы. Раскрываются модули в четырёх случаях:
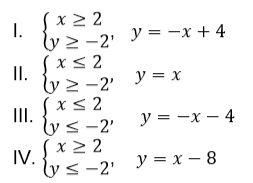
6. Блок экспериментов 2.
Эксперимент 1. Построить график уравнения:
Рассматриваем четыре случая:
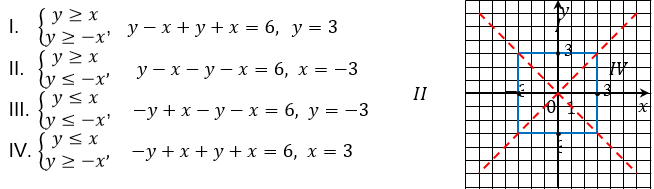
График уравнения представляет собой квадрат центром симметрии которого является точка сторона Рис. 10.
которого а площадь .
Рис. 11.
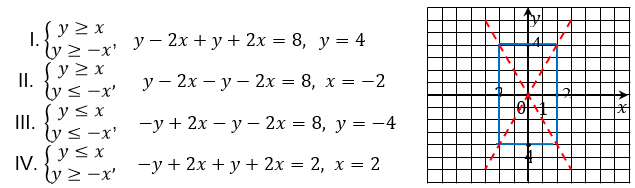
Рис. 12
7. Теоретический блок 3. Методика применения полученных знаний и навыков при решении уравнений некоторых типов с модулем и параметром.
Задание: Решить уравнение
При решении уравнений и неравенств с одним неизвестным, содержащих параметр, удобно проводить исследование на координатно-параметрической плоскости (Значение параметра будем откладывать по вертикальной оси, а значение неизвестного по горизонтальной оси).
Построим на плоскости график данного уравнения. Для этого построим прямые и , которые разобьют плоскость на 4 части.
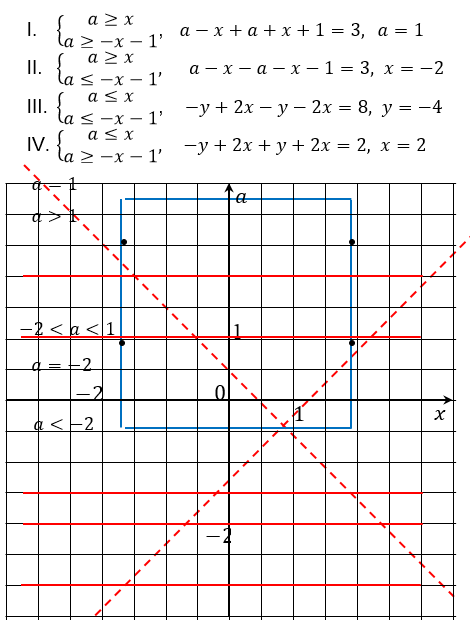
Рис. 13
8. Блок постановки творческих задач.
Обсуждение и комментарии к домашнему заданию (7 мин.).
Домашнее задание к следующему уроку будет содержать:
1) Обязательная часть (индивидуальная работа) (Рис. 14).
Рис. 14.
При решении задания 4 допускается совместное творчество.
2) Творческая часть (допускается совместное творчество) (Рис. 15).
Рис. 15.
Учащиеся должны построить графики этих уравнений и убедиться в том, что одно уравнение описывает параллелограмм, а второе – треугольник. Учащимся предлагается поэкспериментировать с этими уравнениями, меняя коэффициенты при неизвестных, и понаблюдать как это влияет на геометрию получаемых геометрических фигур. Результаты этой самостоятельной работы учащиеся смогут продемонстрировать на следующем уроке.
Блок резюме.
1. Учащиеся формулируют главные выводы урока:
- Дано определение графика уравнения в сравнении с определением графика функции.
- Научились строить графики уравнений, содержащих символ модуля.
- Установили связь геометрии с алгеброй: различные геометрические фигуры могут быть заданы алгебраическими уравнениями. В частности, были построены квадрат, ромб и прямоугольник.
- Познакомились графическим методом решения уравнений с модулем и параметром, с использованием навыков полученных при построении графиков уравнений.
2. Оценивание работы учащихся: самооценка, взаимооценка, оценка работы учащихся учителем.
3. Выяснение мнения учащихся об уроке.
3. Выяснение мнения учащихся об уроке.
Ссылки на источники
- А. Г. Мордкович, Н. П. Николаев Алгебра 9. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2013.
- И. Ф. Шарыгин. Факультативный курс по математике 10. – М. «Просвещение», 1989.
- В. Г. Болтянский, Ю. В. Сидоров, М. И Шабунин. Лекции и задачи по элементарной математике. Издательство “Наука”, М. 1974.