Международная программа по оценке образовательных достижений учащихся PISA, являющаяся мониторинговым исследованием качества общего образовании, отвечает на вопрос «Обладают ли подростки, получившие обязательное общее образование, знаниями и умениями, необходимыми им для полноценного функционирования в современном обществе, т. е. для решения широкого диапазона задач в различных сферах человеческой деятельности, общения и социальных отношений. Последнее исследование 2012 года было сфокусировано на математической грамотности.
Математическая грамотность – это способность индивидуума формулировать, применять и интерпретировать математику в разнообразных контекстах. Она включает математические рассуждения, использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления.
Результаты международных сопоставительных исследований PISA показывают отставание российских подростков от сверстников из большинства развитых стран мира по ключевым для формирования функциональной грамотности направлениям, в том числе по владению умениями применять полученные знания на практике. Российские школьники страдают, по мнению психологов, «выученной беспомощностью» – когда дети попросту теряют способность мыслить и относиться к обучению творчески [1].
Ответом на исследования PISA 2012 г. в России стало Распоряжение Правительства РФ от 24 декабря 2013 г об утверждении Концепции развития математического образования в Российской Федерации, цель которой вывести российское математическое образование на лидирующее положение в мире. Изучение и преподавание математики, с одной стороны, обеспечивают готовность учащихся к применению математики в других областях, с другой стороны, имеют системообразующую функцию, существенно влияют на интеллектуальную готовность школьников и студентов к обучению, а также на содержание и преподавание других предметов [2].
Считаю, одним из условий реализации цели Концепции развития функциональной грамотности является использование на уроках математики и внеурочной деятельности ТРИЗ-технологии Г. С. Альтшуллера. По определению Г. С. Альтшуллера «Каждый ребёнок изначально талантлив и даже гениален, но его надо научить ориентироваться в современном мире, чтобы при минимуме затрат достичь максимум эффекта» [3]. Методы ТРИЗ формируют у детей умение творчески решать возникшие проблемы, способствуют отхождению от стандартных решений, т. е. помогают преодолевать инерцию в мышлении.
Эта инновационная технология содержательно и методологически соответствует требованиям ФГОС НОО второго поколения, способствует достижению личностных и метапредметных результатов обучения, позволяет создавать образовательное поле, в котором происходит формирование нового творческого типа личности [4]. Она даёт вдохновения ученикам на новые открытия, наводит на творческие мысли, заставляет творить, сочинять, изобретать. Учащиеся учатся рассуждать, доказывать, предлагать оригинальные идеи. Активно раскрываются творческие способности детей. У ребёнка происходит формирование инициативной позиции, улучшается самооценка и самоуважение. Всё выше перечисленное воспитывает успешных, активных, творчески мыслящих людей, затребованных современным обществом.
В статье приведён пример использования методов и приёмов НФТМ-ТРИЗ при обучении алгебры в 7-ом классе. Разработка урока в 7-ом классе по теме «Линейная функция» содержит основные этапы креативного урока.
Блок 1 (мотивация) представляет собой специально отобранную систему оригинальных объектов-сюрпризов, способных вызвать удивление учащегося. Этот блок обеспечивает мотивацию учащегося к занятиям и развивает его любознательность.
Сегодняшний урок мы проводим в честь линейной функции. А если какое-то мероприятие проводится в честь кого-то, а в нашем случае в честь чего-то, то это уже (учащиеся могут подсказать) … бенефис. Итак, сегодня урок-бенефис линейной функции.
Мы завершаем тему «Линейная функция», поэтому на уроке вы должны будете продемонстрировать свои знания в честь «Линейной функции». Для начала я приглашаю вас вспомнить некоторые факты. Проводится фронтальный опрос:
– Что такое функция?
– На каком рисунке изображен график функции?
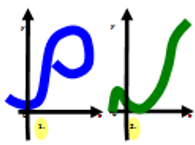 Рис. 1.
Рис. 1.– Что такое область определения функции?
– Найдите область определения функции
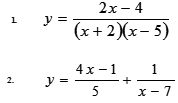
– По графику функции найдите:
1) её область определения;
2) область значений функции.
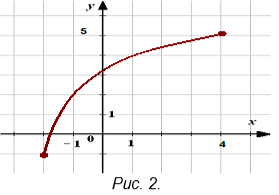
Рис. 2.
На каком рисунке изображён график прямой пропорциональности? Ответ объяснить.
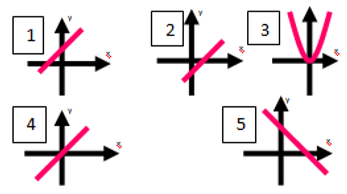 Рис. 3.
Рис. 3.- Выберите формулы, которые задают линейную функцию:
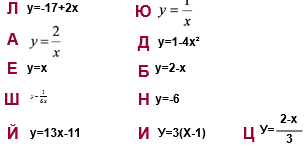 Рис. 4.
Рис. 4.– Итак, правильный ответ – Лейбниц. Кто это? Тогда давайте посмотрим по слайду, какое отношение к функции имеет Лейбниц (краткая биографическая справка о Лейбнице, о его вкладе в развитие понятия «Функция»).
Блок 2 (содержательная часть) содержит программный материал учебного курса и обеспечивают формирование системного мышления и развитие творческих способностей.
– Молодцы! В честь Линейной функции были показаны неплохие знания!
– Ну, а теперь вперёд, за новыми знаниями!
– Напомните, что является графиком линейной функции? Правильно – прямая.
– А теперь мысленно перенесёмся в геометрию. Вспомним, как на плоскости могут располагаться две прямые? (заслушиваются ответы учащихся)
– Итак, две прямые могут пересекаться, быть параллельны и совпадать.
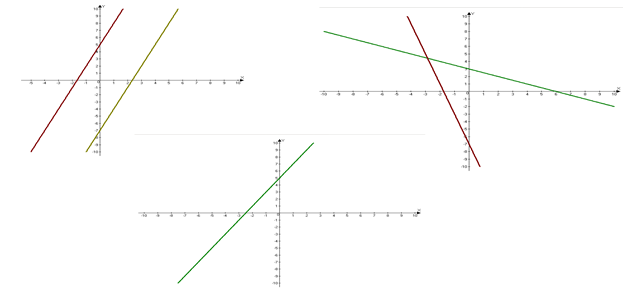 Рис. 5.
Рис. 5.– Как вы думаете, что же может влиять на расположение прямых на плоскости?
(заслушиваются гипотезы ребят)
– Итак, вернёмся обратно в алгебру и проверим ваши предположения, изучив тему взаимное расположение прямых.
– Для этого проведём лабораторную работу, цель которой выяснить, как влияют коэффициенты k и b линейной функции на их взаимное расположение.
– Повернёмся к мониторам. На всех компьютерах загружена, уже знакомая нам, вспомогательная программа AGrapher, в которой мы и будем рисовать прямые. У каждой группы на столе лежит листок с заданиями и указаниями.
– Вам придется выполнить 3 задания на построение разных прямых, по 2 эксперимента в каждом, и записать выводы в конце каждого задания. Сначала выполните первое задание, покажите готовность к заслушиванию выводов.
Лабораторная работа
Задание № 1
а) В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 1
|
Функция |
Коэффициент k |
Коэффициент b |
|
k1= |
b1= |
|
|
k2= |
b2= |
б) В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 2
|
Функция |
Коэффициент k |
Коэффициент b |
|
k1= |
b1= |
|
|
k2= |
b2= |
Вывод: Графики двух линейных функций, заданных формулами вида y=kx+b______________________, если коэффициенты k и b__________________________
Учащиеся делают эксперименты, записывают выводы, некоторые выводы заслушиваются.
– Итак, обобщите (учащиеся должны прийти к выводу: если коэффициенты k1 и k2 в двух линейных функциях различны, коэффициенты b1 и b2 различны, то прямые у=k1x+b1 и y=k2+b2 пересекаются).
– Приступаем ко второму заданию.
Задание № 2
а) В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 3
|
Функция |
Коэффициент k |
Коэффициент b |
|
у=-2x+3 |
k1= |
b1= |
|
у=4x-7 |
k2= |
b2= |
б) В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 4
|
Функция |
Коэффициент k |
Коэффициент b |
|
k1= |
b1= |
|
|
k2= |
b2= |
Вывод: Графики двух линейных функций, заданных формулами вида у=kx+b, ______________________ если коэффициенты b_______________ и коэффициенты k__________________.
– Итак, если все группы справились со вторым заданием, то проверим ваши выводы.
(Заслушивается несколько выводов)
– Итак, если коэффициенты k1 и k2 в двух линейных функциях одинаковы, коэффициенты b1 и b2 различны, то прямые у=k1x+b1 и y=k2+b2 параллельны.
– Ну, и приступаем к последнему 3 заданию.
Задание № 3
а) В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 5
|
Функция |
Коэффициент k |
Коэффициент b |
|
У=10х+8 |
k1= |
b1= |
|
у=3х+8 |
k2= |
b2= |
|
у=0,5х+8 |
k3= |
b3= |
Запишите вывод:
при одинаковом значении коэффициента ___________ все прямые пересекают ось Оу в точке с координатами ( ; )
б) В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 6
|
Функция |
Коэффициент k |
Коэффициент b |
|
у=-4х-5 |
k1= |
b1= |
|
у=-7х-5 |
k2= |
b2= |
|
у=-0,9х-5 |
k3= |
b3= |
Запишите вывод:
при одинаковом значении коэффициента ___________ все прямые пересекают ось Оу в точке с координатами ( ; )
Вывод: Если коэффициенты ________ одинаковы, то точка пересечения графиков линейных функций, заданных формулами вида у=kx+b лежит на оси Оу.
– Все группы справились с последним заданием, проверим ваши выводы.
(Заслушивается несколько выводов)
– Итак, если коэффициенты b1 и b2 одинаковы, то прямые у=k1x+b1 и y=k2+b2 пересекаются в точке с координатами (0;b), т.е. лежит на оси Оу.
– Теперь мы знаем условия параллельности и пересечения двух прямых. А в каком случае прямые будут совпадать?
– Правильно, если коэффициенты k1 и k2 двух линейных функциях одинаковы, коэффициенты b1 и b2 одинаковы.
– Отключаем мониторы.
– Давайте упорядочим полученные знания. Я начинаю, а вы продолжаете.
– Прямые параллельны, если…
– Прямые пересекаются, если…
– Прямые совпадают, если…
– Прямые пересекаются в точке, лежащей на оси ординат, если…
Блок 3 (психологическая разгрузка) представляет собой систему психологической разгрузки. Психологическая разгрузка реализуется через упражнения по гармонизации развития полушарий головного мозга, через аутотренинг, через систему спортивно-эмоциональных игр, театрализацию и др.
– Наша помощница мышка предлагает нам, особенно нашим глазам, немного отдохнуть! Встаем!
(Гимнастика для глаз по слайдам презентации в музыкальном сопровождении.)
– Садимся! И снова встаем, пересаживаемся так, чтоб I вариант оставался за монитором, а II вариант – пересаживается за парты.
Блок 4 (интеллектуальная разминка) представляет систему усложняющихся заданий, направленных на развитие мотивации, дивергентного и логического мышления и творческих способностей учащихся.
Отряд французских солдат во время похода в Алжире очутился однажды в местности, совершенно лишенной растительности и притом с почвой настолько болотистой, что, хотя по ней и можно было ступать, сесть на неё было совершенно невозможно. Усталый отряд продвигался вперед в поисках подходящего места для привала, но на десятки вёрст простиралась всё та же болотистая почва. Как отдохнуть, если нет кругом ни единого сухого местечка и ничего такого, что можно было бы подложить или на что можно было бы сесть?
И всё-таки одному солдату пришла в голову счастливая мысль, которая помогла отряду выйти из затруднительного положения. Солдаты уселись и отдохнули.
Как? Отгадайте!
Для решения ребята объединяются в четыре группы по 6 человек, используя приём «мозгового штурма», т. к. его достоинствами являются сравнительная простота и доступность, быстрота генерирования идей, способных стать основой для серьёзного поиска решения.
Блок 5 (содержательная часть)
Работаем по слайдам.
Задание № 1
Выясним взаимное расположение прямых:
1) у = - 2х – 1 и у = - 2х + 5;
2) у = - 0,5х и у = 0,5х - 3;
3) у = - х – 4 и у = -х - 4;
Задание № 2
Линейная функция задана формулой
Каким графикам будет параллелен график данной функции?
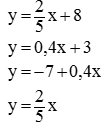
Задание № 3
Задать формулой функцию, график которой параллелен прямой у=-8х+11 и проходит через начало координат
1. у=-8х+1
2. у=-8х
3. у=8х
4. у=11х
Задание № 4
Две прямые пересекаются в точке А (0;4), тогда какое число нужно вставить
у =-11х+4
у = 3х +….
Задание № 5
На рисунке изображены графики функций. Укажите, какая формула соответствует каждому из них.
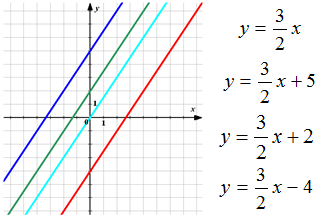
Блок 6 (компьютерная интеллектуальная поддержка) обеспечивает мотивацию и развитие мышления, предусматривает систему усложняющихся компьютерных игр-головоломок, адаптированных к возрасту учащихся, обеспечивает переход из внешнего плана действий во внутренний план.
Сейчас учащиеся первого варианта включают мониторы и приступают к выполнению творческого задания: построение рисунка в координатной плоскости с помощью графиков кусочной линейной функции.
- х=2, -5≤у≤5
- х=-2, -5≤у≤5
- у=2, -5≤х≤5
- у=-2, -5≤х≤5
- у=3-х, -2≤х≤5
- у=х-3, -2≤х≤5
- у=-х-3, -5≤х≤2
- у=х+3, -5≤х≤2
Блок 7 (головоломка) представляет собой систему усложняющихся головоломок, воплощённых в реальные объекты, в конструкции которых реализована оригинальная, остроумная идея.
Остальные получают индивидуальные карточки с игрой «Судоку».
Блок 8 (резюме) обеспечивает обратную связь с учащимися на уроке и предусматривает качественную и эмоциональную оценку учащимся самого урока.
С помощью трёх смайликов (скучно, нейтрально, интересно) учащиеся показывают своё настроение в конце урока.
– Все этапы урока мы сегодня проводили в честь линейной функции. Поработали на славу. Но какой же бенефис без поэтической нотки.
– Поэтому в честь линейной функции мы заслушаем лучшее авторское стихотворение (заранее был объявлен творческий конкурс на лучшее стихотворение, посвященное линейной функции)
Линейной функции посвящается
Не знаю как вам,
А мне всё понятно-
Линейная функция неадекватна.
Она то прямой,
То отрезком бывает,
То ноль, то абсциссу
Одну пресекает.
Или вообще ординате равна-
На оси игрек она залегла.
Но в этом и прелесть,
Изюминка, соль:
Средь функций –
Линейный отрезок-король!
– Думаю, бенефис линейной функции удался.
– Т. к. сегодня вы очень старались и бенефис действительно получился, то домашнего задания не будет.
Ссылки на источники
- Жебровская О. О., к.п.н., доцент СПбГУ, «Международные сравнительные исследования PISA». Вебинар. http://s.ext.spb.ru/2_Webinars/2013-04-19-Webinar-16-30/PISA.pdf – [Дата обращения 10.07.2015].
- Концепция развития математического образования в Российской Федерации (утв. распоряжением Правительства РФ от 24 декабря 2013 г. N 2506-р)
- Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: Прикладной курс научного творчества: Учебное пособие. – Киров: АНОО «Межрегиональный ЦИТО», 2013. – 212 с.
- Альтшуллер Г. С., Верткин Н. М. «Как стать гением. Жизненная стратегия творческой личности!» – Минск, Беларусь, 1994 – 478 с.
