Развитие креативности школьников на уроках геометрии по системе НФТМ-ТРИЗ

Программа развития школы на 2011-2015 годы «Современное образование для развития успешной личности» ставит своей целью усовершенствовать школьную социокультурную образовательную среду для становления каждого учащегося как компетентной, социально интегрированной и мобильной личности, способной к саморазвитию, самореализации и самообразованию. Достижение обозначенного результата становится возможным благодаря формированию у учащихся познавательной активности, творческого мышления (креативного) и способности к самообразованию. В обучении профессиональному творчеству в нашей стране особое место занимает система НФТМ-ТРИЗ, которая основана на поисково-познавательной деятельности учащихся и направлена на развитие творческого воображения, используя свободу мыслеизъявлений.

Цель педагогической системы многоуровневого непрерывного креативного образования НФТМ-ТРИЗ: формирование личности учащегося, обладающей системным мышлением, способной решать творческие задачи любого уровня. Подцелями системы НФТМ - ТРИЗ являются формирование в учебном процессе, прежде всего, дивергентного мышления и воспитания креативных качеств личности. Конечной целью креативного образования является формирование высокодуховной, физически здоровой, творческой личности. Системе НФТМ –ТРИЗ присущи основные дидактические принципы, которые реализуются в учебном процессе через креативные инновационные педагогические технологии:

 принцип развития интеллектуальной активности личности, принцип непрерывности и преемственности творческого развития, принцип поисковой деятельности, принцип сотворчества, принцип обучения способам творческой деятельности и ускоренному приобретению опыта решения творческих задач, принцип положительного эмоционального фона, принцип предметной интеграции с методологией творчества ТРИЗ, принцип формирования системности мышления, принцип природосообразности принимаемых решений, принцип коммуникативности, принцип демократизации учебного процесса, принцип соревновательности, принцип развития смекалки («догадки») [3].

Целенаправленное развитие теоретического мышления учащихся следует сочетать с совершенствованием творческого мышления.

 Геометрия считается одним из самых сложных школьных предметов. Но именно при изучении этого раздела математики у учащихся формируются различные универсальные учебные действии, которые впоследствии способствуют развитию интеллектуальной активности личности, способной к поисковой и исследовательской деятельности, творческой самореализации, развитию творческого мышления со стандартизированной программой.

Чем выше уровень творческого развития ученика, тем выше уровень его общего умственного развития, тем выше его работоспособность. Именно поэтому одна из задач, которые ставит перед собой современный педагог – это развитие творческих способностей ученика. 

Тема урока: "Площади четырехугольников"

Место и роль урока в изучаемой теме: Данный урок является обобщающим в системе уроков по теме «Площадь», реально отражающий учебный план и оптимально соответствующий программе по учебнику Л. С. Атанасяна.

Тип урока: Повторительно-обобщающий.

Цель урока: Обобщение и систематизация знаний учащихся, формирование учебно-исследовательских навыков при решении практических задач (из "реальной математики") на вычисление площади фигур.

Учебные: проверить и систематизировать знания учащихся по данной теме; закрепить умения учащихся применять формулы нахождения площадей четырехугольников при решении практических задач; совершенствовать навыки решения задач на вычисление площадей различных многоугольников;

Развивающие: развивать у учащихся самостоятельность и способность к самоорганизации; совершенствовать умения логически и творчески мыслить и выражать свои мысли вслух; формировать навык исследовательской деятельности и повышать уровень математической культуры учащихся.

Воспитательные: воспитывать у учащихся стремление к совершенствованию своих знаний; воспитывать толерантность и умение работать в парах и группе.

 

Какова взаимосвязь темы урока с высказыванием ученого? сформулируйте самостоятельно цель урока (ответ учащихся). Да, действительно, мы посвятим урок решению задач на вычисление площадей плоских фигур. Посмотрим практическое применение нашей темы в реальном мире (попробуем себя в роли столяра, поставщика, паркетчика), а также будем работать с заданиями, которые включены в ОГЭ по математике.

Блок 2. Содержательная часть (метод контрольных вопросов)

а) Актуализация первичного субъективного опыта обучающихся (теоретический тест и самостоятельная работа с взаимопроверкой).

Начнем урок с повторения теоретического материала. Математическая разминка.

Для этого учащиеся отвечают на вопросы теста и заполняют таблицу. Работа проводится фронтально. Необходимо задействовать всех к разговору, к работе. Теоретический тест (листы у каждого ученика на парте, задания взяты с банка открытых заданий - подготовка к ГИА).
Теоретический тест.

1. Выберите верное утверждение:

a) Площадь прямоугольника равна произведению двух его сторон.

c) Площадь прямоугольника равна удвоенному произведению двух его соседних сторон.

2.Закончите фразу: Площадь ромба равна половине произведения…

a) его сторон.

b) его стороны и высоты, проведенной к этой стороне.

3. По формуле S = a· h_a можно вычислить площадь:

b) треугольника.

c) прямоугольника.

4. Площадь трапеции ABCD с основаниями AB и CD и высотой BH вычисляется по формуле…

a) S = AB: 2 · CD · DH.

b) S = (AB + BC) : 2 · BH.

5. Закончите фразу: Площадь прямоугольного треугольника равна:

a) половине произведения его стороны на какую-либо высоту.

c) произведению его стороны на проведенную к ней высоту.

6. По формуле S = ½ a ·h_a можно вычислить площадь:

a) параллелограмма.

b) квадрата.

7. Выберите верное утверждение:

a) Площадь прямоугольника равна произведению его сторон.

b) Площадь прямоугольника равна произведению его противоположных сторон.

 

1	2	3	4	5	6	7
b	c	a	c	b	c	c

Записать формулы площадей фигур (у каждого учащегося лист на котором фигуры с данными элементами). После взаимопроверки учащиеся сдают листы. Критерии оценок: нет ошибок - «5», 1 ошибка – «4», 2 ошибки – «3», более 2 ошибок - «2».

Если допущены ошибки, то на них остановиться, исправить, еще раз повторить формулы.

  

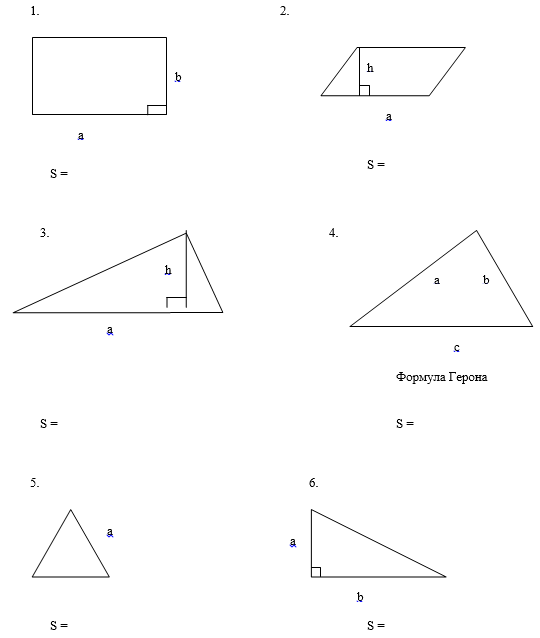
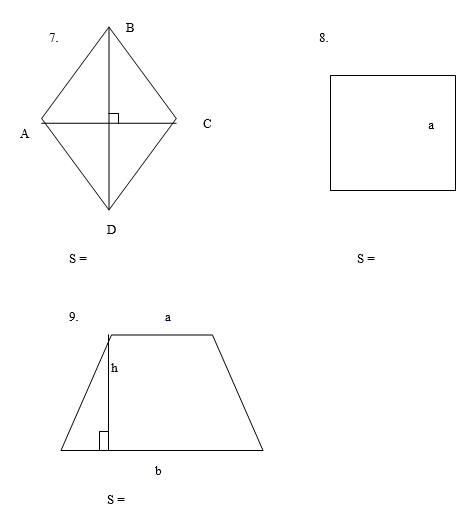
После выполнения работы ученики выполняют взаимопроверку. Критерий оценок.

(0 ошибок - «5», 1 ошибка – «4», 2 ошибки – «3»).

Если допущены ошибки, то на них остановиться, исправить, еще раз обговорить

в) Решение задач по теме (Прием усложняющихся задач)

1. В пря­мо­уголь­ни­ке одна сто­ро­на равна 96, а диа­го­наль равна 100. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

2) 

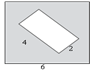
Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

3. Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 56. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции AECB.

4. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те пло­щадь тра­пе­ции.

5. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 30°. Най­ди­те пло­щадь ромба (задача с лишними данными).

6. Как найти же найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? (учащихся высказывают свои предложения по решению, самостоятельно делают вывод: разобьём эту фигуру на части - фигуры, площади которых, мы уже умеем находить)

 

а) "Историческая справка"

В каком году впервые упоминается о правилах измерения площадей? (сообщение предварительно подготовила ученица класса).

Первой из сохранившихся рукописей, в которых излагаются правила измерения площадей, была «Книга сошного письма», самый древний экземпляр, который относится к 1629 году, хотя имеются указания, что оригинал был составлен при Иване Грозном в 1556 году. В этой книге имеется глава «О земном верстании, как земля верстать». В ней, к сожалению, содержится много ошибочного материала в способах измерения площадей. Возможно, они появились в результате искажений во время переписывания от руки. Приходится признать, что уровень знаний был невысоким, хотя не хочется считать россиян шестнадцатого и семнадцатого столетий менее грамотными, чем древние египтяне. Тем более ярким подтверждением тому служат исключительные по красоте архитектурные памятники того времени, такие, как собор Василия Блаженного, построенный в 1553-1560 г.г. при Иване Грозном русскими «мастерами каменных дел Постником, Яковлевым и Бармой.

б)Физкультминутка.

Урок довольно сложен, отдых нам сейчас положен, Руки тянем выше, выше, Спинку держим, ровно дышим. Два наклона, поворот вправо и наоборот.

Мы минутку отдохнем и квадрат числа найдем.

Блок 4. "За страницами учебника". А знаете ли вы как определить площадь сложной фигуры, если она нарисована на клетчатой бумаге, и не вырождена - площадь ее ненулевая, все вершины имеют целые координаты, а стороны не пересекают друг друга – то удобно воспользоваться формулой Пика.

Если обозначить: В – количество целочисленных точек внутри этой фигуры, Г - количество целочисленных точек на ее границе, S – площадь фигуры, то

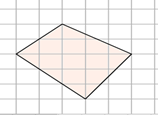
Рассмотрим следующую фигуру:

 

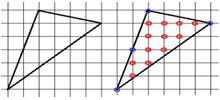
Обозначим все внутренние целочисленные точки красными кружками, а те, что на границах – синими. Целочисленные – это те, что лежат на пересечениях сетки (в ее узлах). Считаем те и другие: В=12, Г=4. Определим теперь площадь по формуле: S=В+Г/2-1=12+2-1=13. Давайте проверим правильность наших расчетов, тем более, что здесь это просто: рассчитаем площадь квадрата, обведенного красным цветом, и вычтем площади цветных треугольников:

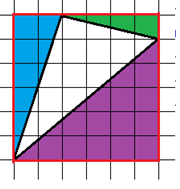Тогда площадь квадрата Sкв=36, площадь голубого треугольника 6, площадь зеленого – 2, площадь фиолетового 15.

Площадь белого треугольника тогда: S=36-6-15-2=13. Нравится ли вам этот способ нахождения площади фигуры? Определите (с вашей точки зрения) плюсы и минусы этого способа (ребята высказывают свое мнение).

Блок 4. "Мозговой штурм" (Деловая игра «Строитель»)

Цель игры: закрепить знания, умения и навыки при решении практических (нестандартных) задач с использованием формул площадей параллелограмма, трапеции, треугольника.

Основная идея игры состоит в том, чтобы создать производ­ственную ситуацию, в которой учащиеся, поставив себя на место человека той или иной специальности, смогут увидеть и оценить значение математических знаний в производительном труде, само­стоятельно овладеть необходимым теоретическим материалом и при­менить полученные знания на практике.

Строительное производство сегодня – это механизированный процесс сборки зданий и сооружений из крупноразмерных деталей, изготовленных заводским способом. Столяр работает на деревообрабатывающих предприятиях, в столярных мастерских. Работает на различных станках (круглопильных, фуговальных, шипорезных и т.д.) Непосредственно на строительном объекте столяр устанавливает оконные и дверные блоки, производит настилку дощатых и паркетных полов, монтирует встроенную мебель и т. д. Выполнение такой работы невозможно без знания устройства и правил эксплуатации деревообрабатывающих станков, умения читать чертежи. Профессия требует объемного воображения, хорошего глазомера, знания геометрии, рисования, черчения.

Сейчас, ребята, вы будете выступать в роли строителей. Требуется произвести настилку паркетного пола в игровом зале строящегося детского сада.

Размер пола 5,75 * 8 м. Паркетные плитки имеют форму прямоугольных треугольников, параллелограммов, равнобедренных трапеций. Размеры плиток даны в сантиметрах.

 

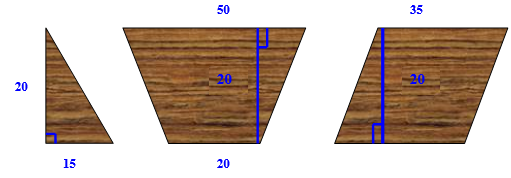
Правила игры.

Класс делится на три группы (бригады).

Первая – столяры. (Вам нужно изготовить плитки указанных размеров в таком количестве, чтобы после настилки пола не осталось лишних плиток и число треугольных плиток было минимальным, а плиток в форме параллелограммов и трапеций – одинаковое количество.)

Вторая – поставщики. (Вам нужно доставит необходимое количество плиток на строительную площадку. Значит, вам также нужно просчитать.)

Третья – паркетчики. (Чтобы проконтролировать доставку, надо наперед знать, сколько и каких паркетных плиток понадобится для покрытия пола.)

Паркет укладывается в ряды так, что параллелограммы и трапеции чередуются, а треугольников в одном ряду всего два.

Решение.

Подсчеты показывают, что в одном ряду по ширине укладываются по два треугольника и по восемь параллелограммов и трапеций.

1. Найдем площадь полоски шириной 20см и длиной 575см

S = 20 · 575 = 11 500см².

2. Найдем площадь одного треугольника

S = ½ · 15 · 20 = 150см².

3. Найдем площадь одного параллелограмма

S =35 · 20 = 700см².

4. Найдем площадь одной трапеции

S = ½ · (50 + 20) · 20 = 700см².

5. Найдем. Сколько в эту полоску вмещается параллелограммов и трапеций:

(11 500 – 2 · 150) : 700 = 16 . В полоску вмещается 8 параллелограммов и 8 трапеций.

6. Найдем, сколько таких полос в длине комнаты: 800: 20 = 40.

7. Найдем, сколько параллелограммов и трапеций в 40 полосках, т.е. во всей площади пола. Для этого 40 · 2 = 80.

Проверка:

1. Площадь всего пола:

S = 800 · 575 = 460 000см².

2. Воспользуемся свойством площадей

320 · 700 + 320 · 700 + 80 · 150 = 224 000 + 224 000+ 12 000 = 460 000см²

Задание данного уровня позволяют активизировать мыслительную деятельность учащихся, развивать логику и мышление, воспитывать интерес к предмету, учит анализировать, обобщать и рассуждать, а также способствует развитию творческих способностей. Используются принцип содружества, коммуникативности.

Вот и подошел к концу наш урок. Давайте подведем итоги. Мы повторили – …. Мы умеем – …Мы узнали новое - ....Сделаем выводы – ….Как высчитаете, актуальны ли в наше время слова Андрея Николаевича Колмогорова: «Знания по геометрии или умение пользоваться формулами необходимы почти каждому мастеру

или рабочему»? (заслушиваются ответы учащихся).

1) Повторить вопросы 1-10 (с.129-130), № 485, № 493

2) Дополнительно: Подсчитать какая сумма денег необходима для ремонта вашей комнаты (положить линолеум, поклеить обои). Данные для расчетов взять в магазине, Интернете, спросить у родителей и т.д.

 Приложение 1