Стратегия современного образования заключается в предоставлении возможности всем учащимся проявить свои таланты и творческий потенциал, подразумевающий возможность реализации личных планов. Эти позиции соответствуют современным гуманистическим тенденциям развития отечественной школы, для которой характерна ориентация педагогов на личностные возможности учащихся, их непрерывное «наращивание».
На сегодняшний день актуальна проблема поиска средств развития мыслительных способностей, связанных с творческой деятельностью школьников, как в коллективной, так и в индивидуальной форме обучения.
Одним из основополагающих принципов обновления содержания образования является его личностная ориентация, предполагающая опору на субъективный опыт учащихся, актуальные потребности каждого ученика. В связи с этим остро встал вопрос об организации активной познавательной и созидательной деятельности учащихся, способствующей накоплению творческого опыта школьников, как основы, без которой самореализация личности на следующих этапах непрерывного образования становится малоэффективной.
Под креативными способностями учащихся понимают то, что не сводится к знаниям, умениям и навыкам, а способность создавать, формулировать и разрабатывать необычные, оригинальные идеи, а также использовать нестандартные способы деятельности.
Основными показателями сформированности творческих способностей являются:
- Определенный фонд знаний и умений, их качество и степень обобщенности.
- Уровень развития: внимания, памяти, воображения.
- Уровень развития мышления, который определяется степенью сложности умственных действий и операций (анализ, синтез, сравнение, обобщение, классификация, конкретизация).
- Владение приемами поисковой и творческой деятельности.
Отследить показатели сформированности творческих способностей учащихся можно на уроках математики.
Задания креативного типа на уроках математики:
1) придумать обозначение числа, понятия;
2) дать определение изучаемому объекту, явлению;
3) сочинить задачу по схеме, математическую сказку;
4) сформулировать математическую закономерность;
5) составить кластер, математический кроссворд, игру, викторину, сборник своих задач;
6) изготовить модель, математическую фигуру, геометрический сад;
7) при работе в группах или парах по предложенным уравнениям, системам уравнений составить текст задачи и предложить их решить другим группам или парам;
8) создать презентацию, сайт, тест on-line по определённой теме, изученной или изучаемой.
Задания даются всему классу. При их выполнении оценивать следует только успех. Учащимся предлагался перечень задач, с помощью которых можно отследить развитие отдельных сторон умственных способностей на уроках. Эти задачи решались в процессе закрепления, как один из номеров проверочной или контрольной работ.
Инструментом для развития творческого мышления, творческого воображения, которые ведут к формированию творческой деятельности школьника, являются задачи «на соображение», «на догадку», головоломки, нестандартные задачи, логические задачи, творческие задачи. Их можно успешно использовать на уроках в качестве дополнительного пути для формирования элементов творческой деятельности.
Разработка урока по математике в 10-м классе по теме «Вычисление производных»
Цели урока:
- обобщить и оценить знания учащихся по данной теме;
- проверить умения учащихся применять формулы и правила вычисления производных;
- развивать мышление, речь, умение комментировать, тренировать память;
- воспитывать трудолюбие, чувство товарищества и взаимопомощи;
- прививать интерес к предмету путем дружеского соперничества в командах;
- формирование и дальнейшее развитие познавательных операций по планированию и прогнозированию учебной деятельности;
- развитие интеллектуальных умений и мыслительных операций − анализ и синтез, сравнение, обобщение;
- активизация мыслительной деятельности учащихся при решении задач прикладного характера, алгоритмизация деятельности.
Методы и приемы: словесный, наглядный.
По типу: урок обобщения и систематизации знаний.
Оборудование: раздаточный материал (разноуровневые карточки с практическими заданиями, листы учета знаний), плакаты с теоретическим материалом в схемах и таблицах, карточки с основными формулами.
Ход урока
1-й этап. Организационный момент
Эпиграфом к сегодняшнему уроку будут слова Ньютона «При изучении наук примеры не менее поучительны, нежели правила» и слова Ломоносова «Примеры учат больше, чем теория».
К этим словам мы вернемся позднее.
Класс разбивается на три разноуровневые группы (причем ребята сами оценивают свои знания и выбирают группу).
Капитан каждой группы получает памятку по оценки заданий и карточку с таблицей, в которую он будет выставлять баллы после каждого задания всем членам команды.
2-й этап. Комбинированная работа класса (работа у доски, работа по карточкам, устная и письменная работа с классом)
Разминка
- Представитель каждой команды вытягивает некоторую записанную букву алфавита.
- За три минуты придумать математические термины, начинающиеся на эту букву.
- За каждый названный термин команда получает один балл.
- Если группа сформулирует определение, то получает дополнительно еще три балла.
- Если группа не может сформулировать определение, то другие группы получают возможность заработать дополнительно три балла, сформулировав это определение.
Задача № 1
Расход горючего легкового автомобиля (литр на 100 км) в зависимости от скорости х км/ч при движении на четвертой передачи приблизительно описывается функцией f(x)=0,0017х2 - 0,18х + 10,2; х>30. При какой скорости расход горючего будет наименьший? Найдите этот расход.
Решение: Исследуем расход горючего с помощью производной: f'(х)=0,0034х-0,18.Тогда f'(х)=0 прих≈53. Определим знак второй производной в критической точке: f''(х)=0,0034>0, следовательно, расход горючего при скорости 53 км/ч будет наименьшим. f(53)≈5,43 л.
Задача № 2
Оборот предприятия за истекший год описывается через функцию U(t)=0,15t3 – 2t² + 200, где t – месяцы, U-миллионы. Исследуйте оборот предприятия.
Решение. Исследуем оборот предприятия с помощью производной:U'(t)=0,45t2 - 4t U''(t)=0,9t-4U'''(t)=0,9. Момент наименьшего оборота при U(t)=0, т.е.при t=8,9.Наименьший оборот был на девятом месяце. Первая производная показывает экстремальное изменение оборота. Из U(t)=0 следует t=4,4.Так как U'''(t)>0, то на пятом месяце имеется сильное снижение оборота.
Работа у доски (к доске вызываются трое учащихся):
Вычислить производную:
а) у = 4х2 + 5х + 8
б) у = (2х – 1)3 и найти их значение в точке х0 = 2.
Найти значения переменной х, при которых верно равенство:
а) sin' х = (х – 5)'
б) (2cos x)' = (х + 7)'
Вычислить производную: 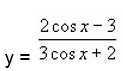
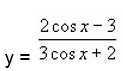
Работа по карточкам (разноуровневая работа, выполняется учащимися на местах):
Карточка № 1 (уровень А)
Найдите производную функции:
- у = 5 – 7х
- у = (х – 5)(2х – 5)
- у =
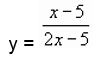
Карточка № 2 (уровень В)
Найдите производную функции:
- у = (х3 – 2х2 + 5)6;
- у = cos(х3-3)

Карточка № 4 (уровень А)
Найдите производную функции:
- у = cos x + ctg x
- y = 5 sin 3x
- y = 4x5 + tg 3x – cos2x
Устная работа с классом
Вычислить производную:
- у = 2х – 3
- у = х2 – 3х + 4
- у = 3 cosx
- у = sin5x
- у = tg(2 – 5х)
- у = arcsin2х
- у = (х – 3)2
- у = (3 – 4х)2
9. Дана функция f(x) = 4х2. Вычислить f '(1), f '(-2).
10. Дана функция f(x) = х3. Решите уравнение: f(x) = f '(х).
Письменная работа с классом
Решить уравнение: ((41 – 5х)2)' = х0, где х0 – корень уравнения 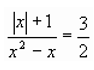 .
.
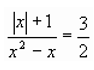 .
.3-й этап. Работа по группам
Каждая команда получает карточки с заданиями разного уровня сложности.
По одному человеку от команды решают у доски, остальные в тетрадях.
Карточка № 1 (уровень сложности А)
Найдите производную функции:
- у = 4х4 - х5 + х2 -3х
- у = (х + 4)3 у =
- Вычислите у '
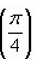 , если у(х) = ctgx – tgx.
, если у(х) = ctgx – tgx. - Решите уравнение: f ' (x) = 0, если f (x) = х4 - 2х2 + 1
Карточка № 2 (уровень сложности В)
Найдите производную функции:
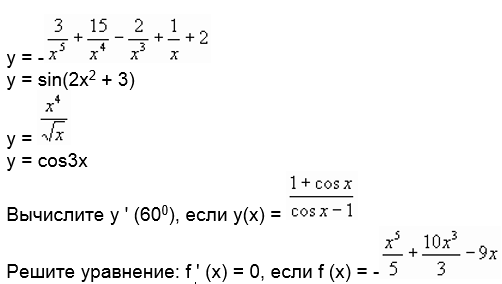
Дополнительно. Решить уравнение | х + 2 | + | х – 3 | = 5
Карточка № 3 (уровень сложности С)
Найдите производную функции:
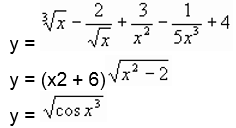
4) у = arctg 2x
5) Вычислите у ' , если у(х) = sin x · cos2 x
6) Решите уравнение: f ' (x) = 0, если f (x) = x – tg x
7) Дополнительно. Решить неравенство у ' > 0, если у(х) = (3х – 1)10 · (2х + 5)7.
4-й этап. Соревнование по группам
На доске записаны задания трех уровней сложности. Каждая группа выбирает свой уровень и выполняет задания в группе на местах, распределяя задания на каждого ученика группы. Каждому заданию соответствует некоторая буква. На полученное слово составить несколько предложений.
Выигрывает та команда, которая вперед угадывает слово.
Вычислить производную:


Шифры:


Задания, с которыми не справились группы, решаются совместно, обосновываются выводы.
Капитан оценивает работу каждого по следующим критериям:
- решил сам без ошибок и помог товарищу – 5 баллов
- решил сам, но консультировался у товарища – 4 балла
- решал с помощью карточки с формулами и учителя – 3 балла
Предлагается творческое задание (при наличии времени на уроке, если имеем в наличии сдвоенные уроки. Если такая возможность отсутствует, творческое задание выполняется дома).
Задача № 3
За последние 10 лет численность грызунов в городе Н выросла в 5 раз и достигла 1 миллиона особей: по одной крысе на каждого жителя. За год одна пара крыс способна воспроизвести 50 штук себе подобных. По словам эпидемиологов, крысы являются переносчиками многих болезней – чумы, бешенства, энцефалита. Составьте задачу по приведенным данным и решите её.
Задача № 4
Зависимость суточного удой У в литрах от возраста коров Х в годах определяется уравнением У(х)= -9,3+6,86х-0,49х , где х>2.Найдите возраст дойных коров, при котором суточный удой будет наибольшим.
5-й этап. Итог урока
1) Самооценка труда учащихся:
- Выполнил ли программу урока полностью;
- Какие виды работ вызвали затруднения и требуют повторения;
- В каких знаниях уверен.
2) Оценка труда товарищей:
- Кто, по вашему мнению, внес наибольший вклад;
- Кому, над чем следовало бы еще поработать.
3) Оценка работы класса учителем
6-й этап. Домашнее задание: составить проверочную карточку из трех заданий по данной теме (разноуровневую).
Ссылки на источники
- Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: Прикладной курс научного творчества: Учебное пособие. – Киров: АНОО «Межрегиональный ЦИТО», 2013. – 212 с.
- Михайлов В.А., Горев П.М., Утёмов В. В. Научное творчество: методы конструирования новых идей: Учебное пособие. – Киров: ЦИТО, 2014. – 80 с.
- Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. Просвещение, 1990.
