Развитие креативных способностей учащихся на уроках математики

Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности. Велика роль задач в развитии мышления и в математическом воспитании учащихся, в формировании у них умений и навыков в практических применениях математики.

Обобщающий урок представляет собой разработку спаренных уроков по алгебре в 9-м классе по теме «Решение текстовых задач». Данные уроки могут быть проведены как с целью повторения решения текстовых задач по всему курсу основной средней школы, так и для подготовки обучающихся к сдаче экзаменов в 9-х классах при тематическом повторении. 

Цели урока:

дидактические:

- повторение, обобщение, систематизация знаний;

- проверка уровня усвоения темы;

- развитие у учащихся интереса к предмету через решение прикладных задач и умения применить математические знания в практической деятельности.

психологические:

- формирование и дальнейшее развитие познавательных операций по планированию и прогнозированию учебной деятельности;

воспитательные:

- формирование логического, системного мышления;

- развитие интеллектуальных умений и мыслительных операций − анализ и синтез, сравнение, обобщение.

Тип урока: обобщение и систематизация знаний.

Оборудование: компьютер, мультимедийный проектор, интерактивная доска.

На сегодняшнем уроке мы продолжим разговор о текстовых задачах.

Задача 1. В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Узнать число фазанов и число кроликов. Кто хочет поразмыслить по поводу этой задачи? Ведь это всем известная задача.

Задача 2. Мама раздала детям по четыре конфеты, и три конфеты остались лишними. А чтобы дать детям по пять конфет, двух конфет не хватает. Сколько было детей?

Кто хочет поразмыслить по поводу этой задачи?

Задача 3. Может ли такое быть? Одного человека спросили:

- Сколько вам лет?

- Порядочно, – ответил он.

- Я старше некоторых своих родственников почти в шестьсот раз. Может ли такое быть? Может, например если человеку 50 лет, а его внуку или внучке 1 месяц.

Ответьте на вопросы:

- Какую формулу следует применить при решении задач на движение? Что в данной формуле обозначают буквы S, t, v?

- Какие величины используют при решении задач на работу? Как можно задать формулу работы?

- Что такое производительность труда и можно ли ее сравнить со скоростью движения?

Уравнения, которые составляются на основании условий задач на движение, обычно содержат такие величины, как расстояние, скорости движущихся объектов, время, а также скорость течения воды (при движении по реке).

Задача 1. Пароход прошел 4 км против течения реки, а затем прошел еще 33 км по течению, затратив на весь путь один час. Найдите собственную скорость парохода, если скорость течения реки равна 6,5 км/ч [2].

Пусть х км/ч – собственная скорость парохода.

Тогда  (х+6,5) км/ч – скорость парохода по течению.

(х–6,5) км/ч – скорость парохода против течения.

Так как против течения пароход прошел 4 км со скоростью (х–6,5) км/ч, то

ч – время движения парохода против течения.

Так как по течению пароход прошел 33 км со скоростью (х+6,5) км/ч, то

ч – время движения парохода по течению.

По условию

решим полученное уравнение 

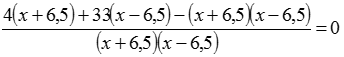
Откуда получаем квадратное уравнение

х²–37х+146,25=0 Þх₁=4,5 км/ч и х₂=32,5 км/ч.

Осуществим отбор полученных решений.

Через х мы обозначили собственную скорость парохода, при этом скорость течения реки 6,5 км/ч, поэтому х₁=4,5 км/ч не подходит по смыслу задачи (при такой скорости пароход не выплыл бы против течения). Поэтому, собственная скорость парохода равна 32,5 км/ч. Ответ: v=32,5 км/ч.

Задача 2. В заезде на одну и ту же дистанцию участвовали два автомобиля и мотоцикл. Второму автомобилю на всю дистанцию потребовалось на 1 мин больше, чем первому. Первый автомобиль двигался в 4 раза быстрее мотоцикла. Какую часть дистанции в минуту проходил второй автомобиль, если он проходил в минуту на 1/6 дистанции больше, чем мотоцикл, а мотоцикл прошел дистанцию меньше, чем за 10 мин? [2]

 

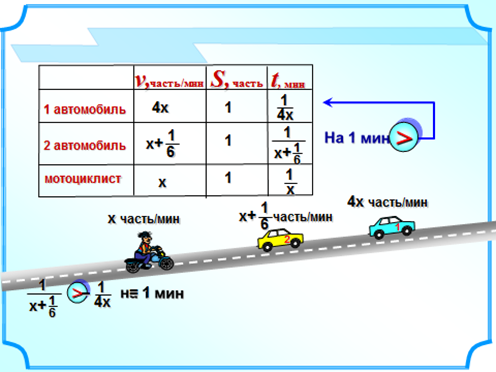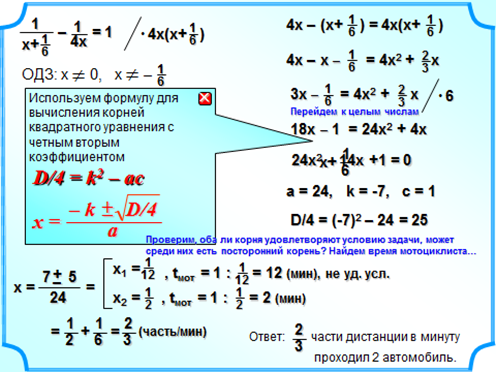Рис. 1. Условие задачи	Рис. 2. Решение задачи

 

Работа в ППС (пары постоянного состава)

Через мультимедийный проектор выведены на экран тексты задач с вариантами ответов и предложено ученикам выбрать верный. Выбор обосновать.

1. Из пункта А в пункт В одновременно выехали два попутчика, один со скоростью 25 км в час, а второй 40 км в час. Если тот, который движется быстрей, прибыл на 3 часа раньше другого, то найдите расстояние между городами.

А)150        В)180             С)200          Д)220           Е)250

2. Пешеход должен был пройти 9 км с некоторой скоростью, но увеличив эту скорость на 2 км в час, он прошел 9 км на 45 мин быстрее. Найдите истинную скорость пешехода.

А) 3            В) 5                 С) 4              Д) 6              Е) 2

3. Теплоход прошел 4 км против течения реки и затем прошел еще 33 км по течению, затратив на весь путь 1 ч. Найдите скорость теплохода в стоячей воде, если скорость течения реки равна 6,5 км в час.

А) 33         В) 40              С) 31            Д) 32,5         Е) 25

Активируем «Кнопки мозга» – выполняется стоя или сидя. Для начала мысленно проведем линию ото лба к носу, подбородку и ниже – она разделяет тело на правую и левую половины. Движения, пересекающие эту линию, интегрируют работу полушарий мозга. Поэтому «Перекрестные шаги» способствуют развитию координации и ориентации в пространстве, делают более успешными приобретение навыков чтения, письма, слушания, усвоения новой информации. А еще снимают боль в пояснице и подтягивают мышцы живота.

- Ноги стоят удобно, параллельно друг другу. Если вы стоите, то колени расслаблены. Одна рука кладется на пупок. Пальцы другой руки прикасаются к двум точкам, расположенным под ключицами между первым и вторым ребром, таким образом, что большой палец оказывается на одной точке, а средний – на другой.

- Далее слегка массируем эти точки пальцами. Рука на пупке просто спокойно лежит.

- Меняем руки и повторяем упражнение, по 30Х30 секунд.

- Выполнение упражнения «Кнопки мозга» способствует обогащению мозга кислородом, за счет этого улучшается восприятие информации.

4.  Головоломки. Математические ребусы

Ответы: Ребус 1.Задача, ребус 2. цифра, ребус 3. математика.

Старайтесь решать задачи красиво, без лишних выкладок и перебора случаев. Для математика важна не сумма методов решения задач, но, прежде всего, математическая интуиция, которая ведет к цели. Давид Гильберт говорил, что тот, кто может решить следующую задачу в уме без вычислений, – тот прирождённый математик [3, 4].

Пример. Из чашки с кофе в чашку с молоком перелили ложку кофе, затем такую же ложку смеси перелили обратно. Чего больше: молока в чашке с кофе или кофе в чашке с молоком?

Решение. Попробуем угадать ответ. Для этого рассмотрим крайний случай (это первая идея). Пусть в чашках налито по одной ложке, тогда заберем весь кофе и получим равномерную смесь. Кофе и молока будет поровну. Всегда ли будет поровну? Поскольку перелили «туда» и обратно одну ложку, то (вторая идея) объем жидкости в чашках не изменился. Следовательно, (третья идея) сколько кофе убыло – столько молока прибыло.

Замечание. Объёмы кофе и молока в чашках могут быть неравными, можно переливать ложку туда и обратно хоть десять раз, можно плохо размешивать перелитую ложку все равно молока в кофе будет столько же, сколько кофе в молоке! [3].

Содержание задач этого типа сводится обычно к следующему: некоторую работу, объем которой не указывается и не является искомым, выполняют несколько человек или механизмов, работающих равномерно, то есть с постоянной для каждого из них производительностью. В таких задачах объем всей работы, которая должна быть выполнена, принимается за 1; время t, требующееся для выполнения всей работы, и р – производительность труда, то есть объем работы, сделанной за единицу времени, связаны соотношением

Задача. Двое рабочих выполняют некоторую работу. После 45 минут совместной работы первый рабочий был переведен на другую работу, и второй рабочий закончил оставшуюся часть работы за 2 часа 15 минут. За какое время мог бы выполнить работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 час больше, чем первому [2].

Пусть х – время работы первого по выполнению всей работы.

у – время работы второго рабочего.

По условию х=у–1, и первое уравнение составлено.

Пусть объем всей работы равен 1.

Тогда  – производительность труда первого рабочего,

– производительность труда второго рабочего.

Так как они работали 45 мин.=3/4 часа совместно, то

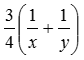– объем работы, выполненной рабочими за 45 минут.

Так как второй рабочий работал один 2 часа 15 минут=2¼=9/4 часа, то

– объем работы, выполненной вторым рабочим за 2 часа 15 минут.

По условию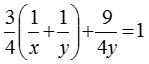          

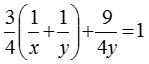
Таким образом, мы получили систему двух уравнений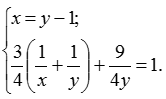 

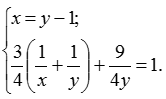
Решим ее, для этого выражение для х из первого уравнения подставим во второе

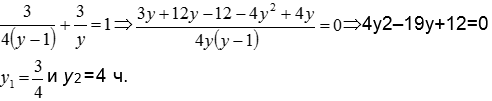
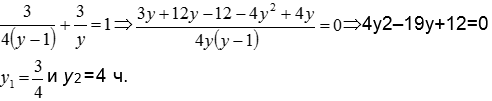
Из двух значений для у выберем то, которое подходит по смыслу задачи у₁ = 45 мин, но 45 мин рабочие работали вместе, а потом второй рабочий работал еще отдельно, поэтому  не подходит по смыслу задачи. Для полученного у у₂=4 ч найдем из первого уравнения первоначальной системы значение х

х=4–1 Þ х=3 ч.

Ответ: первый рабочий выполнит работу за 3 часа, второй – за 4 часа.

Замечание: эту задачу можно было решить, не вводя вторую переменную у, а выразить время работы второго рабочего через х, тогда нужно было составить одно уравнение и решить его.

Решение задач (первые две задачи ученики решают на доске с подробными комментариями и грамотным оформлением; третью задачу – самостоятельно в тетради с обязательной устной проверкой составленного уравнения и ответа).

Распечатанные тексты заданий разложены на партах.

Учащимся даётся индивидуальная карточка, в которой нужно ответить на вопросы:

- Какой этап урока тебе был самым интересным в познавательном плане?

- На каком этапе ты почувствовал эмоциональный подъём?

- Какой этап урока тебе показался скучным?

- Поставь оценку работе всего класса за работу на уроке, можно с комментариями.

Великий китайский мудрец Конфуций (около 551-479 лет до н. э.) две с половиной тысячи лет назад сказал: «Когда благородный муж учит и воспитывает, он ведет, но не тянет за собой, побуждает, но не заставляет, указывает путь, но позволяет ученику идти самому. Поскольку он ведет, а не тянет, он пребывает в согласии с учеником. Поскольку он побуждает, а не заставляет, учеба дается ученикам легко. Поскольку он лишь только открывает путь, он предоставляет ученику возможность размышлять». Такая позиция очень близка современному учителю и современным детям.