В современной школе математика является одним из значимых предметов с точки зрения её вклада в развитие интеллекта учащихся. Школьное математическое образование развивает воображение и интуицию, формирует навыки логического и алгоритмического мышления. Благодаря своей универсальности математика вооружает учащихся методами познания других наук. При этом знания по математике у школьников не всегда отвечают требованиям к планируемым результатам обучения. Как показывает практика, даже высокие результаты обучения математике учащихся не дают гарантии, что государство в дальнейшем получит высококвалифицированных специалистов, способных применить свои математические способности для решения практических задач. Школа пока ещё продолжает ориентироваться на обучение, выпуская в жизнь человека обученного – квалифицированного исполнителя. Однако, современному обществу необходим обучаемый человек, способный самостоятельно учиться и многократно менять спектр своих действий и умений в течение жизни, готовый к активным и целесообразным самостоятельным действиям и принятию ответственных решений.
Вот почему в настоящее время проблема самостоятельного успешного усвоения учащимися новых знаний, умений и компетенций, включая умение учиться, приоритетна.
Работ, посвященных проблеме формирования УУД при обучении математике в основной школе, не так много (А.Г. Асмолова, Л.И. Боженковой, И.Г. Липатниковой). Их важной особенностью является то, что в них предлагается конкретный материал и рекомендации по формированию отдельных видов УУД [3, 6, 1, 5].
Образование в 5-6 классах школы является фундаментом всего последующего обучения, так как закладывает основу формирования учебной деятельности учащихся – систему учебных и познавательных мотивов, умение принимать, сохранять, реализовывать учебные цели, умение планировать, контролировать и оценивать учебные действия и их результат.
Курс математики 5-6 классов на современном этапе призван решить следующие задачи:
- обеспечить прочное и сознательное овладение системой математических знаний и умений, необходимых для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
- обеспечить интеллектуальное развитие, сформировать качества мышления, характерные для математической деятельности и необходимые для полноценной жизни в обществе;
- сформировать умение учиться;
- сформировать представление об идеях и методах математики, о математике как форме описания и методе познания окружающего мира;
- сформировать представление о математике, понимание значимости математики для общественного прогресса;
- сформировать устойчивый интерес к математике;
- выявить и развить математические и творческие способности.
Решение данных задач определяет требования, сформулированные в ФГОС второго поколения, и обеспечивается, прежде всего, через формирование УУД, которые являются инвариантной основой образовательного и воспитательного процесса.
Рассмотрим приемы формирования каждой группы УУД на уроках математики в основной школе (5-6 классы).
Регулятивные УУД.
1. В соответствии с теорией П.Я. Гальперина необходимо организовать работу учащихся таким образом, чтобы учитель имел возможность проконтролировать ход выполнения каждой операции и результаты её выполнения. Для этого в условия составленных заданий учителю необходимо закладывать письменные дополнительные вопросы. При помощи последовательности верных ответов на
данные вопросы учащийся самостоятельно может приходить к верному решению, формулируя новые понятия, алгоритмы, правила и пр. Таким образом, при разбиении задания на подзадания ученик учится планировать свою деятельность, может видеть, как одно правило вытекает из другого.
Пример задания 5-6 класса по теме «Взаимно обратные числа», [4, с. 57].
|
|
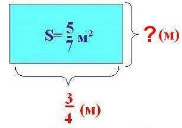
Площадь прямоугольника 5/7 кв.м. Длина одной стороны ¾ м. Найдите длину другой стороны? |
Письменно ответьте на вопросы и заполните пропуски:
1) Запишите формулу для вычисления площади прямоугольника со сторонами а и b: S=
2) Чему равна площадь данного прямоугольника?
3) Чему равна длина одной стороны?
4) Зная площадь и длину одной из сторон, как найти длину второй стороны?
5) Какое арифметическое действие необходимо проделать, чтобы найти длину второй?
6)Умеем ли мы выполнять это действие с дробями?
Каким компонентом деления является 5/7 ?
Каким компонентом деления является ¾ ?
7) В результате данного действия получится длина второй стороны прямоугольника. Обозначим ее какой-нибудь переменной. Например, х.
Запишите полученное уравнение:
Каким компонентом деления является х?
8) Умеем ли мы выполнять данное действие с обыкновенными дробями?
9) Выразите 5/7 из имеющегося уравнения:
Получим уравнение вида:
10) Вспомним, какие числа называются взаимно обратными?
Взаимно обратные числа – это числа, …
11) Число взаимно обратное числу ¾ это число: .
12) Можно ли домножить левую и правую часть полученного уравнения на число взаимно обратное __?
13) Измениться ли после этого корень уравнения?
Решим задание, заполнив пропуски:
Таким образом, при разбиении многошагового задания на подзадания ученик учится планировать свою деятельность, может видеть, как одно правило вытекает из другого.
2. Задание на нахождение дроби от числа с использованием понятия «проценты» по математике для учащихся 5-6 классов [4, с. 27].
Огород занимает 8 га.
Картофелем занято 45% площади этого огорода.
Сколько гектаров занято картофелем?
Перед решением задания, ответьте письменно на следующие вопросы:
1) Что такое 1%?
2) Как перевести проценты в дробь (десятичную дробь)?
3) Сколько гектаров занимает весь огород?
4) Сколько процентов площади этого огорода занято картофелем?
5) Можно ли представить 45% в виде десятичной или обыкновенной дроби?
6) Запишите 45% в виде десятичной дроби: 45% =
7) Какую часть от всего огорода занимает картофель?
8) К какому типу заданий можно отнести данное задание?
9) Как найти дробь от числа?
Данное задание предлагается учащимся до изучения вопроса «решение задач на нахождение процента от числа».
Принимая участие в разборе заданий, содержащих дополнительные вопросы, понимая сущность и значение дополнительных вопросов для решения математических задач, в дальнейшем ученик сам может составлять дополнительные вопросы к любому заданию из учебника.
При правильном составлении учащимся дополнительных вопросов к математической задаче или заданию, у него формируются регулятивные УУД.
Личностные УУД.
1. Важным этапом при системе обучения, предложенной П.Я. Гальпериным,
является выполнение реальных действий в материальном или материализованном виде. В качестве таких объектов выступают чертежи, схемы, рисунки, диаграммы, макеты, модели, таблицы и просто записи, которые позволяют понять ситуацию,
«увидеть» происходящие изменения, описанные в условии, удерживать в памяти известные в задании данные в процессе его решения.
Рассмотрим пример задания 5-6 класса на нахождение дроби от числа [4].
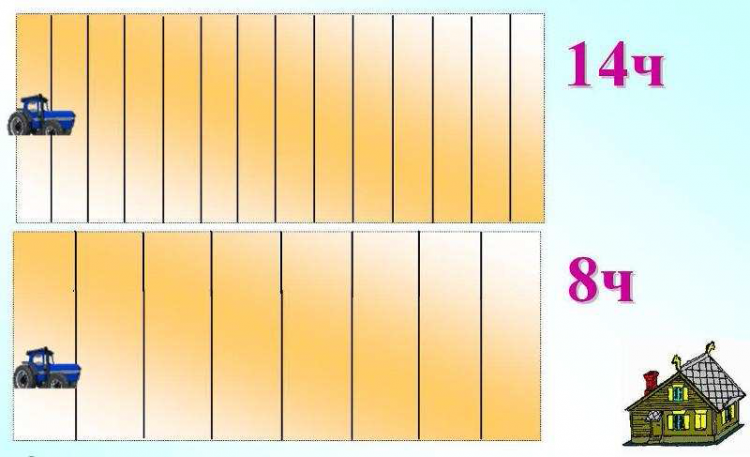
Один трактор может вспахать поле за 14 часов, а другой за 8 часов.
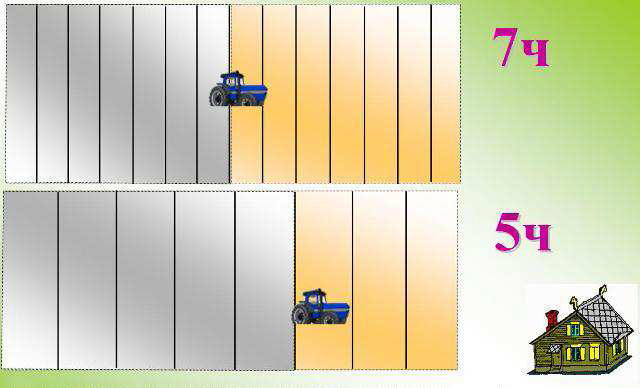
Какой трактор вспашет большую часть поля: «Первый за 7 часов, или второй за 5 часов»?
1) За сколько часов может вспахать поле первый трактор?
2) За сколько часов может вспахать поле второй трактор?
3) Какой трактор быстрее вспашет всё поле?
Решение подобных заданий способствует появлению интереса у учащихся.
Изучая рисунок и отвечая на поставленные вопросы, ученик видит значимость данного задания и увязывает его с реальными жизненными ситуациями (вспашка поля).
2. В ходе решения заданий, связывающих математику с действительностью, учащиеся самостоятельно или при помощи учителя устанавливают связь между целью учебной деятельности и ее мотивом. При этом они видят смысл производимых действий и могут осознать необходимость изучения представленной информации в дальнейшем. В результате проделанных действий у учащихся постепенно формируются личностные УУД.
Пример задания 5-6 класса на применение правила умножения дроби на натуральное число.
Шаг папы равен 4/5 метра. Обычно он совершает 60 шагов в минуту.
Шаг его сына равен 3/5 метра. В одну минуту он совершает 35 шагов.
Чтобы встретить сына из школы папе потребовалось 7 минут для прохождения пути от дома до школы.
На обратный путь у папы вместе с сыном ушло в два раза больше времени, при этом сын пришёл домой мокрый и уставший. Сколько времени потратил бы сын на дорогу от школы до дома, если бы шел один? Как Вы думаете, почему он пришел в таком состоянии из школы?
Данное задание показывает, что необходимо пользоваться общими правилами поведения для всех людей при решении любой проблемы.
В ходе его решения, учащиеся самостоятельно или при помощи учителя устанавливают связь между целью учебной деятельности и ее мотивом, а также видят смысл проводимых действий, которые их мотивируют к необходимости изучения данного математического правила для использования его в реальной жизни.
Познавательные УУД.
1. Формирование познавательных УУД возможно при выделении необходимой информации из представленных данных, при соотнесении известной и неизвестной информации, а также при структурировании знаний от того, что имеем для того, что нужно найти.
Пример задания 5-6 класса на умножение обыкновенных дробей [4, с. 9].
Ответьте письменно на вопросы:
1) Рассмотрим выражение 1 2/7 ×1 ¾. Произведение, каких чисел дано?
2) Перечислите порядок действий, который необходимо проделать, для того чтобы выполнить умножение и получить верный ответ:
3) Какое число получится при перемножении числителя одной неправильной дроби на числитель другой?
4) Какое число получится при перемножении знаменателя одной неправильной дроби на знаменатель другой?
5) Нужно ли выполнить сокращение полученного ответа или получилась несократимая дробь;
6) При перемножении одной неправильной дроби на другую, какая дробь в результате получилась - правильная или неправильная?
7) Что необходимо сделать с полученной дробью, чтобы записать конечный ответ?
Выполните умножение: (даются примеры).
При выполнении задания учащимся необходимо сначала ответить на письменные дополнительные вопросы, а затем выполнить умножение.
Ответ на первый дополнительный вопрос способствует тому, чтобы учащиеся извлекали информацию из условия задания, используя имеющиеся знания.
Далее учащимся необходимо перевести смешанные дроби в неправильные
и, используя правило умножения дроби на дробь, перемножить числители с
числителями, знаменатели со знаменателями. При этом учащимся необходимо
выбрать эффективный способ решения. Выполняя эти действия, они должны
увидеть, что удобнее сначала сократить дробь, а потом перемножить
оставшиеся множители. Следовательно, данное задание ориентировано на
формирование познавательных УУД.
2. Пример задания 5-6 класса по теме: «Применение распределительногосвойства умножения» из разработанной рабочей тетради [4, с. 39].
 |
Чтобы сшить платье Юле необходимо 4 2/3 метра ткани. Сколько метров ткани нужно Юле чтобы сшить 3 таких же платьев? |
Перед решением ответьте письменно на вопросы:
1) Вы когда-нибудь шили сами платье?
2) Нравиться ли Вам шить?
3) Сколько метров ткани необходимо Юле чтобы сшить одно платье?
4) Что просят найти в задаче?
5) Что для этого нужно сделать?
6) Запишите 4 2/3 в виде суммы двух слагаемых (целой и дробной части):
7) Сколько платьев необходимо сшить по условию задачи?
8) Запишите произведение суммы двух чисел 4 и 2/3 и натурального числа 3:
9) Как называется свойство, которым необходимо воспользоваться далее при вычислении?
10) Произведите вычисление умножения, используя данное свойство:
11) Можно ли решить данную задачу, не используя распределительное свойство умножения относительно сложения?
12) Что необходимо сделать со смешанным числом при умножении его на целое число?
13) Представьте смешанное число 4 2/3 в виде неправильной дроби:
14) Произведите вычисление умножения полученной неправильной дроби на натуральное число?
15) Какой способ выполнения задания Вам показался легче и быстрее?
Поставлена задача вычислить необходимый метраж ткани на платье с использованием распределительного свойства умножения относительно сложения. Данное задание сначала представлено без вспомогательных вопросов, для того чтобы учащийся обратил внимание на его схожесть со стандартными заданиями из учебника и смог сам проанализировать его условие про себя. Задание изначально представлено совместно с иллюстрацией, что дает визуальную информацию о ситуации. Вопросы побуждают учащихся найти необходимую информацию в условии задания и проанализировать её. При выполнении данных действий в ходе ответа на поставленные вопросы у учащихся формируются познавательные УУД.
Коммуникативные УУД.
Развитие коммуникативных умений: устная научная речь и развитие комплекса умений, на которых базируется грамотное эффективное взаимодействие.
1. К первому направлению можно отнести все задания, сопровождающиеся
инструкциями «Расскажи», «Объясни», «Обоснуй свой ответ», и все задания,
обозначенные вопросительным знаком.
2. Ко второму направлению формированию коммуникативных универсальных учебных действий относится система заданий, нацеленных на организацию общения учеников в паре или группе (все задания, относящиеся к этапу первичного применения знаний; к работе над текстовой задачей, осуществляемой методом мозгового штурма и т.д.)
Основой развития коммуникативных умений может служить систематическое использование на уроках трех видов диалога:
а) диалог в большой группе (учитель – ученики);
б) диалог в небольшой группе (ученик – ученики);
в) диалог в паре (ученик – ученик).
1. Блоки заданий по темам (прием основан на технологии коллективного способа обучения КСО, описанного в трудах Виталия Кузьмича Дьяченко, который наиболее ярко способствует формированию коммуникативных УУД).
1. Учитель заготавливает карточки с заданиями (карточки могут быть разных уровней сложности). Карточек делается столько, сколько учеников в классе. Количество заданий в одной карточке от 1 до 3. Так, например, один блок карточек состоит из задач повышенной сложности, другой – из задач средней сложности, третий блок включает простые задачи.
Все ученики разбиваются внутри блока парами. Один ученик объясняет решение первой задачи своему партнёру. Второй слушает, осмысливает, задаёт вопросы, то есть контролирует и проверяет работу своего партнёра, затем они меняются ролями.
2. Каждый ученик решает первую задачу из карточки соседа самостоятельно.
3. Учащиеся берут друг у друга тетради и проверяют правильность решения задач. Если они неправильные, то идёт повторное объяснение.
4. После работы над первой задачей из карточки соседа каждый ученик самостоятельно решает вторую задачу.
5. После решения задач ученики обмениваются тетрадями и проверяют их. Если решение неправильное, то идёт объяснение второй задачи. Этот этап длится до полного усвоения решения задач. Ученики оценивают работу друг друга, подводятся итоги.
2. Дидактическая игра «Зажги салют».
Тема: Проценты. Решение задач на проценты (5 класс).
Эта игра также заставляет школьников активно участвовать в выполнении предложенных заданий, работая в группе (команде).
Каждый ряд - это команда. Команде вручается конверт с карточками; на первой парте раскладываются "звезды" произвольной формы (из цветной бумаги), на обратной стороне которых написаны ответы. На доске нарисованы 3 "куста" с "ветками" по количеству карточек. Команда, решив задачу, ищет "звезду" с ответом и прикрепляет её на "ветки" с помощью магнита.
Выигрывает та команда, которая первая "зажжет салют".
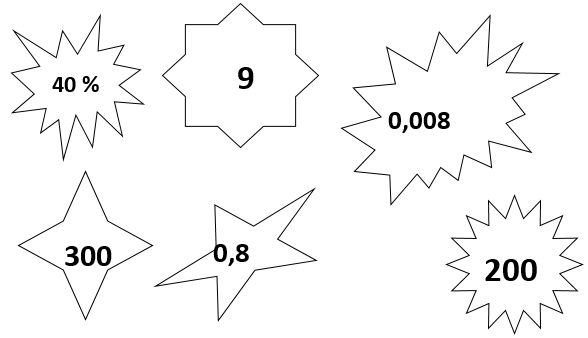
Карточки с заданиями.
- Выразите в процентах число ноль целых четыре десятых.
- Представьте в виде десятичной дроби ноль целых восемь десятых процента.
- Найдите три процента от трехсот.
- Найдите число, тридцать процентов которого равны девяноста.
- Найдите восемь процентов от единицы.
- Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества, сколько насосов высшей категории качества изготовило предприятие?
Ссылки на источники:
1. Боженкова, Л. И. Методика формирования универсальных учебных действий при обучении геометрии [Текст] / Л. И. Боженкова. – М. :ИНОМ. Лаб. знаний, 2013. – 205 с. : ил.
2. 15. Гальперин, П. Я. Основные результаты исследования по проблеме «Формирование умственных действий и понятий» [Текст] /П. Я. Гальперин. – М. : Изд-во МГУ, 1965. – 51 с.
3. Как проектировать универсальные учебные действия в начальной школе. От действия к мысли [Текст]: пособие для учителя / А. Г. Асмолов, Г. В. Бурменская, И. А. Володарская [и др.]; под ред. А. Г. Асмолова. – 2-е изд. – М. : Просвещение, 2010. – 152 с. : ил.
4. Квитко, Е. С. Умножение обыкновенных дробей [Текст]: рабочая тетрадь по математике для 5-6 класса / Е. С. Квитко. – М.: Аттика - центр, 2012. – 64 с.
5. Липатникова, И. Г. Рефлексивный подход к обучению математике учащихся начальной и основной школы в контексте развивающего обучения [Текст] : дисс. … канд. пед. наук : 13.00.02 / И. Г. Липатникова ; ГОУ ВПО «Уральский гос. пед. ун-т» ; науч. конс. : В. А. Далингер. – Екатеринбург, 2005 – 395 с.
6. Формирование универсальных учебных действий в основной школе. Система заданий [Текст]: пособие для учителя / А. Г. Асмолов,Г. В. Бурменская, И. А. Володарская [и др.]; под ред. А. Г. Асмолова. – 2-е изд. – М. : Просвещение, 2011. – 159с. : ил. – (Стандарты второго поколения).