Важной особенностью информационной цивилизации состоит в том, что возрастает роль человека. Человек является движущим фактором в развитии общества. Мы живём в мире, наполненном информацией. Поэтому процесс обучения и образования необходимо направить на умение ребенка принятия правильных решений в выборе информации, ее осмысления, внедрения в жизнь. Учащийся должен уметь обрабатывать новую информацию, опираясь на свой опыт. Меняются способы работы с информацией. Все чаще используются компьютерные технологии. Все это требует совершенствования образовательного процесса. Как никогда ранее важно уметь составлять и использовать алгоритмы для решения различных задач. Именно уроки математики способствуют формированию умения формальным языком описывать и изучать реальные процессы и явления. Обучающиеся развивают логическое и математическое мышление, умение рассуждать и применять знания при решении различных задач.
Типовые задания, нацеленные на познавательные результаты
Математика создаёт важнейший инструментарий для развития у детей познавательных универсальных действий. Именно на этих уроках широко используются заданий для развития таких важнейших мыслительных операций, как анализ, синтез, классификация, сравнение, аналогия.
Задание 1. Определение смежных углов через классификацию взаимного расположения углов
Цель: формирование умений: выделять существенные признаки, классифицировать, делать выводы и умозаключения, давать определение понятиям.
Возраст: 13–14 лет
Учебная дисциплина: математика (геометрия)
Форма выполнения: творческая работа учащихся – демонстрационная модель.
Описание задания:
Шаг 1: Выбрать рисунки (рис. 1), на которых углы имеют общую сторону. (Те рисунки, которые не поддаются данной классификации убираем)
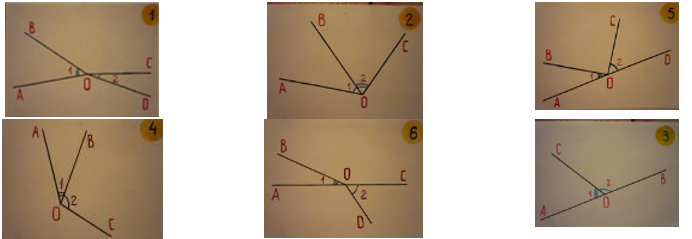

Рис. 1. Примеры для первого задания
Шаг 2. Из оставшихся рисунков (Рис.2) выбрать те, у которых стороны являются дополнительными полупрямыми.
 Рис. 2. Углы с общей стороной
Рис. 2. Углы с общей стороной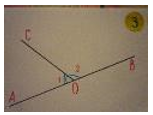 Рис. 3. Смежные углы
Рис. 3. Смежные углыВ результате классификации углов по их взаимному расположению остаются углы, которые называются смежными (Рис.3). Что это за углы? Учащиеся формулируют определение смежных углов
Задание 2. Мотивация изучения темы «Смежные и вертикальные углы». (По методике «Технология личностно ориентированного урока», автор В. В. Шоган) [2].
Цель: выполнение заданий, непосредственно связанных с определением последовательности действий по решению задач на построение.
Возраст: 13–14 лет
Учебная дисциплина: математика (геометрия)
Форма выполнения: задания, формирующие навыки определения видов углов, и их классификацию
Описание задания:
а) Воспоминание.
Цель: включение школьников в работу, позволяет учителю в нетрадиционной форме проверить их знания, прочность и глубину усвоения пройденного, выявить, какие именно вопросы нуждаются в разъяснении и закреплении.
В начале урока учащимся предлагается плакат с изображением различных углов.
Задание: «Вспомнить какие виды углов вы знаете и найти эти углы. Объяснить свой выбор»
б) Интрига
Цель: Формирование мотива, желания перейти на новую ступень от одного состояния к другому.
- Обратите внимание на взаимное расположение углов. А можно ли придумать классификацию по их взаимному расположению?
(углы, полученные пересечением прямых, углы, имеющие общую сторону, углы две стороны которых лежат на одной прямой и т. д.)
- Сегодня расширим круг своих знаний об углах, которые имеют определенное взаимное расположение, введем понятия смежных и вертикальных углов.
Типовые задания, нацеленные на личностные результаты
Научный математический язык позволяет описывать реальные процессы и явления. Математика – важное средство коммуникации в формировании речевых умений, которые неразрывно связаны с личностными результатами. В результате изучения предметной области «Математика и информатика» обучающиеся развивают логическое и математическое мышление, получают представление о математических моделях; овладевают математическими рассуждениями; учатся применять математические знания при решении различных задач и оценивать полученные результаты; овладевают умениями решения учебных задач; развивают математическую интуицию [1]. Работа с математическим содержанием учит уважать и принимать чужое мнение, если оно обосновано. Таким образом, работа с математическим содержанием позволяет поднимать самооценку учащихся, формировать у них чувство собственного достоинства, понимание ценности своей и чужой личности. С этой точки зрения на уроках полезны задания ориентированы на достижение личностных результатов. Такие которые они предлагают не только найти решение, но и составить самостоятельно задачу по изученной теме или подготовить проект.
Задание 1. Определить какие типы задач можно составить, зная определение и свойство смежных углов.
Цель: Учащиеся учатся анализировать, доказывать, убеждать. Формируется умение высказывать свое мнение. Учебно-познавательный интерес к новому учебному материалу и способам решения новых задач. Задания ориентированы на достижение личностных результатов, так как они предлагают не только составить задачи, но найти решение и обосновать его, основываясь только на фактах. Работа с математическим содержанием учит уважать и принимать чужое мнение, если оно обосновано.
Возраст: 13–14 лет.
Учебная дисциплина: математика (геометрия, алгебра).
Форма выполнения: групповая работа учащихся.
Материалы: Демонстрационный материал: «Виды задач».
Описание задания:
Учащимся предлагается вспомнить основные типы задач.
Класс делится на две группы.
Первая группа должна придумать задачи типа «целое – части».
Этот тип задачи ребята знают: известны части – найти целое; известны часть и целое – найти другую часть. Новый материал: Сумма смежных углов равна 180о. Сумма смежных углов – целое, градусная мера каждого угла – часть.
Вторая группа – задачи, решаемые с помощью уравнения. Когда в условии задачи дано сравнение углов.
После того как предложенные задачи будут решены и оценены учащимися других групп. Ребята выполняют следующее задание: «Найти в учебнике подобные задачи».
Обычно на уроках учащиеся с удовольствием составляют задачи. В результате приходит осмысление определения свойств геометрических фигур и способов решения.
Задание 2. Сконструировать демонстрационную модель смежных углов.
Цель: Развитие творческих способностей. Посредством подобных заданий у ребенка происходит развитие речи, мышления и воображения, что неразрывно связано с формированием его личностных качеств.
Возраст: 13–14 лет
Учебная дисциплина: математика (геометрия).
Форма выполнения: творческая работа учащихся – демонстрационная модель.
Описание задания:
Первый этап – этап планирования. Это этап подготовки проекта. Определить цель проекта – спроектировать и создать демонстрационную модель смежных углов. План выполнения проекта: определить материалы и средства, необходимые для реализации проекта, сроки, форма представления готового результата.
Второй этап – этап выполнения проекта. Когда вся необходимая информация для выполнения проекта получена, ее необходимо обработать. То есть наступает этап обобщения информации. Здесь необходимо привести полученные данные в систему, обобщить их.
На последнем этапе работы над проектом необходимо поработать над тем, как представить результат всей работы остальным участникам. Здесь надо описать все этапы работы, методы и приемы, которые использовались. Выявить трудности, с которыми столкнулись, как они были преодолены.
В результате появляется демонстрационный материал для уроков математики в виде презентации, таблицы-плаката, подвижная модель и др.
Типовые задания, нацеленные на коммуникативные
универсальные учебные действия
Задание 1. Построить смежные углы.
Цель: формирование:
- умения действовать с учетом позиции другого и уметь согласовывать свои действия;
- умения определять цели коммуникации, оценивать ситуацию;
- опыта использования речевых средств для регуляции умственной деятельности.
Возраст: 13–14 лет.
Учебная дисциплина: математика (геометрия).
Форма выполнения: работа в парах, практическое задание.
Описание задания:
Применяя определение смежных углов, учащиеся открывают способ построения этих углов. Работая в парах, вырабатываю алгоритм построения смежных углов. Парам предлагаются различные задачи:
Задача 1: Постройте смежные углы ∠АОС и ∠СОВ, если дан развернутый угол АОВ
Задача 2. Постройте смежные углы ∠АОС и ∠СОВ, если дан угол ∠СОВ. Составьте алгоритм построения смежных углов.
В результате учащиеся формулируют алгоритмы построения смежных углов, объясняя последовательность выполнения заданий.
Задание 2. Определение цели работы через формирование декларативных и процедурных знаний.
Цель: Организация ситуации, позволяющей школьникам вместе с учителем выбрать план деятельности на уроке.
Возраст: 13–14 лет
Учебная дисциплина: математика (геометрия).
Форма выполнения: работа в группах.
Описание задания:
Система подводящих диалогов позволяет учащимся самостоятельно, основываясь на имеющихся у них знаниях спланировав свою деятельность, и оценить результат, проверив его.
В начале урока, после определения темы урока, предложить группам учащихся составить план изучения данной темы. При изучении темы «Смежные и вертикальные углы» необходимо определить план работы. Для этого первая группа должна продолжить предложение: «Изучив тему я должен узнать, что…» (декларативные знания). При изучении новых понятий подросток знает, что он должен узнать определение, свойства, историческую справку (что такое смежные и вертикальные углы, и их свойства)
Вторая группа «Я должен узнать, как…» (процедурные знания). Учащиеся знают, что должны научиться применять определение и свойства геометрических фигур для решения текстовых задач и построения (как решить задачу, как построить углы).
Типовые задания, нацеленные на регулятивные
универсальные учебные действия
Данный вид заданий рассмотрим на примерах:
- Исследовательской работы на занятие математического кружка по теме «Делимость чисел».
- Изучения новой темы на уроке алгебры по теме «Сложение дробей с разными знаменателями».
Задание 1. Решето Эратосфена
Цель: Использование заданий, позволяющих научить школьников самостоятельному применению знаний в новой ситуации, т. е. сформировать регулятивные универсальные учебные действия.
Возраст: 13–14 лет
Учебная дисциплина: математика (алгебра).
Форма выполнения: практическая работа с использованием интерактивной доски. Занятие математического кружка.
Описание задания: Предлагается исследовательская работа: Используя алгоритм Эратосфена, найдите все простые числа среди первых 100 натуральных чисел.
На интерактивной доске представлена таблица первых 100 натуральных чисел:
Таблица 1
Первые 100 натуральные числа
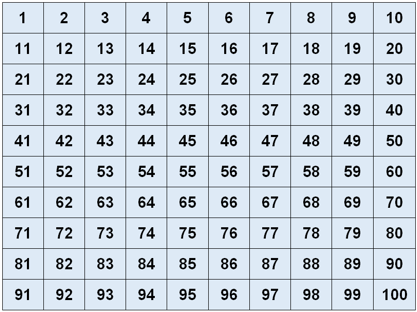

Учащиеся закрашивают число 1 и числа, которые делятся на 2 после закрашивания замечают, что в натуральном ряду чисел каждое второе делится на 2, каждое третье – на 3, каждое четвертое – на 4 и т. д. В результате получают «решето», на котором остаются простые числа:
Таблица 2
Простые числа среди первых 100 натуральных чисел.
Решето Эратосфена


В процессе работы, учащиеся предлагают различные подходы выполнения данного задания, вырабатывая совместный более рациональный подход.
Задание 2. Сложение дробей с разными знаменателями.
Цель: Использование заданий, позволяющих формировать у учащихся уверенности в своей возможности решать новые задачи, используя свой опыт; определять план выполнения для достижения поставленной цели.
Возраст: 13–14 лет
Учебная дисциплина: математика (алгебра)
Форма выполнения: изучение новой темы «Сложение дробей с разными знаменателями», построенная на вопросах, ответы на которые учащиеся должны найти сами.
Описание задания:
1 этап – воспоминание.
Задание: Найти значение выражения: а) ; б) ; в) .
Задания первой группы на повторение ранее изученной темы «Сложение дробей с одинаковыми знаменателями. При решении прослеживается аналогия между решением числовых и буквенных выражений.
2 этап – интрига.
Вычислить: а) ; б)
Во второй группе задания по теме «Сложение дробей с разными знаменателями». Если первое из них числовое выражение и учащиеся знают способ решения, а вот второе – это уже интрига. Пример нового уровня. Аналогия же предыдущих примеров помогает школьникам выстроить план решения в соответствии с планом решения примера а.
Ссылки на источники
1. Федеральный государственный образовательный стандарт основного общего образования (утв. приказом Министерства образования и науки РФ от 17 декабря 2010 г. N 1897)
2. Шоган В.В., Технологии личностно ориентированного урока: учебно-методическое пособие для учителей, методистов, классных руководителей, студентов педагогических заведений, слушателей ИПК. – Ростов на Дону: Издательство «Учитель», 2003.
2. Шоган В.В., Технологии личностно ориентированного урока: учебно-методическое пособие для учителей, методистов, классных руководителей, студентов педагогических заведений, слушателей ИПК. – Ростов на Дону: Издательство «Учитель», 2003.
Kansina Claudia G.,
mathematics teacher, MBOU Nikolskaya SOSH, Nikolskoe, Sovetsky District, Altai Krai
Common tasks to develop generic training action
Abstract. This article discusses common tasks on a universal educational actions, which were presented on the lessons of geometry while studying the theme “Adjacent and vertical angles", algebra – "Fractions with different denominators", and classes of mathematical mug – "Signs of divisibility"
Keywords: adjacent angles, vertical angles, signs of divisibility, prime numbers, Eratosthenes.
