Регулятивные УУД.
Предлагаемые виды организации работы на уроке, направлены на создание проблемной ситуации, для решения которой необходим анализ и соотнесение известных фактов по теме с теми, что создают проблему. Поиск и выделение необходимой информации, знаково-символические и логические действия приводят к постановке и решению проблемы. Такие формы работы я использую на уроках изучения нового материала и вторичного закрепления тем, когда трудность заданий возрастает и для их выполнения требуется использовать комбинированные методы решения.
1. Урок алгебры и начал анализа в 10 классе. Решение иррациональных неравенств. На предыдущих уроках отрабатывались навыки решения неравенств вида: , где а- действительное число. На этом уроке предстоит научиться решать неравенства, в правой части которых рациональная функция от переменной, а также неравенства, содержащие иррациональную функцию как в левой так и в правой части. Итогом работы должны стать алгоритмы решения неравенств, записанные в виде равносильных неравенств и их систем. Рассмотрим подробнее фрагмент урока на примере неравенства вида
На интерактивную доску выводятся неравенства вида , решенные на предыдущих уроках, причем, апринимает в них положительные, отрицательные и нулевое значения. Учащиеся анализируют все случаи, выдвигают гипотезы, обсуждают предложения друг друга. В ходе дискуссии рождается условие равносильного перехода от иррационального неравенства к рациональному:, но записано это условие пока для конкретного неравенства.
Если дискуссия зашла в тупик, учитель предлагает ещё одно или несколько неравенств с числом в правой части, помогающее правильно проанализировать все случаи. Затем решается неравенство и записывается обобщенный вывод в виде теоремы.
Аналогично поступают и с остальными двумя видами неравенствами.
2. Урок алгебры в 8 классе. Решение рациональных неравенств.
К этому уроку учащиеся умеют решать неравенства I степени, записывать ответ для неравенств I и II степени с графического изображения функции.
Учитель предлагает решить неравенство вида: .
Чтобы продумать план действий, учащиеся решают неравенство I степени двумя способами и неравенство II степени графическим способом.
Анализируя полученные результаты, выделяют проблемы:
- найти точки пересечения с осью Ох,
- определить знаки функции из левой части в полученных промежутках.
На следующих уроках задание усложняется: левая часть представлена в виде многочлена; при разложении на множители появляются корни четной кратности; наконец левая часть является дробно-рациональной функцией.
Результатом этой серии уроков является алгоритм решения рациональных неравенств.
Личностные, коммуникативные УУД.
На уроках математики организовать работу, развивающую личностные и коммуникативные качества можно в групповой работе, либо организовав диспут.
Такие формы работы я использую на уроках самостоятельного изучения теоретического материала, либо уроках обобщения и систематизации знаний по теме. Предлагаю организацию урока и подготовительную работу, которую нужно провести с учащимися, чтобы урок достиг цели и настроил учащихся на активную работу на всех этапах урока. В нашей школе используется балльная система оценок, но её не трудно перевести в 5-ти балльную, предварительно обсудив с учащимися критерии.
Урок систематизации и обобщения знаний по геометрии в 8-м классе.
В таких уроках главное - подготовительный этап.
При подготовке этого мероприятия учащиеся на уроке разрабатывают критерии оценки выступления, делят курс 8 класса на три равнозначные темы, обсуждают возможные варианты презентаций, делятся на группы, выбирают капитанов команд. В зависимости от подготовки класса, задания (темы), можно дать заранее, а можно на уроке. В качестве помощи в подготовке презентации стоит оговорить регламент выступления. Обязательно следует посвятить следующий урок анализу выступлений, дать высказаться всем желающим, предоставить возможность командам дать самоанализ выступления, участия членов команды в работе. Регулярность таких уроков вырабатывает умения взаимодействовать, сотрудничать со сверстниками и взрослыми, слушать, ориентироваться в межличностных отношениях, вырабатывает владение монологической речью, научной терминологией, работе с различными видами информационных источников. На урок желательно пригласить в качестве жюри коллег.
Предлагаю возможный вариант протокола выступлений:
Критерии оценки представления темы
по курсу геометрии в 8-м классе.
|
№
|
Критерии
|
Оценка
|
|
1
|
|
Информативность презентации
|
10
|
|
1.а
|
Выявление взаимосвязей между рассматриваемыми понятиями, фактами, выводами
|
|
1.б
|
Структурированность и логичность текста и выступления, презентации
|
|
1.в
|
Корректность и полнота выводов (уровень общения)
|
|
1.г
|
Существенность выделенных признаков подобия и различия
|
|
2
|
|
Свободное владение темой, умение рассуждать при ответах на вопросы
|
7
|
|
3
|
|
Активность команды
|
5
|
|
4
|
|
Дополнительный материал, включая выводы, полученные при ответах на вопросы
|
5
|
|
5
|
|
Умение задавать вопросы.
|
3
|
|
6
|
|
Взаимоотношения между членами команды.
|
5
|
|
|
|
ИТОГО:
|
35
|
Познавательные УУД
На уроках математики познавательные и регулятивные учебные действия неотделимы друг от друга. Поэтому я выбрала исследовательскую работу в качестве примера познавательных действий. При проведении такой работы важно: планирование работы учащегося и его совместной работы с учителем. Это нужно оформить в виде календарного графика, в который можно вносить коррективы.
План подготовительного этапа:
1. Подбор информационных источников
2. Работа с источниками.
3. Составление тематического плана выступления.
4. Отбор материала.
5. Подготовка презентации.
6. Репетиция выступления.
1. Исследовательская работа по теме: «Геометрия Лобачевского».
Аннотация.
Данную работу целесообразно проводить в 9-м классе, т. к. учащиеся к этому времени привыкли к разделу математики – геометрия. Структуре этого курса. Именно на этом предмете подробно демонстрируется процесс создания любой науки: аргументируется необходимость введения начальных понятий, вводится аксиоматика, на основании этих фактов строятся выводы, называемые теоремами.
Не имеет смысла приводить полный текст исследовательской работы, как один из вариантов её содержания привожу вступление, оглавление, основные фрагменты и список литературы. Объем и глубина изучения зависит от желания, возможностей учащегося.
В работе раскрывается неоднозначный подход к построению геометрии, и в то же время рассматриваются три необходимых условия для создания любой системы аксиом: непротиворечивости, минимальности, полноты.
Особый акцент в работе сделан на различие в определении параллельности прямых, также проводится сравнение некоторых теорем в геометриях Лобачевского и Евклида:
|
В геометрии Эвклида
|
В геометрии Лобачевского
|
|
Сумма углов любого треугольника постоянна и равна 2d.
|
Сумма углов меняется от треугольника к треугольнику и всегда меньше 2d.
|
|
Сумма углов всякого выпуклого четырехугольника равна 4d.
|
Сумма углов выпуклого четырехугольника меньше 4d. Так что, в частности не существует прямоугольников.
|
|
Ко всякому треугольнику можно построить подобный, но не равный ему треугольник.
|
Если три угла одного треугольника соответственно равны углам другого треугольника, то они равны.
|
|
Вокруг всякого треугольника можно описать окружность
|
Не вокруг всякого треугольника можно описать окружность.
|
Вступление
Проблемами, связанными с разного рода геометриями ученые занимались давно. Изначально создавался фундамент из аксиом, на котором Евклид построил свою, непротиворечивую геометрию. Однако сам Евклид заметил некоторые проблемы, которые не смог решить. Это проблема пятого постулата, благодаря которой и существует геометрия Лобачевского. В реферате рассмотрен процесс возникновения геометрии, различные геометрические пространства, некие проблемы в развитии геометрии как науки. Геометрия Лобачевского, с момента создания, привлекала к себе внимание. Она явилась неожиданным решением проблемы пятого постулата, над которым долго бились многие ученые. В работе использованы работы авторитетных ученых.
2. Урок по теме «Экскурсия по таблице квадратов натуральных чисел»
На примере этого мероприятия я хочу показать, как использование анимационных презентаций позволяет повысить интерес, активность учащихся, а значит обеспечить их участие в полемике, выступлениях.
Предлагаемый урок разработан учителями математики НОУ «Школа им. А. М. Горчакова» (Санкт-Петербург) Кутыгиной Татьяной Владимировной и Лейкиной Тамарой Николаевной.
Данное занятие рекомендуется проводить в пятом классе. Оно готовит ребят к введению понятия степень с натуральным показателем. В результате проведенного урока ребята учатся ориентироваться в таблице квадратов чисел, встречаются с «числами–перевёртышами», «палиндромическими парами». Установленные закономерности и взаимосвязи между квадратами чисел, самими числами и их квадратами способствуют запоминанию таблицы.
Название занятия обусловлено тем, что за время урока ученики, составив таблицу квадратов чисел от 11 до 32, несколько раз обращаются к ней и открывают новое для себя.
Этот урок способствует развитию умения анализировать, различать информацию, требующую запоминания и понимания, выдвигать гипотезы, делать выводы на основании полученных фактов.
Ключевые слова: квадрат числа, сумма последовательных нечётных чисел, палиндромические пары.
Цели урока:
- вскрыть закономерности между числами и их квадратами в таблице квадратов натуральных чисел;
- развивать умение анализировать, обобщать, делать выводы, строить гипотезы;
- показать через связь искусства с математикой гармонию мира.
Задачи:
- научить использовать распределительное свойство умножения относительно сложения и вычитания для вычисления квадрата числа;
- установить окончания квадратов чисел;
- получить рекуррентную формулу вычисления квадратов чисел;
- установить зависимости: между суммой первых последовательных нечётных чисел и их количеством; между разностью квадратов двух последовательных чисел и суммой этих чисел;
- научить возводить в квадрат числа, оканчивающиеся на пять.
Метод:
- проблемно-поисковый.
Формы работы на уроке:
- групповая;
- фронтальная.
Подготовка к уроку:
- разбить учащихся на группы;
- подготовить для каждой группы задания к слайду № 3: несколько двузначных чисел для заполнения таблицы квадратов чисел;
- распечатать материалы приложений.
Оборудование:
- интерактивная доска.
Ход урока
Этап I
Мотивация к теме урока.
 Слайд № 1
Слайд № 1Учитель рассказывает о картине русского художника Н. П. Богданова-Бельского «Устный счёт», написанной в 1895 году.
На картине изображена деревенская школа XIX века во время урока устного счёта. Учитель – реальный человек, Сергей Александрович Рачинский. Он был профессором Московского университета, ботаником и математиком. На волне народничества в 1872 году Рачинский вернулся в родное село Татево, где создал школу, с общежитием для крестьянских детей, разработал уникальную методику обучения устному счёту. Эпизоду из жизни школы с творческой атмосферой, царившей на уроках, посвятил своё произведение Богданов-Бельский, бывший сам учеником Рачинского.
На доске написана задача, которую необходимо решить ученикам:
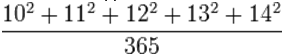
Решить устно задачу учащимся поможет этот урок.
По желанию учитель может сообщить факты из биографии С.А. Рачинского (Приложение 3)
Этап II
Заполнение таблицы квадратов натуральных чисел.
Учитель предлагает ребятам начать знакомство с таблицей квадратов с нахождения окончаний квадратов натуральных чисел. В ходе дискуссии выясняется, что достаточно рассмотреть натуральные числа первого десятка.
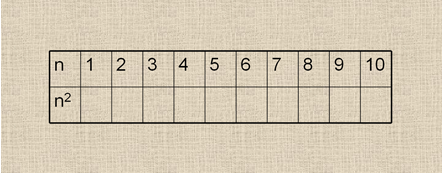
Слайд № 2Полученные результаты фиксируются в таблице на доске и закрепляются в упражнении: могут ли быть квадратами натуральных чисел следующие числа?
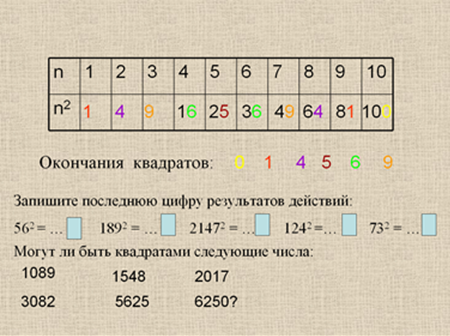
Слайд № 2На следующем слайде предъявляется незаполненная таблица.
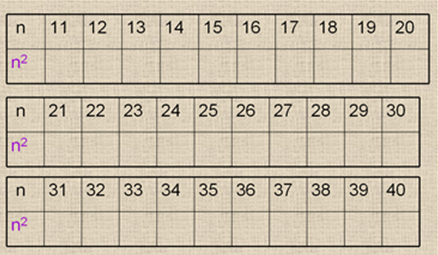
Слайд № 3
Учитель предлагает заполнить её и для этого использовать распределительное свойство, перейдя к «круглым» числам.
На слайде с помощью анимации показан пример такого вычисления.
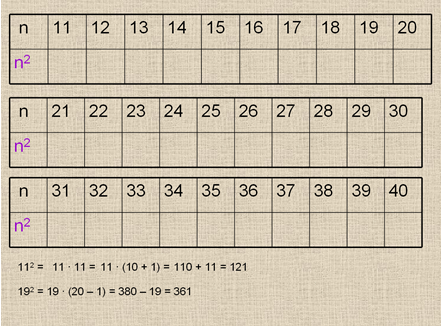 Слайд № 3
Слайд № 3После этого группам учащихся раздаются задания на вычисление квадратов натуральных чисел от одного до тридцати двух.
Полученные результаты заносятся в таблицу.
Этап III
Выявление закономерностей между числами в таблице.
На следующем слайде представлена заполненная таблица. Ребятам предлагается рассмотреть внимательно числа и найти закономерности, помогающие запомнить квадраты чисел.
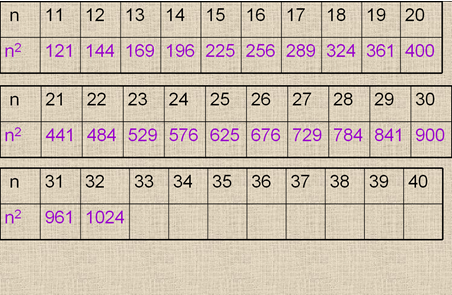
Слайд № 4
В ходе обсуждения называются пары квадратов 12 и 21: 144 и 441; то же самое подмечается для квадратов 13 и 31: 169 и 961.
Анализируя следующие числа и их квадраты, ребята убеждаются, что дальнейший поиск таких же закономерностей бесполезен: 142 = 196, а 412 = 1681, и уже, начиная с числа 32, квадраты всех следующих чисел являются четырехзначными числами. Проводится аналогия с палиндромами в русском языке. Можно дать задание группам: привести примеры палиндромов в русском языке.
Полученные выводы отмечаются в таблице. Далее подмечается, что квадраты чисел 13 и 14 получаются перестановкой двух последних цифр, квадраты 24 и 26 отличаются на 100, 23 и 27 – на 200, 22 и 28 – на 300.
На этом же слайде с помощью анимации появляются полученные в диалоге факты.
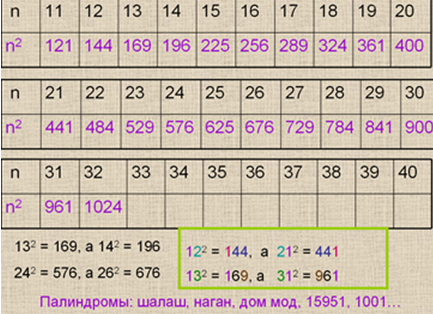
Слайд № 4Следующий слайд представляет собой ту же таблицу, но квадраты некоторых чисел пропущены. Группам дается задание: анализируя два последовательных числа и их квадраты в таблице, попробовать заполнить пропущенные клетки и обобщить формулу нахождения квадрата числа, следующего за числом
n. На этом же слайде анимационно показан выбор чисел:
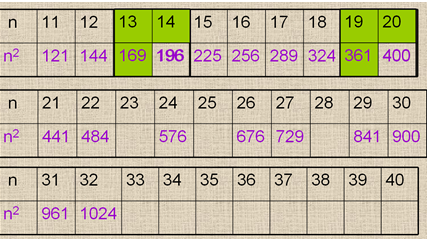
Слайд № 5и формула:
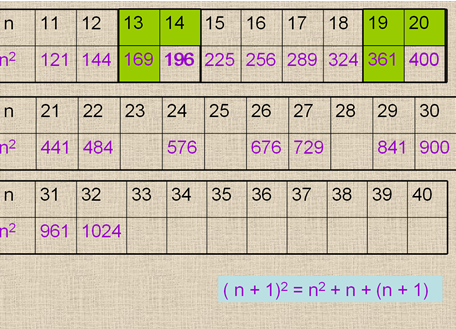
Слайд № 5
Можно пояснить ребятам, что с этой формулой они познакомятся в курсе алгебры 8 класса, показать, как она записывается и читается.
Геометрическая интерпретация квадрата числа как площади квадрата со стороной, равной числу, приводится на следующем слайде.
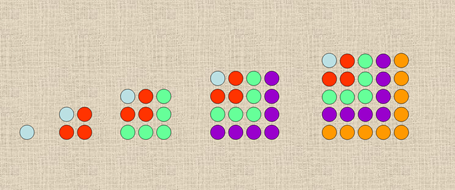
Слайд № 6
Квадраты, составленные из цветных кружочков, появляются постепенно, что помогает заметить закономерность при составлении квадрата следующего числа.
Далее ребятам предлагается записать площадь каждого квадрата в виде суммы предыдущего и количества новых кружков. Полученные результаты появляются на слайде.

Слайд № 6
Далее предлагается обобщить полученный результат в виде формулы. Ребятам сообщается, что выводится данная формула с помощью метода математической индукции, который изучается в профильных математических классах, на факультативах, в кружках. Формула выражает зависимость между квадратом числа, суммой первых последовательных нечётных чисел, количество которых равно самому числу, или последовательный ряд нечётных чисел.
Закрепить применение формулы предлагается, вычислив квадраты некоторых чисел и сверив полученные результаты с данными в таблице квадратов чисел.
Выразив число, на которое отличаются квадраты двух последовательных чисел, ребята замечают, что оно равно сумме самих чисел. Учитель знакомит их с названием этой формулы и сообщает им, что проходить формулы сокращенного умножения они будут на уроках алгебры в 8 классе. Все эти факты появляются на слайде.

Слайд № 6
Этап III
Квадраты чисел, оканчивающихся на 5.
Во время работы со слайдом № 7 ребята подмечают закономерности в квадратах чисел, оканчивающихся на пять. Сначала они вычисляют квадраты 15; 25; 35 и заносят их в таблицу.

Слайд № 7
Далее обращают внимание на окончания квадратов.
 Слайд № 7
Слайд № 7После этого пытаются записать формулу зависимости количества сотен в квадрате числа от количества десятков в самом числе.

Слайд № 7
 Слайд № 7
Слайд № 7В ходе обсуждения появляется формула для вычисления квадрата числа.
Слайд № 7
Ребятам предлагается проверить правильность формулы, вычислив квадраты 45; 55; 65.
На этом работа с таблицей заканчивается. В качестве итога предлагается задание: «Впишите недостающие цифры так, чтобы равенство было верным». Его выполняют совместно с учителем. На слайдах показана последовательность анализа квадрата числа с первой цифрой 2 и окончанием квадрата равным 4. Далее анализируются следующие два задания, в которых совпадает цифра в разряде десятков самого числа и окончания квадратов, но квадраты числа отличаются количеством цифр. Аналогичное задание раздаётся ребятам в качестве домашнего задания, а также две задачи, имеющие отношение к теме этого урока. (Приложение 2)
 Слайд № 8
Слайд № 8 Слайд № 8
Слайд № 8 Слайд № 8
Учитель объявляет результативность работы в группах и комментирует книгуД. С. Фаермарка «Задача пришла с картины», возвращаясь к задаче с картины, которую предлагает решить.
Комментарии.
В Приложении 1 предлагается игра «Домино», которую нужно заранее подготовить по указанному образцу. Выбрать для неё время на уроке достаточно сложно из-за его плотности, поэтому учитель может воспользоваться ею по своему усмотрению.
Предложенный урок проводили два учителя, присутствуя на уроке одновременно. Это очень удобно, т.к. позволяет контролировать работу в группах.
Приложение 1
Впишите недостающие цифры так, чтобы равенство было верным:
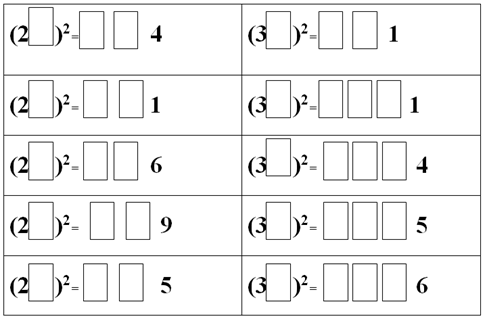
Дополнительные задачи.
1. Номер квартиры
Рассеянный математик, переселившийся в новый район, забыл номер своей квартиры. Он лишь помнил, что номер двузначный, является разностью квадратов двух чисел, меньшее из которых равно цифре десятков и вдвое больше числа единиц номера квартиры.
Можно ли по этим данным вспомнить номер квартиры?
2. Спидометр
Находясь в пути за рулём, шофёр заметил, что на спидометре высветилось число 15951 (км). Ровно через два часа он обратил внимание на то, что на спидометре опять получилось число, которое можно прочесть справа налево и слева направо одинаково. (Такие числа называются палиндромами). Какова была средняя скорость автомобиля в эти два часа?
Ссылки на источники
1. Александров П. С., Что такое неэвклидова геометрия. M.: АПН, 1950.
2. Винберг Э. Б., О неевклидовой геометрии. «Математика», № 3, 1996.
3. Ефимов Н. В.,Высшая геометрия. – 7-е изд. – М.: ФИЗМАТЛИТ, 2004
 Слайд № 1
Слайд № 1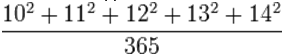



 Слайд № 3
Слайд № 3







 Слайд № 7
Слайд № 7
 Слайд № 7
Слайд № 7
 Слайд № 8
Слайд № 8 Слайд № 8
Слайд № 8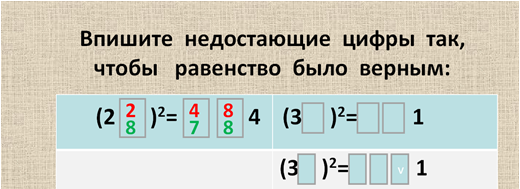
 Дополнительные задачи.
Дополнительные задачи.