Несмотря на смену поколений образовательных стандартов [1], современность применяемых методик обучения математике школьников, у школы навсегда останется одна из основных задач: воспитать вдумчивого, творчески мыслящего, заинтересованного в своем труде человека. Ребенок, обучаясь, должен иметь возможность творить, фантазировать на доступном ему уровне и в известном мире понятий. А если он к тому же свободен от боязни допустить ошибку, то все это станет залогом успеха начинающейся творческой деятельности. Несомненно, то творчество невозможно без умения наблюдать и примечать особенности явлений, чисел, понятий, свойств фигур.
Геометрия незаслуженно считается одним из самых сложных школьных предметов. Но именно при изучении этого раздела математики у учащихся формируются различные универсальные учебные действии, которые впоследствии способствуют развитию интеллектуальной активности личности, способной к поисковой и исследовательской деятельности, творческой самореализации, развитию творческого мышления со стандартизированной программой.
Чем выше уровень творческого развития ученика, тем выше уровень его общего умственного развития, тем выше его работоспособность. Именно поэтому одна из задач, которые ставит перед собой современный педагог – это развитие творческих способностей ученика.
Целенаправленное развитие теоретического мышления учащихся следует сочетать с совершенствованием творческого мышления.
Творческое мышление – высший уровень развития личности. Дж. Гилфорд считал, что уровень развития креативности (творческого мышления) определяется доминированием в мышлении четырех особенностей.
Оригинальность высказанных идей, стремление к интеллектуальной новизне,
семантическая гибкость, т.е. способность видеть объект под разными углами зрения, способность обнаружить возможность нового использования данного объекта, ну и, конечно, творческому мышлению свойственна образная адаптивная гибкость [2].
В соответствии с особенностями и целями применения разного рода задач, можно предложить следующую модель урока, направленного на развитие творческих способностей, как в системе специальных уроков развития, так и занятий в системе дополнительного образования по математике. Его структура может включать в себя последовательные этапы:
- Актуализация предыдущих знаний;
- Развитие психических механизмов, лежащих в основе творческих способностей учащихся (памяти, внимания, мышления, воображения);
- Выполнение развивающих частично-поисковых задач;
- Решение творческих задач, которые можно разделить на два типа: творческие задания и задачи повышенной трудности интегративного характера;
Для осуществления развивающих целей обучения необходимо активизировать познавательную деятельность, создать ситуацию заинтересованности.
Используя проблемы развития математических способностей учащихся, психолог В.А. Крутецкий приводит типы задач для развития активного самостоятельного, творческого мышлении, например задачи с несформулированным вопросом или задачи с недостающими данными.
В задачах такого типа отсутствуют некоторые данные, вследствие чего дать точный ответ на вопрос задачи не представляется возможным. Однако, ученик должен проанализировать задачу и доказать, почему нельзя дать точного ответа на вопрос задачи, чего не хватает, что надо добавить. В скобках указываются пропущенные данные [3].
И здесь задача учителя найти простые и удобные средства для практической реализации всех этапов инновационных педагогических технологий в многоуровневой системе НФТМ – ТРИЗ (система непрерывного формирования творческого мышления и развития творческих способностей обучаемых) [4].
Рассмотрим урок по геометрии в 7 классе по теме: «Сумма углов треугольника. Внешний угол треугольника», разработанного в соответствии со структурой креативного урока.
Цели урока:
Образовательные:
1) Практическим путем выяснить чему равна сумма углов треугольника, познакомиться с формулировкой теоремы о сумме углов треугольника, доказать теорему, доказать следствия из теоремы, научиться применять изученную теорему при решении задач;
Развивающие:
1) совершенствовать умения логически и творчески мыслить и выражать свои мысли вслух;
2) стимулировать познавательную деятельность учащихся постановкой проблемного задания, оценкой и поощрением;
Воспитательные:
1) воспитывать у учащихся стремление к совершенствованию своих знаний;
2) воспитывать интерес к предмету.
Ход урока
1. Организационный момент.
2. Мотивация урока. Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. В строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах. Мы рассмотрели виды треугольников, знаем некоторые их свойства и сегодня мы продолжим изучение свойств треугольника, независимо от его вида.
3. Актуализация опорных знаний.
1) Вспомните, какая фигура называется треугольником.
2) Какими могут быть треугольники в зависимости от величины углов?
3) Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?
4) Какой треугольник называется тупоугольным?
5) Может ли в треугольнике быть два тупых угла? Объяснить ответ.
6) Параллельны ли прямые т и n?
7) Бывают ли треугольники с двумя прямыми углами? С двумя тупыми углами? С прямым и тупым углом? Как это обосновать? Сделать рисунок. К доске выходит ученик и выполняет следующие рисунки:
Далее идет коллективное обсуждение: Лучи ВА и СО, КТ и ОН. КЕ иPL пересекаются, значит, треугольник не получится. Сумма односторонних углов в I случае больше, чем 1800, во II случае также больше, чем 1800, а в III случае — равна 180°. В III случае прямые параллельны, а в первых двух случаях прямые расходятся. Делают вывод, что треугольник не может иметь два тупых или два прямых угла. А также в треугольнике не может быть одновременно один тупой и один прямой углы.
Далее идет коллективное обсуждение: Лучи ВА и СО, КТ и ОН. КЕ иPL пересекаются, значит, треугольник не получится. Сумма односторонних углов в I случае больше, чем 1800, во II случае также больше, чем 1800, а в III случае — равна 180°. В III случае прямые параллельны, а в первых двух случаях прямые расходятся. Делают вывод, что треугольник не может иметь два тупых или два прямых угла. А также в треугольнике не может быть одновременно один тупой и один прямой углы.Решить по учебнику задачи стр.66, № 205, 208.[5]
4. Изучение нового материала.
Практическое задание учащимся.
1) Измерьте с помощью транспортира углы треугольников (заранее раздать учащимся модели треугольников) и найдите их сумму (каждый ученик говорит свой результат)
Что получилось? Сумма углов треугольника равна 180°?
2) У вас у каждого лежит на парте модель треугольника. Пронумеруйте его углы. Составьте угол из углов треугольника, определите вид этого угла и найдите его градусную меру.
Оторвите углы треугольника и моделируйте.
Какую закономерность вы заметили? (Сумма углов треугольника равна 180º). Случайно ли сумма углов треугольников оказалась равной 180º или этим свойством обладает любой треугольник?
Создание проблемной ситуации. Учащиеся понимают, что ответ они могут дать лишь наугад.
Как мы назовем утверждение, которое сформулировали? (Гипотезой).
Ребята высказывают свои соображения. Проблемный диалог с учащимися
А почему это утверждение мы назвали гипотезой? (Потому что мы практически это увидели, но не доказали).
Как убедиться, что гипотеза стала истиной, т. е. что она справедлива для любого треугольника? (Её надо доказать).
Как называется утверждение, справедливость которого надо доказать? (Теоремой).
Выскажите гипотезу. «Сумма углов любого треугольника равна 180°»
Гипотеза сформулирована. Чтобы она стала истиной – требуется доказать.
Итак, теорема
Формулировка: Сумма углов треугольника равна 180°
Дано: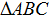
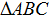
Доказать: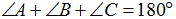 
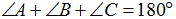
Доказательство:
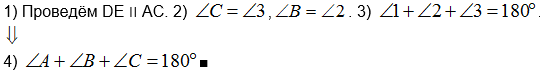
Впервые доказал теорему Пифагор, затем Евклид.
Закрепление теоремы в ходе устных упражнений по готовым чертежам.
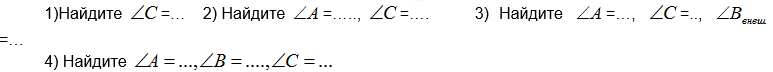
Введение понятия внешнего угла треугольника.
Внешним углом треугольника называется угол, смежный с внутренним углом треугольника.
Свойство внешнего угла треугольника: внешний угол треугольника равен
сумме двух внутренних углов, не смежных с ним.
5. Закрепление нового материала.
Решить по учебнику [5] № 223(б,г), 228 (а,в), 234.
6. Физкультминутка.
Одолела вас дремота,
(Зеваем.)
Шевельнуться неохота?
Ну-ка, делайте со мною
Упражнение такое:
Вверх, вниз потянись,
(Руки вверх, потянулись.)
Окончательно проснись.
Руки вытянуть пошире.
(Руки в стороны.)
Раз, два, три, четыре.
Наклониться — три, четыре
(Наклоны туловища.)
И на месте поскакать.
(Прыжки на месте.)
На носок, потом на пятку.
Все мы делаем зарядку.
7. Самостоятельная работа.
Тренировочные тесты по готовым чертежам (готовые чертежи могут быть как плакатными, так и частью электронной презентации)
1. Цель данного этапа решения задач: зафиксировать изученное учебное содержание во внешней речи. Работа идет устно.
Существует ли треугольник с углами:
а) 30˚, 60˚, 90˚ б) 46˚, 160˚, 4˚
в) 75˚, 80˚, 25˚ г) 100˚, 20˚, 55˚?
2.Устная работа по готовым чертежам.
Найдите углы треугольника.
Далее учителем ставится новая проблема:
Можно ли найти углы последнего треугольника? (Нет) При каких условиях можно находить углы треугольника? (Если известен вид треугольника, или градусная мера двух его углов).
3. Решение задач с письменным оформлением:
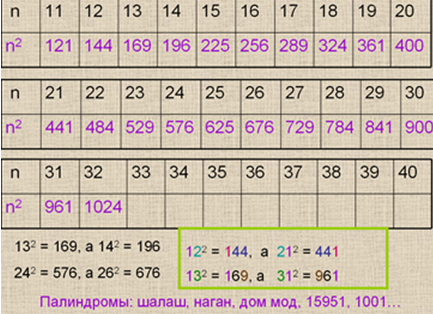
5. Решение задач – «паутинок», содержание которых предусматривает применение всех полученных знаний и умений на уроке.
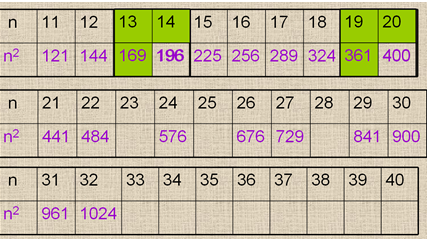
8. Итоги урока. Домашнее задание.
Выучить основные понятия и доказательство теоремы п.30,31. Решить № 224, 229.[5]
Резюме учителя: Вот и подошел к концу наш урок. Давайте подведем итоги. Мы выучили – …. Мы умеем – …Сделаем выводы – ….(заслушиваются ответы учащихся).
Разумеется, объем материала, предложенного к использованию на уроке, может варьироваться, но главная цель – выдержать структуру урока и по желанию учителя, а также по возможностям учащихся в качестве домашнего задания реально предложить учащимся ряд головоломок с геометрическим содержанием [5].
В целях развития логического мышления учащихся нужно предлагать им самостоятельно производить анализ, синтез, сравнение, классификацию, обобщение, строить индуктивные и дедуктивные умозаключения. Такая возможность предоставляется в условиях выполнения логически-поисковых заданий [5], которые обеспечат преемственность перехода от простых формально-логических действий к сложным, от заданий на репродукцию и запоминание – к истинно творческим.
Каждая текстовая задача и добрая половина других упражнений, представленных в учебниках геометрии и дидактических материалах, и есть своего рода проблемы, над решением которых ученик должен задуматься, если не превращать их выполнения в чисто тренировочную работу, связанную с решением по готовому, данному учителем образцу. Только в этом случае обучение математике в целом будет оказывать действенную помощь в решении образовательных, воспитательных и развивающих задач обучения, способствуя развитию познавательных способностей учащихся, таких черт личности, как настойчивость в достижении поставленной цели, инициативность, умение преодолевать трудности.
Таким образом, единственным качественным и плодотворным путем развития творческого мышления учащихся становится максимально полное раскрытие их потенциальных возможностей, природных задатков, а учителю необходимо создать модель полноценной развивающей деятельности для учащихся, чтобы потенциал реализовался.
Ссылки на источники
- Федеральный государственный образовательный стандарт общего образования. - М. 2011. – с.4
- Утёмов В. В. Задачи открытого типа как средство развития креативности учащихся средней школы // Концепт: научно-методический электронный журнал официального сайта эвристических олимпиад «Совёнок» и «Прорыв». – 4 квартал 2011, ART 11-4-02. – Киров, 2011 г. – URL: http://www.covenok.ru/koncept/2011/11402.htm. – Гос. рег. Эл № ФС 77-46214. – ISSN 2225-1618.
- Крутецкий В.А. Проблема способностей в психологии: (В помощь лектору). – М.: Знание, 2011. – 62 с.
- Утёмов В. В., Зиновкина М. М., Горев П. М. У84 Педагогика креативности. Прикладной курс научного творче-ства: Учебное пособие. – Saarbrucken: Palmarium Academic Publishing, 2013. – 216 с. Геометрия. 7-9классы: учеб.для общеобразоват. учреждений / [Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.]. – 20 изд. – М. : Просвещение, 2010. – 384 с.
- Зиновкина М. М. Многоуровневое непрерывное креативное образование в школе // Концепт. – 2012. – № 9 (сентябрь). – ART 12116. – 1,0 п. л. – URL: http://www.covenok.ru/koncept/2012/12116.htm. – Гос. рег. Эл № ФС 77- 49965. – ISSN 2304-120X.
Chepizhenco Olesya Nikolaevna,
the teacher of mathematics of the Municipal comprehensive school №8, Kovrov, Vladimir region.
lesmi33@mail.ru
Summary. The elements of development of students' creativity at the Geometry lessons are shown in this article. The author describes a detailed plan of the lesson including all the stages of creative task system according to the innovative lesson structure, consisting of 8 blocks. The first unit provides the motivation of students to engage in work, the second block and sixth contain basic program material, the third block is emotionally – psychological relaxation. In the fourth section, students are asked a series of tasks, where early unknown facts students acquire when learning of real objects and are able to formulate the hypothesis. In the fifth section a system of training exercises to move from simple to complex is given. The seventh block is a computer-based intellectual support. And at last, the eighth block reflects feedback from students.
Keywords: creativity, school children, geometry, creativity, problem solving, development of interest in the subject.