Учителя математики и педагога не могут не интересовать вопросы формирования у школьников креативного мышления, нацеленности на создание творческого продукта, способности проявлять личностную позицию в конкретной научной, культурной сфере жизнедеятельности посредством объединения двух полюсов образования: культуры и жизни. Интересен и процесс формирования у учащихся системы когнитивно-процессуальных и личностных свойств, способных выработать смысловую позицию в отношении ценности научного знания, которая необходима для самореализации человека в современном мире. Исходя из того, что основная цель воспитания – научить человека творить себя как личность, необходимо выделить воспитывающий потенциал математического образования.
Педагогическая система преподавания математики в последнее время претерпела множество изменений и, как мне кажется, в лучшую сторону. Уроки, внеклассные мероприятия, кружки стали менять деятельность школьников. Трансляция готовых знаний и отработка определенных навыков сменилась деятельностным поисково-познавательным подходом. Поэтому и цели, и задачи на урок изменились. Претерпела изменения и сама структура урока и его наполнение. Так нами была использована структура креативного урока схемы целостной системы многоуровневого непрерывного креативного образования – НФТМ-ТРИЗ [1].
1. Блок мотивации. Познакомившись еще в дошкольном возрасте с различными геометрическими фигурами, вы уже тогда пытались выполнять над ними различные действия: из квадрата получать треугольники, собирать из треугольника, квадрата и прямоугольника домик, обклеивать коробочку с подарком для мамы цветной бумагой треугольной формы. Вы не знали свойств одинаковых фигур, не знали таких понятий как периметр и площадь, но достаточно сносно, на радость маме и воспитателю, выполняли все творческие задания, предлагаемые на занятиях. «Как мы это умудрялись делать?» – спросите вы. «Ведь нам это никто не рассказывал?». У вас уже в этом возрасте был достаточно большой жизненный опыт. Давайте и сегодня попробуем на него опереться.
В каких профессиях требуются знания площади фигуры? Это, конечно же, строители, агрономы, конструкторы и вы, если вы решили помочь своим родителям сделать ремонт в своей комнате – поклеить на стены новые обои [3]. Это довольно трудоемко, ведь нужно учесть много факторов, при этом купив обоев столько – сколько нужно: не переплатив за лишних 5 рулонов или не докупив полрулона. Дома вы должны будете выполнить мини-проект «Моя комната». Для этого вам нужно будет сделать все необходимые расчеты для своей комнаты и виртуально поклеить в ней обои. Сегодня нам с вами предстоит решить следующие задачи
- отрабатывать применение теоретических знаний на практике;
- формировать навык самостоятельного переноса и интеграции знаний как результат использования формул и схем;
- принимать решения в проблемной ситуации на основе переговоров.
- осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных ситуаций.
2. Блок творческого разогрева. Выяснив у ребят, куда клеят обои, и с чем у них ассоциируется слово «стена», предлагаю заполнить таблицу, опираясь на их уже имеющиеся знания. В левый столбец нужно записать предметы, на которые похож загаданный объект, а в правый – чем он от них отличается [4].
|
Стена |
|
|
На что похож? |
Чем отличается? |
|
Прямоугольник |
Геометрическая фигура |
|
Окно |
Меньше |
|
Батарея |
Холодная |
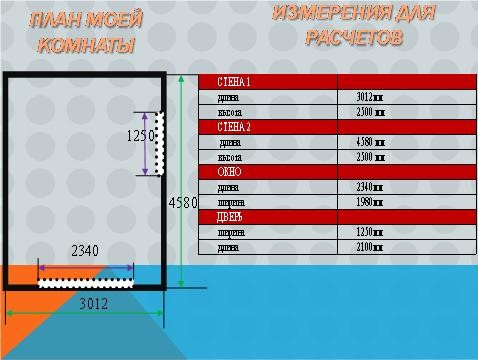
Делаем вывод, что стена похожа на геометрическую фигуру – прямоугольник, на ней есть окна, которые меньше по площади самой стены, и висят батареи, которые «греют» холодные стены.Далее ребятам предлагается рассмотреть план изображенной комнаты и предложенные измерения для расчетов.
Для более эффективной работы, для развития их творческого воображения, для однозначности представления таблицы с расчетами, ученики работают в группах, заполняя таблицу, в которой учитывают количество частей (участвующих в ремонте), составляющих объект (классная комната) [4].
|
Классная комната |
||
|
Части |
Сколько их? |
На что похожи? |
|
Стена |
4 |
На экран в кинотеатре |
|
Длина |
2 |
На плинтус |
|
Высота |
1 |
На трубу от батареи |
|
Окна |
3 |
На зеркала |
|
Двери |
1 |
На рот кита |
|
Батареи |
3 |
На гармошку |
3. Блок (психологическая разгрузка). Продолжая работать также в группах, ребята на этом этапе, представив себя строителями, измеряют: 1 группа – длины стен и высоту классной комнаты; 2 группа – длину и высоту окна; 3 группа – длину и высоту двери; 4 группа – длину и высоту радиаторов. Записывают результаты своих измерений.
4. Блок (головоломка). Ученики всех групп объединяются для построения схемы классной комнаты. Оказывается, что для наклеивания обоев нужно рассчитать площадь фигур различных форм, площадь фигур, у которых внутри или с краю часть вырезана, а бывает, что одну и ту же фигуру вырезают несколько раз. Итак, у нас возникла проблема: как это сделать?
На этом этапе учитель предлагает заготовленную головоломку «Квадраты». Перед вами четыре элемента. Чему равна площадь этих четырех фигур? Как ее найти? Попробуйте в группах выполнить задание.
Площадь каких фигур мы с вами уже умеем находить? Постарайтесь из данных фигур получить квадрат или прямоугольник. Молодцы! У нас получился квадрат, площадь которого мы уже умеем находить.
Что нужно знать для нахождения площади квадрата? Проведите в группах необходимые измерения и расчеты.
Итак, перед нами была проблема, решив которую мы познакомились с новым свойством площадей: площадь всей фигуры равна сумме площадей ее частей.
5. Блок (интеллектуальная разминка). Но для того, чтобы решить нашу проблему до конца, нам нужно познакомиться еще с одним важным свойством площадей.
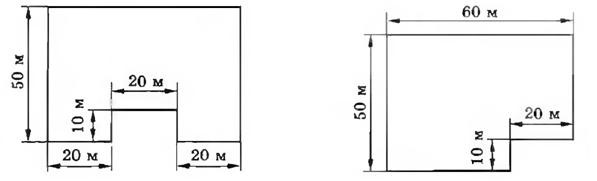
Для этого решим следующую задачу: на рисунке 4 изображены два огорода. На каждый ар нужно 4 кг удобрений. Сколько удобрений потребуется на каждый участок? На какой участок удобрений потребуется больше? [2]
Работу нужно выполнять в парах, предварительно также в парах заполнив таблицу «Я знаю – Я применю» для решения этой задачи. Напротив знания, которое нужно применить для решения данной задачи, нужно поставить плюс или галочку.
|
Я знаю |
Я применю |
|
1. понятие длины отрезка |
+ + - + - - - + - - + |
|
2. понятие площади |
|
|
3. понятие формулы |
|
|
4. формула площади прямоугольника |
|
|
5. формула площади квадрата |
|
|
6. формула периметра прямоугольника |
|
|
7. формула периметра квадрата |
|
|
8. свойства площадей фигур |
|
|
9 единицы измерения площадей |
|
|
10. перевод единиц измерения площадей |
|
|
11. свойства площадей равных фигур |
После решения этой задачи, ребята делают вывод, что площади равных фигур равны. На этапе интеллектуальной разминки могут быть использованы и учебные задачи открытого типа [4, 5].
6. Блок (содержательная часть). На этом этапе возвращаемся к схеме нашей классной комнаты, снова работаем в группах. Вычисляем по формуле нахождения площади прямоугольника площади окон, двери, радиаторов, стен. После этого вычисляем площадь той поверхности, которую нам нужно заклеить обоями. Высчитываем, какое количество рулонов нам нужно купить, если длина рулона 18 м, а ширина 1 м.
Ребята в группах заканчивают работу над проектом «Классная комната» и делают презентацию своего проекта.
После выполнения мини-проекта «Моя классная комната» в группах и всем классом вместе, ребята будут способны вполне самостоятельно провести виртуальный ремонт своей комнаты дома.
7. Блок (компьютерная интеллектуальная поддержка). Как вычислить площадь прямоугольника вы знаете. Как вычислить площади фигур, из которых вырезаны квадраты или прямоугольники – вы тоже знаете. А как все-таки найти площади неправильных фигур? Предложите способы вычисления и приведите свои примеры.
Пример 1. С помощью компьютерной программы на фигуру наложить сетку из одинаковых квадратиков, обработать фигуру. Но есть вероятность того, что точность измерения может быть нарушена.
Пример 2. Фигуру поместить в прямоугольную систему координат. Компьютерная программа зафиксирует координаты вершин фигуры и рассчитает длины сторон.
Этот мини-проект направлен на включение ребенка в процесс творчества средствами создания атмосферы радости поиска. Мини-проекты, связанные с явлениями, встречаемыми детьми в быту: ремонт квартиры (классной комнаты), при изучении темы «Площади и объемы» – вызывают у детей не только радость поиска, но и создают широкое положительное эмоциональное поле для дальнейшего постижения научных знаний по данному вопросу.
8. Блок (резюме). На последнем этапе учитель подводит краткие итоги урока, выявляет мнение об уроке, задают домашнее задание.
Вопросы для обратной взаимосвязи могут быть такими:
- Вам понравился сегодняшний урок (кому понравился – поднимите зеленые карточки, кому не понравился – красные).
- Расскажите самый запоминающийся момент урока.
- Сможете ли вы самостоятельно провести виртуальный ремонт своей комнаты?
Великий китайский мудрец Конфуций (около 551-479 лет до н.э.) две с половиной тысячи лет назад сказал: “Когда благородный муж учит и воспитывает, он ведет, но не тянет за собой, побуждает, но не заставляет, указывает путь, но позволяет ученику идти самому. Поскольку он ведет, а не тянет, он пребывает в согласии с учеником. Поскольку он побуждает, а не заставляет, учеба дается ученикам легко. Поскольку он лишь только открывает путь, он предоставляет ученику возможность размышлять”. Такая позиция очень близка современному учителю и современным детям.
Ссылки на источники
- Зиновкина М. М. Многоуровневое непрерывное креативное образование в школе // Концепт. – 2012. – № 9 (сентябрь). – ART 12116. – 1,0 п. л. – URL: http://www.covenok.ru/koncept/2012/12116.htm. – Гос. рег. Эл № ФС 77- 49965. – ISSN 2304-120X.
- Математика: Учеб. для 5 кл. общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 17-е изд., перераб. – М.: Мнемозина, 2005. – 280 с.: ил.
- Развитие компетентности учителя современной гимназии. Практико-ориентированное пособие. Авторы составители: Л.М. Бурнашева, Т.Н. Харламова, П.Л. Зайцев, В.Д. Евсюкова, Л.К. Нефедова, Н.А. Зубачевская, Р.Р. Сабирова, Л.Г. Соколина, Н.И. Дорошенко, Л.П. Звягинцева, Ю.А. Нацкевич, С.Л. Попова, М.В. Чернуцкая, Т.В. Свенч. – Омск: Управление образования администрации города Омска 2004г, 135с.
- Горев П.М., Утемов В.В. Путешествие в страну творчества: учебно-методическое пособие. – Киров: Изд-во ВятГГУ, 2012. – 144 с., ил.
- Утёмов В. В. Задачи открытого типа как средство развития креативности учащихся средней школы // Концепт: научно-методический электронный журнал официального сайта эвристических олимпиад «Совёнок» и «Прорыв». – 4 квартал 2011, ART 11-4-02. – Киров, 2011 г. – URL: http://www.covenok.ru/koncept/2011/11402.htm. – Гос. рег. Эл № ФС 77-46214. – ISSN 2225-1618.
Titovа Maria,
mathematics teacher of MKOU "Nizhneirtyshsky SOSh" of the Sargatsky municipal region of the Omsk region, Omsk
titova_masha@mail.ru
Development of a creative lesson in the 5th class on the subject «Areas of Figures»
Abstract. Development of a creative lesson of the subject «Areas of Figures» is presented in article. The author according to structure of a creative lesson in innovative pedagogical system НФТМш developed all blocks of a lesson. The solution of creative tasks according to the chosen subject is considered.
Keywords: creative tasks, area of figures, creative imagination, positive emotional field.