При изучении многих дисциплин в учебном заведении любого уровня используются задачи – специально вымышленные ситуации, используемые для изучения и закрепления знаний, умений и навыков. Для каждой темы задачи решаются в системе: сначала решаются обучающие задачи, целью которых является формирование теоретических знаний и связанных с ними умений. При этом типовые задачи решаются по алгоритму, такой способ решения не требует творческой активности мышления. Затем решаются задачи, для закрепления и контроля знаний и умений. При алгоритмизированном решении задач учащиеся учатся анализу при знакомстве с основными элементами задачи, системному видению проблемы: определяют связи между компонентами и требуемым результатом. Однако, в этих условиях аналитико-синтетические свойства мышления учащихся проявляются на воспроизводящем уровне. Система решаемых задач обеспечивает, а точнее, обрекает педагога и учащегося на субъект-объектное взаимодействие. Такой стиль взаимодействия не удовлетворяет требования современного общества. Поэтому педагоги выбирают для использования в своей практике эвристические, творческие задачи. Но как определить, является ли задача творческой? Для поиска ответа на этот вопрос мы обратились к работе ученых М. М. Зиновкиной, Р. Т. Гареева, П. М. Горева, В. В. Утемова [1, с. 59], которые, анализируя творческие задачи для определения их возможностей развития креативности учащегося, пришли к мнению классифицировать задачи на закрытые и открытые. Используя типизацию задач частично открытого типа выше названных авторов, мы пришли к выводу, что в школьной практике на уроках черчения возможно активно использовать такие задачи для развития творческих способностей учащихся.
Задача частично открытого типа «Бочки и ящики» (рис. 1) решается на уроке черчения при изучении проецирования на одну плоскость проекций, её дидактический потенциал в том, что при её решении учащиеся преодолевают психологический барьер, развивают пространственное воображение. Кроме того, в оригинальной форме закрепляется информация, которую надо запомнить.
Эта задача открывает целую серию задач частично открытого типа, называемые «Пробки». Автор [2, с. 109] дает исходную задачу в виде изображения трех отверстий, по условию требуется подобрать форму пробки, которая могла бы поочередно закрывать все три отверстия (рис. 2).
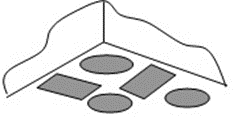
Рис. 1. Задача «Бочки и ящики»
В углу двора стояли бочки и ящики, причем все объекты стояли на земле (рис. 1). После дождя их убрали, на земле остались сухие места. Ответьте на вопросы:
- Сколько было бочек и ящиков?
- Что назовем плоскостью проекций, проецирующими лучами, проецируемым предметом, проекцией?
- Проецирование будет центральным или параллельным?
- При каком условии погоды проецирование будет косоугольным, прямоугольным?
При попытке решения задачи, представленной на рисунке 2 оказалось, что затруднительна для решения ввиду имеющихся у учащихся психологических барьеров и малого опыта мысленного создания пространственных образов и, в частности, мысленного формообразования.
Рис. 2. Задача «Пробки»
Не смотря на заданные три характеристики формы объекта, эту задачу следует отнести к задачам, решаемым в недрах творческого воображения, так как учащиеся в школе не изучают сечения геометрических тел, необходимые для создания искомого образа формы объекта. Поэтому появилась необходимость создания системы задач, (таблица 1) целью которой является создание условий для проживания учащихся в условиях необходимости использования аналитико-синтетических характеристик процессов воображения. «Процессы воображения состоят в мыслительном разложении исходных представлений на составные части (анализ) и последующем их соединении в новых сочетаниях (синтез)», – именно эти процессы воображения, которые описывает П. И. Пидкасистый [3, с. 246], учитывались при создании дидактической системы творческих задач. Её рекомендуется использовать при изучении проецирования на одну, две и три плоскости проекций. Как показала практика, только реализация системы задач дает положительный результат решения задач такого содержания.
При изучении черчения следует помнить о том, что образ «рождается» под влиянием двух взаимосвязанных детерминант: 1) наглядной основы, в данном случае изображения отверстий на общем фоне и 2) требований к действиям или установкой, условием задачи.
Задача «Бочки и ящики» решается учащимися легко по причине известности ситуации – наглядная основа понятна, все видели когда-то, как шел дождь и что под предметами остается сухое место, например, под автомобилем. Этот жизненный опыт помогает решить задачу, использовать имеющуюся информацию в новых условиях – конкретную ситуацию из жизни необходимо пояснить с использованием специфических понятий.
Задача «Пробки», данная в варианте как на рис. 2 без предварительной подготовки является для учащихся тупиковой, практика показала, что требования условия задачи для учащихся не реализуемы по причинам, описанным выше.
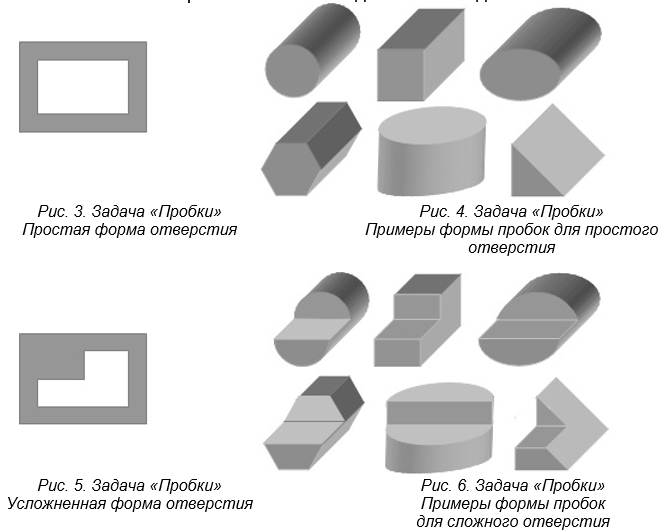
При изучении проецирования на одну плоскость проекций решается задача, изображенная на рисунке 3, её можно задавать и на дом. Необходимо нарисовать форму пробки, проходящей через отверстие прямоугольной формы. Полученные результаты, оказываются для учащихся неожиданными: ответов может быть очень много (рис. 4). После этого задается задача с усложненной формой отверстия (рис. 5), догадка о необходимости преобразовать форму имеющихся пробок приходит быстро. Преобразование формы пробок состоит в том, что необходимо вырезать их часть, таким образом «подогнать» форму пробки под заданную форму отверстия (рис. 6). Этот промежуточный вариант условия задачи очень важен тем, что кроме осознания многовариантности ответов, усваивается путь решения задачи преобразованием форм объектов. Это очень важный момент в получении нового опыта решения внешне однотипных задач.
Решение следующих задач требует от учащихся включения активного воображения, оперирования единицами конкретной информации о форме объекта и его проекциях для создания новых оригинальных связей между ними. В условии этих задач задаются изображения двух отверстий (рис. 7), задающих форму пробки, которая может поочередно закрывать оба отверстия.
Следует согласиться, что эта задача не относится к задачам открытого типа. Но в системе она имеет свою дидактическую функцию: объектом необходимо мысленно манипулировать в пространстве, изменяя его положение относительно отверстий, чтобы «увидеть» её качество закрывать отверстие или проходить через него. Конечно, задача решается без сопровождения особыми эмоциями, однако, ее дидактическая функция не удивлять, а дать дополнительный познавательный опыт для подготовки к решению следующей задачи.
Теперь пришло время решать заключительную задачу (рис. 8).
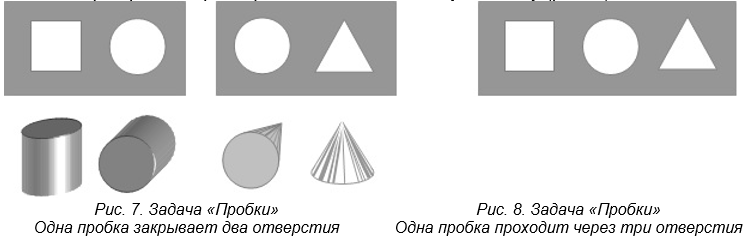
При анализе её графического условия оказывается, что оно состоит из элементов условий предыдущих двух задач: отверстия имеют квадратную, треугольную форму и форму круга. Однако форма пробок, используемых в предыдущих задачах, не подходят к новому условию. Ни манипуляции формой пробок в пространстве, ни попытки вырезать часть каждой из них, что приводило к успеху при решении предыдущих задач, при решении данной задачи не дает правильного ответа. Хотя при обсуждении ситуации звучат мнения учащихся о том, что с формой простого геометрического тела что-то надо делать: или вырезать, отрезать, или добавлять элементы. Ментально решить задачу не удаётся. На вопрос о том, какой из геометрических тел необходимо оставить для дальнейшего решения задачи, выбор делается в пользу цилиндра. Он более перспективен для преобразований в соответствии с условием задачи: от него возможно удалить часть, чтобы получилась искомая форма. А какую по форме часть необходимо удалить от формы цилиндра мысленно или с использованием рисунков-набросков решить трудно.
В этом случае прибегаем к быстрому моделированию формы из пластилина. Как только у учащегося в руках оказывается стека (деревянная лопаточка для работы с пластилином) и цилиндрическая заготовка, достаточно поманипулировать стекой чтобы догадаться какой формы части цилиндра необходимо отсечь.
Почему необходима работа с предметами в руках для представления формы объекта? Ответ на вопрос находим у Н. Д Бондаревой [4, с. 48], которая на основании анализа большого количества источников делает вывод о том, что умственные действия с пространственным образом формируется поэтапно. Сначала необходимы практические действия с реальным предметом, которые на следующем этапе заменяются имитирующими движениями. Только после этого возникают умственные действия с представлениями.
Согласимся с тем, что учащиеся получали опыт моделирования объектов в начальной школе. Однако спонтанно учащиеся не могут применить этот опыт, необходимо организовать экскурс в соответствующие блоки памяти. Трудно переоценить значение полученного учащимися опыта для дальнейшей работы воображения при решении творческих задач на уроках черчения.
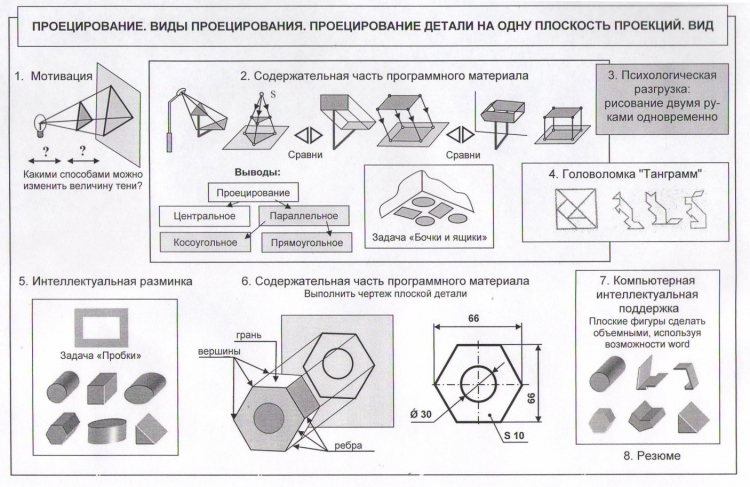
На рисунке 9 информационно-графическим блоком представлен двух часовой урок на тему «Проецирование. Виды проецирования. Проецирование на одну плоскость проекций». Здесь использованы две задачи из упомянутых в рассматриваемой системе задач. Остальные задачи найдут свое применение при изучении проецирования на две и три плоскости проекций.
Таблица 1
|
Анализ системы задач частично открытого типа, используемых на уроках черчения в процессе изучения темы «Проецирование на плоскости проекций»
|
Наглядная основа условия задачи
|
Установка условия задачи
|
Дидактическая функция задачи
в системе
|
Соответствие критериям задач
частично открытого типа
|
|
Задача «Бочки, ящики»
|
В углу двора стояли бочки и ящики, причем все объекты стояли на земле (рис. 1). После дождя их убрали, на земле остались сухие места. Ответьте на вопросы:
- Сколько было бочек и ящиков?
- Что назовем плоскостью проекций, проецирующими лучами, проецируемым предметом, проекцией?
- Проецирование будет центральным или параллельным?
- При каком условии погоды проецирование будет косоугольным, прямоугольным?
|
Задача способствует:
- преодолению психологического барьера;
- развитию пространственного воображения.
Создает условия для:
- запоминания информации в оригинальной форме;
- использования имеющейся информации в новых условиях (конкретная ситуация из жизни поясняется с использованием специфических понятий).
|
Закрытый характер условия и решения (понятно, что и как искать, но ответ не единственный).
Условие можно интерпретировать неоднозначно, следствием чего является многозначность ответа.
Информации для решения достаточно.
Способ решения – по проекции определить форму объекта – не известен
|
|

Задача «Пробки»
Простая форма отверстия
|
Задача выполняется дома или в классе.
Нарисовать форму пробки для отверстия прямоугольной формы.

|
Задача способствует:
- преодолению психологического барьера;
- развитию пространственного воображения, интуиции;
- знакомству с контурами проекций (габаритных прямоугольников) разных геометрических тел;
|
Закрытый характер условия и решения (понятно, что и как искать, но ответ не единственный).
Информации для решения достаточно. Способ решения заключается в мысленном представлении формы пробки, подходящей форме отверстия.
|
|

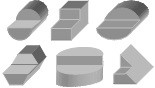
Задача «Пробки»
Усложненная форма
отверстия
|
Нарисовать форму пробки для отверстия заданной формы.
|
Задача способствует:
- преодолению психологического барьера;
- развитию пространственного воображения, интуиции;
- знакомству с контурами проекций геометрических тел с вырезами;
|
Закрытый характер условия и решения (понятно, что и как искать, но ответ не единственный).
Информации для решения достаточно. Способ решения заключается в мысленном представлении формы пробки, соответствующей форме отверстия, что является познавательным затруднением из-за недостатка опыта декодирования информации о форме объекта по имеющимся проекциям.
|
|

Задача «Пробки»
Одна пробка закрывает
два отверстия
|
Нарисовать форму пробки, которая может поочередно закрывать оба отверстия

|
Задача способствует:
- преодолению психологического барьера;
- развитию пространственного воображения, интуиции;
- предварительному изучению проекций геометрических тел способом мысленных манипуляций объектом
|
Закрытый характер условия – понятно, что искать, закрытый характер ответа – понятно, что получить. Ситуация познавательного затруднения из-за недостатка опыта декодирования информации о форме объекта по имеющимся проекциям.
|
|

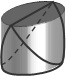
Задача «Пробки»
Одна пробка закрывает
три отверстия
|
Нарисовать форму пробки, которая может поочередно закрывать три отверстия
|
Задача способствует:
- преодолению психологического барьера;
- развитию пространственного воображения, интуиции.
Требуется использование предметного моделирования формы из пластических материалов или манипулировать стекой – средством изменения формы цилиндра
|
Закрытый характер условия – понятно, что искать, закрытый характер ответа – понятно, что получить. Ситуация познавательного затруднения из-за недостатка опыта декодирования информации о форме геометрического тела с сечениями по имеющимся изображениям проекций. Проекции расположены не по стандартным правилам.
|
|
Танграмм-головоломка

|
Составить из элементов танграмма сюжетные картинки

|
Задача способствует:
- преодолению психологического барьера;
- развитию пространственного воображения, интуиции;
- развитию фантазии
|
Открытый характер условия – непонятно, что искать, открытый характер ответа – получить можно много вариантов ответа.
|
|
Рисунок 9.
|
Проецирование детали на три плоскости проекций. Три вида.
Ссылки на источники
- Зиновкина М. М., Гареев Р. Т., Горев П. М., Утемов В. В. Научное творчество: инновационные методы в системе многоуровневого непрерывного креативного образования НФТМ-ТРИЗ: учебное пособие. Киров: Изд-во ВятГГУ, 2013. – 109 с.
- Воротников И. А. Занимательное черчение. Пособие для учащихся. Изд. 3-е, доп. и перераб. М., Просвещение, 1977. – 192 с.
- Психология и педагогика: учебник для вузов / под ред. П. И. Пидкасистого. – М.: Издательство Юрайт; Высшее образование, 2010. – 714 с.
- Бондарева Н. Д. Развитие пространственных представлений младших школьников в процессе графической деятельности и конструирования: Дис…к.п. наук: 13.00.02. – М. 2005. – 2 с.: ил.
Rushaniya Minachova,
candidate of pedagogical science, docent of social, humanitarian and economic subjects department, South-Russian State Polytechnic University named after M.I. Platov, Kamensk-Shakhtinsky affiliation.
minach-han2008@yandex.ru
Solving creative problems in school practice while learning how to project an object onto the projections surfaces
Abstract. The conditions necessary for ensuring successful solution of the creative tasks connected directly with the study of the topic «Projection of objects on the level of prospectives» are considered in the article. One of the conditions is the system of tasks, presented by the author, solving them at the lessons and at home a student runs through the framework of necessity to use analytic-synthetical characteristics of the imagination processes creating the images of objects. The second condition is application of materialistic modeling of an object of a hypothesized shape according to the given draft.
Key words: a creative task, an image, shape transformation, tasks of a partly open type, form and tasks analysis.