Развитие креативных способностей учащихся на уроках математики

 

Необходимость развития личности с широким интеллектуальным потенциалом, способствующим развитию креативности как основы инновационной деятельности, отражена в федеральных и региональных документах, например, в Федеральном государственном образовательном стандарте основного общего образования, утверждённом приказом № 1897 Министерства образования и науки Российской Федерации 17 декабря 2010 г. [1], указах, постановлениях, распоряжениях и иных нормативно-правовых актах по школьному образованию.

Система образования в целом направлена на развитие созидающего творческого воображения, а не фантазирования, что было бы существенней для развития личности. Поэтому имеющиеся у большинства людей задатки к фантазированию в процессе обучения зачастую гасятся. Многим это не вредит, но тем, кто попадает в творческую среду, на научную, инженерную или изобретательскую работу, часто приходится перестраиваться уже в зрелом возрасте. Огромную помощь в этом может оказать методика развития творческого воображения и фантазирования.

«Креативность», «творческий подход», «креативная личность», «творческие успехи», «думать творчески», «проявление креативности» – эти понятия в современном обществе являются показателями профессионализма. Ведь именно креативность, способность к творчеству и созиданию, мы считаем атрибутом одарённости, таланта, гения.

Чтобы у школьника развивалось творческое мышление, необходимо, чтобы он почувствовал удивление и любопытство, повторил путь человечества в познании, удовлетворил с аппетитом возникшие потребности в записях. Только через преодоление трудностей, решение проблем, ребенок может войти в мир творчества. А в наше время только творческий человек, нестандартно мыслящий, может достичь успеха.

Креативность – это процесс дивергентного мышления, где под дивергентным мышлением понимается не направленное мышление, а способность мыслить вширь, т. е. видения различных сторон изучаемого объекта; умение мыслить «в разных направлениях».

Развитие креативности способствует решению следующих задач:

Развитию креативности на уроках математики способствует применение следующих задач: вариативные задачи, найди «лишнее» число, логические цепочки, магические квадраты, «найди ошибку», задачи на разрезание многоугольников, решение головоломок, ребусов, занимательных задач, задач на смекалку и софизмов, задачи на перебор вариантов, танграм, оригами.

При выполнении таких задач учащимся чаще всего приходится пользоваться методом проб и ошибок, что, в конечном счете, развивает интуицию, творчество, способность искать другой способ решения, отказавшись от ложного пути. Поиск решения таких задач воспитывает усидчивость, развивает различные виды памяти, внимание.

1. Вариативные задачи. Одним из средств организации творческого подхода на уроках математики может стать преобразование задачи.

Задача. «Из пункта А в пункт В, расстояние между которыми 18 км, навстречу друг другу вышли два пешехода. Скорость одного пешехода 2 км/ч, а скорость другого – 4 км/ч. Какое расстояние будет между пешеходами через 2 часа?».

После её решения предложить учащимся снять условие, что пешеходы идут навстречу друг другу. Изменится ли решение? Каким образом? Возникает новая ситуация – пешеходы идут в одном направлении.

В каком именно? Возможны два случая. А может быть пешеходы идут в разных направлениях? Ещё одна задачная ситуация. В итоге имеем несколько задач.

Можно убрать другое условие – расстояние между пунктами 18 км. Получим такую задачу: «Из пунктов А и В навстречу друг другу вышли два пешехода. Скорость одного пешехода 2 км/ч, а скорость другого – 4 км/ч. Какое расстояние будет между ними через 2 ч.? » Невозможно решить её, не зная расстояние S между пунктами. Но ведь оно может быть разным. Каким? С каким значением будем сравнивать S? С пройденным пешеходами расстоянием, равным (2+4)*2=12 км. Возможны две ситуации: 1) S>12; 2) S<12.

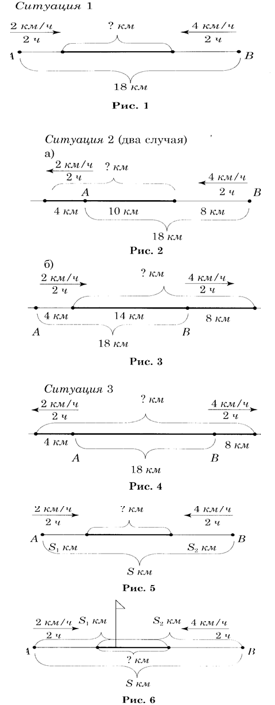
Это ли не мыслительная деятельность? Здесь и перебор вариантов, и определение дополнительных условий, и формулировка новой задачи, и абстрагирование, и открытие общего способа решения задач определённого типа. В данном случае снятие условия в стандартной задаче приводит к вариативной задаче. Основной характеристикой последней является неоднозначное расположение объектов, включённых в условие, что ведёт к необходимости рассмотрения нескольких ситуаций [2].
2. Зачеркните «лишнее» число.

а) 12, 45, 678, 94, 3456

б) 25, 16, 100, 81, 50, 9

в) 35, 72, 8463, 127, 69
3. Логические цепочки (заметить закономерность в рядах чисел, дописать в каждую строчку по два следующих числа).

а) 3, 7, 11, 15, 19, 23, …

б) 2, 4, 6, 9, 11, 14, 16, …

в) 4, 7, 10, 13, 16, 19, …
4. Упражнение на поиск общих признаков объектов и построение определения на основе сравнения. Сравните понятие последовательности и функции. Напишите все общие признаки и различия. Оформите в виде таблицы. На основе полученных данных постройте определение последовательности. Выделите, какое понятие является родовым. Изобразите взаимосвязь этих понятий.

 

Общие признаки понятий	Различные признаки
Существуют два множества Между множествами есть взаимно однознач­ное соответствие. Можно задать графически Можно задать формулой И т. д 1.   Одно из множеств представляет собой мно­жество натуральных чисел. 2.   График состоит из множества точек, которые нельзя соединить одной линией. 3.   И т. д

 

На основе сравнения делаем вывод, что последовательность – это частный вид функции, что понятие функции является родовым.
5. Упражнение на построение причинно-следственных цепочек. Из списка предложений выберите несколько троек предложений так, чтобы каждое последующее следовало из предыдущего.

а) Дана арифметическая прогрессия (а_п) :-3; 1; 5 ;8; …

б) log₅ 25 = 5, так как 5∙5 = 25

7.  Задачи на разрезание многоугольников (используются на олимпиадах по математике различного уровня).

1) Разрежьте прямоугольник (рис. 8), длина которого равна 9 см, а ширина 4 см, на две равные части так, чтобы из них можно было сложить квадрат.

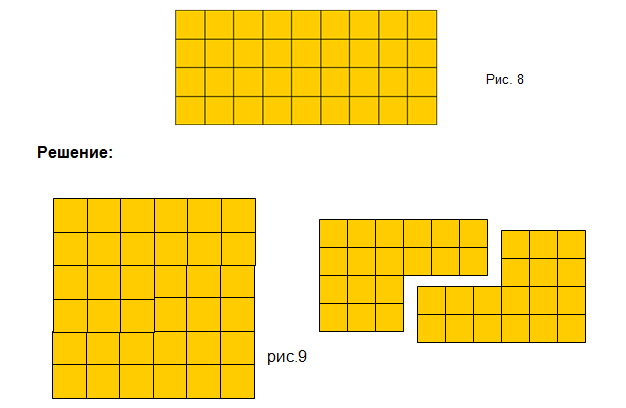
2) Разрежьте фигуру на четыре равные части и сложите из этих частей квадрат с квадратным отверстием посередине (Рис.10).

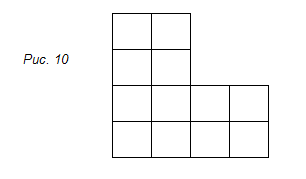
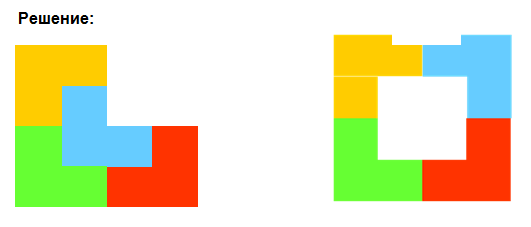
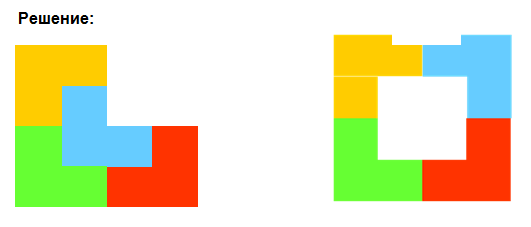
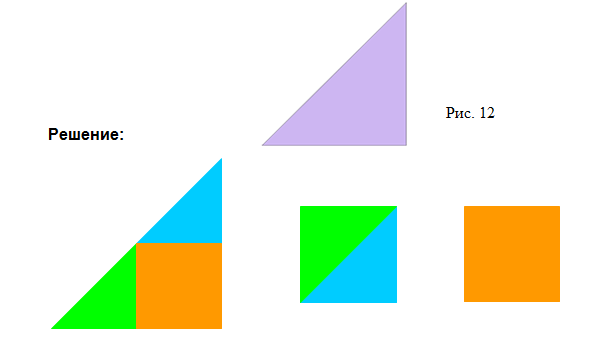
3) Разрежьте данный треугольник на три неравные части, из которых можно было бы составить два равных квадрата (Рис. 12).

Решение задач-головоломок, ребусов, занимательных задач, задач на смекалку и софизмов также способствует развитию креативности.

Софизмы по теме «Логарифмы» и «Площади»:

1) У бабушки в деревне есть несколько птиц. Все они, кроме двух, – утки, все, кроме двух,– цыплята, и все, кроме двух,– гуси. Сколько птиц у бабушки?

2) 7 карасей тяжелее, чем 3 окуня. Что тяжелее – 5 карасей или 2 окуня?

1) В мастерской Деда Мороза есть 4 различные краски и 3 вида блёсток для изготовления новогодних шаров. Сколькими способами можно покрасить шарик?

2) В магазине продаются 5 разных больших мяча, 3 разных средних мяча, и 4 вида маленьких. Сколькими способами можно купить комплект «большой+ средний+маленький».

3) В комнате живут 5 девочек. Сколько различных графиков дежурств можно составить на неделю, если каждый день дежурит один человек?

Применять различные средства и методы обучения для формирования креативности необходимо как на уроках, так и во внеурочной деятельности учащихся.

На внеклассных занятиях из раздела наглядная геометрия рассматривается решение интересных головоломок, занимательных задач, бумажных геометрических игр. Такие задания помогают развивать у ребят смекалку, находчивость при решении задач и творческое мышление.

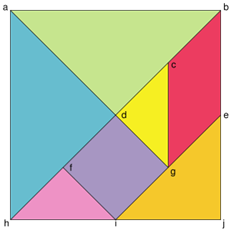
Как творчески можно разнообразить урок геометрии? Например, используя танграм. Конструируя, мы запоминаем названия геометрических фигур, их свойства, отличительные признаки, обследуем формы зрительным и осязательно-двигательным путем, свободно перемещаем их с целью получения новой фигуры. У нас развивается умение анализировать простые изображения, выделять в них и в окружающих предметах геометрические формы, практически видоизменять фигуры путем разрезания и составлять их из частей.

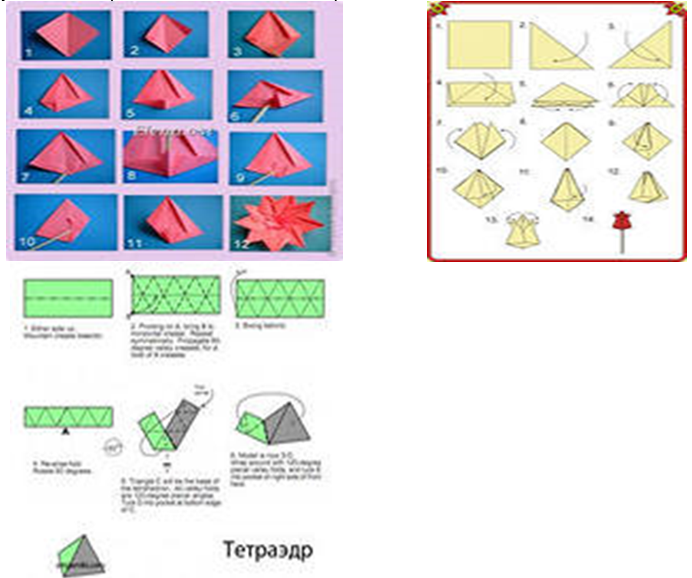
Или используя оригами. Оригами развивает творческое, комбинированное и пространственное мышление, чувство формы. Искусство оригами является не только увлекательным способом проведения досуга, но и средством решения многих педагогических задач, в частности развития мелкой моторики. Совершенствуя и координируя движение пальцев и кистей рук, оригами влияет на общее интеллектуальное развитие ребёнка, в том числе и на развитие речи. Ведь ещё В. А. Сухомлинский сказал: «Истоки творческих способностей и дарования детей на кончиках их пальцев. От пальцев, образно говоря, идут тончайшие ручейки, которые питают источник творческой мысли».

Заключение. Обучение и познание – сложные процессы, они предполагают, прежде всего, деятельность учителя и деятельность учащегося. Поэтому учитель даёт не только научную информацию по своему предмету, но и планирует, организует, контролирует учебную деятельность ученика, развивает навыки учебного труда, мышление (в том числе и креативное), способности, умения применять знания на практике – всё то, что поможет учащемуся добиться успеха на своем жизненном пути, ведь на протяжении всей жизни человек может и должен развивать имеющееся у него творческое начало [3].

Сегодня все более очевидным становится тот факт, что социальный прогресс во многом зависит от того, какое количество творческих людей способны его осуществлять. Именно от степени развитости в человеке творческого начала зависит развитие науки и техники.

Человек с творческим типом мышления быстрее адаптируется к различным условиям жизни, находит нестандартные решения любых возникающих проблем, способен адекватно оценивать свои результаты и, совершив ошибки на своем творческом пути, способен к их исправлению.

 

bardanova.vera@mail.ru

latialla@mail.ru

liland-80@mail.ru

raimova77gim@mail.ru

galiah1956@mail.ru

Abstract. The article discusses various tasks, promoting development of creative thinking in mathematics lessons and after school.

Key words: problems of open type, creative tasks, tasks of cutting, sophisms, variational problems, problem with multiple solutions, the development of creativity, creative potential.