Введение. Неуспеваемость по математике является одной современных проблем, затрагивающая деятельность многих специалистов: врачей, психологов, учителей, социологов, политологов и т. д. Несмотря на сложность рассматриваемой проблемы, зачастую решать ее приходится только одному учителю математики.
Общие рекомендации по работе с неуспевающими учащимися не дают желаемого результата, поскольку построены на принципах догматического обучения. В условиях личностно-ориентированного обучения на первый план выходит личность ребёнка, особенности его восприятия мира и себя в нем.
Специалисты по проблеме школьной неуспеваемости «среди неуспевающих школьников выделяют определенную категорию детей, которые характеризуются отсутствием необходимого уровня познавательной активности. Л. С. Славина назвала детей, отличающихся этой особенностью, «интеллектуально пассивными». Интеллектуально пассивные школьники отличаются нормальным интеллектуальным развитием, которое легко обнаруживается в игре и практической деятельности. Однако в учении они производят впечатление крайне неспособных, даже иногда умственно отсталых, так как не могут справиться с самыми элементарными учебными заданиями» [5, с.120].
Тесно с ней связана и проблема психологической инерции, под которой понимают предрасположенность к какому-либо конкретному методу и образу мышления, игнорирование всех возможностей, кроме единственной, встретившейся в самом начале. Психологическая инерция – привычка к стандартным действиям в типовых ситуациях или упорное стремление человека думать и действовать в соответствии с выработанными и приобретенными привычками и представлениями [1].
Так, например, среди неуспевающих учащихся часто возникают ошибки такого плана: смешивают правила умножения степеней с правилом возведения в степень (5x2·6x3=30x6); неправильно применяют формулы ((а+b)2=a2+b2)
Негативные психологические установки, вызывающие инерцию мышления при изучении математики, можно сформулировать следующим образом: «Есть только один путь решения задачи», «Учитель (мама, папа, друг, сосед) сказал», «Не может быть в задаче два решения», «Так все делают», «Такого не может быть, потому что «это» не видно» и т. д.
Основные положения методики работы.
Исходная позиция педагога – каждый ребенок талантлив от природы.
Принцип работы педагога – воспитание личности учащегося через включение его в совместное творчество.
Задача педагога – создать педагогические условия для выявления творческих способностей учащихся и их развития в процессе математического образования.
Подцелями системы НФТМ является формирование в учебном процессе прежде всего дивергентного мышления и воспитания креативных качеств личности [7; 8].
Система заданий. Важнейшим элементом структуры учебной деятельности является учебная задача, решая которую учащийся выполняет определенные учебные действия и операции. Характеристика творческих задач: данных для решения недостаточно или их избыток, данные противоречивы или недостоверны, дается ситуация, а задачу еще надо поставить, решение вероятностное и множественное; ответ непредсказуем.
Противоречие в условии задачи – главное требование к открытой задаче.
Достаточность условия – второе требование к открытым задачам.
Корректность вопроса также необходимое требование к формулировке открытых задач.
Таким образом, в работах [2; 7; 8] выявлены три основных требования к формулировке задачи открытого типа:
– наличие внутреннего противоречия в условии задачи: главной движущей силой процесса обучения являются противоречия;
– достаточность условия: условие задачи должно содержать все необходимые данные для ее решения;
– корректность постановки вопроса: учащийся не должен испытывать трудностей с правильной интерпретацией вопроса к задаче.
В. Н. Клепников предлагает условно разделить задачи, способствующие развитию творческого мышления, на несколько типов: необычные, софистические, парадоксальные, конструктивные, открытые.
I. Необычные задачи – это задачи, которые на первом этапе осмысления противоречат «здравому смыслу», непривычные для восприятия [4, с. 46].
II. Софистические задачи – это задачи, в которых сознательно «спрятана» ошибка, которую нужно распознать [4, с. 47].
III. Конструкторские задачи – это задачи, для решения которых нужно произвести геометрические, пространственные, топологические преобразования или построить в своём воображении адекватную и эффективную модель решения задачи.
IV. Парадоксальные задачи – это задачи, которые дают возможность разрешить противоречие между единым и многим, конечным и бесконечным, частью и целым, статикой и динамикой, закономерным и случайным, рациональным и иррациональным, предсказуемым и непредсказуемым.
V. Открытые задачи – это задачи, которые всегда имеют несколько путей решения и могут иметь несколько возможных равноценных ответов.
Примеры заданий, способствующих развитию творческого мышления учащихся при изучении темы «Площадь».
Пример 1. Дан треугольник со сторонами а, b, c. Вывести формулы для нахождения площади произвольного треугольника.
Общие рекомендации по работе с неуспевающими учащимися не дают желаемого результата, поскольку построены на принципах догматического обучения. В условиях личностно-ориентированного обучения на первый план выходит личность ребёнка, особенности его восприятия мира и себя в нем.
Специалисты по проблеме школьной неуспеваемости «среди неуспевающих школьников выделяют определенную категорию детей, которые характеризуются отсутствием необходимого уровня познавательной активности. Л. С. Славина назвала детей, отличающихся этой особенностью, «интеллектуально пассивными». Интеллектуально пассивные школьники отличаются нормальным интеллектуальным развитием, которое легко обнаруживается в игре и практической деятельности. Однако в учении они производят впечатление крайне неспособных, даже иногда умственно отсталых, так как не могут справиться с самыми элементарными учебными заданиями» [5, с.120].
Тесно с ней связана и проблема психологической инерции, под которой понимают предрасположенность к какому-либо конкретному методу и образу мышления, игнорирование всех возможностей, кроме единственной, встретившейся в самом начале. Психологическая инерция – привычка к стандартным действиям в типовых ситуациях или упорное стремление человека думать и действовать в соответствии с выработанными и приобретенными привычками и представлениями [1].
Так, например, среди неуспевающих учащихся часто возникают ошибки такого плана: смешивают правила умножения степеней с правилом возведения в степень (5x2·6x3=30x6); неправильно применяют формулы ((а+b)2=a2+b2)
Негативные психологические установки, вызывающие инерцию мышления при изучении математики, можно сформулировать следующим образом: «Есть только один путь решения задачи», «Учитель (мама, папа, друг, сосед) сказал», «Не может быть в задаче два решения», «Так все делают», «Такого не может быть, потому что «это» не видно» и т. д.
Основные положения методики работы.
Исходная позиция педагога – каждый ребенок талантлив от природы.
Принцип работы педагога – воспитание личности учащегося через включение его в совместное творчество.
Задача педагога – создать педагогические условия для выявления творческих способностей учащихся и их развития в процессе математического образования.
Подцелями системы НФТМ является формирование в учебном процессе прежде всего дивергентного мышления и воспитания креативных качеств личности [7; 8].
Система заданий. Важнейшим элементом структуры учебной деятельности является учебная задача, решая которую учащийся выполняет определенные учебные действия и операции. Характеристика творческих задач: данных для решения недостаточно или их избыток, данные противоречивы или недостоверны, дается ситуация, а задачу еще надо поставить, решение вероятностное и множественное; ответ непредсказуем.
Противоречие в условии задачи – главное требование к открытой задаче.
Достаточность условия – второе требование к открытым задачам.
Корректность вопроса также необходимое требование к формулировке открытых задач.
Таким образом, в работах [2; 7; 8] выявлены три основных требования к формулировке задачи открытого типа:
– наличие внутреннего противоречия в условии задачи: главной движущей силой процесса обучения являются противоречия;
– достаточность условия: условие задачи должно содержать все необходимые данные для ее решения;
– корректность постановки вопроса: учащийся не должен испытывать трудностей с правильной интерпретацией вопроса к задаче.
В. Н. Клепников предлагает условно разделить задачи, способствующие развитию творческого мышления, на несколько типов: необычные, софистические, парадоксальные, конструктивные, открытые.
I. Необычные задачи – это задачи, которые на первом этапе осмысления противоречат «здравому смыслу», непривычные для восприятия [4, с. 46].
II. Софистические задачи – это задачи, в которых сознательно «спрятана» ошибка, которую нужно распознать [4, с. 47].
III. Конструкторские задачи – это задачи, для решения которых нужно произвести геометрические, пространственные, топологические преобразования или построить в своём воображении адекватную и эффективную модель решения задачи.
IV. Парадоксальные задачи – это задачи, которые дают возможность разрешить противоречие между единым и многим, конечным и бесконечным, частью и целым, статикой и динамикой, закономерным и случайным, рациональным и иррациональным, предсказуемым и непредсказуемым.
V. Открытые задачи – это задачи, которые всегда имеют несколько путей решения и могут иметь несколько возможных равноценных ответов.
Примеры заданий, способствующих развитию творческого мышления учащихся при изучении темы «Площадь».
Пример 1. Дан треугольник со сторонами а, b, c. Вывести формулы для нахождения площади произвольного треугольника.
Структура дополнительных занятий для учащихся 8 классов.
Цель: развитие представление о математике как о живой области знаний;
– формирование методов действий в нестандартных ситуациях, умение находить более рациональные решения, не опирающиеся на алгоритмы и модели;
– формирование устойчивой мотивации для творческой, а затем и учебной математической деятельности;
– формирование умения грамотно излагать свои мысли в устной и письменной форме, задавать вопросы, вести дискуссию;
– формирование представления о математике как творческом виде деятельности;
– формирование культуры мышления учащихся.
Применяемые методы обучения: создание проблемной ситуации, познавательное и диалогическое проблемное изложение, игры на сообразительность, беседы, практические работы.
Содержание курса (16 часов, 1 час в неделю).
«Что такое математика?» (4 ч)
Исторические развитие математики. Математик как профессия. Как появляются математические знания? Кто придумал математику? Все ли знают математики?
«Математическая деятельность» (4 ч)
Как мы думаем? Что важнее интуиция или логика? Существует ли истина? Как связаны математика и Я? Как включиться в математику? Что такое «неизвестное и где оно прячется»?
«Математические задачи: так ли все сложно, как мне кажется» (4 ч)
Отличия задачи от ситуации. Математические задачи простые и сложные, стандартные и нестандартные. Что делать, когда не знаешь, как решить задачу?
«Инструменты в технологии поиска и решения задач» (4 ч)
Метод проб и ошибок. Метод мозгового штурма. Идеальный конечный результат.
Далее предлагается разработка креативного урока по теме: «Метод мозгового штурма» при нахождении площадей фигур [3].
Блок 1. Мотивация.
Учащиеся познакомились с понятием площади, были выведены формулы для нахождения параллелограмма, трапеции и треугольника.
Блок 2. Содержательная часть.
Первая серия заданий. Какие из следующих утверждений верны?
1. Площадь треугольника меньше произведения двух его сторон.
2. Площадь трапеции равна произведению основания трапеции на высоту.
3. Площадь квадрата равна произведению двух его смежных сторон.
4. Площадь параллелограмма равна половине произведения его диагоналей
5. Площадь прямоугольника равна произведению длин всех его сторон.
6. Любые два равновеликих параллелограмма равносоставлены.
Вторая серия заданий.
1. Как изменится площадь квадрата, если его сторону увеличить в 2 раза? в 3 раза? в 2^ раза? Как изменится площадь треугольника, если каждую его сторону увеличить в 2 раза? в 3 раза? в 2^ раза?
2. Как изменится площадь прямоугольника, если: а) одну пару противоположных сторон увеличить в два раза. б) каждую сторону увеличить в два раза. в) одну пару противоположных сторон увеличить в два раза, а другую - уменьшить в два раза?
3. Как провести две прямые через вершину квадрата, чтобы разделить его на три фигуры, площади которых равны?
Блок 3. Психологическая разгрузка.
В качестве психологической разгрузки могут быть использованы: дыхательная гимнастика; физические упражнения на гармонизацию развития полушарий головного мозга; психорегулирующие упражнения и аутогенная тренировка, обеспечивающие релаксацию, эмоциональную разгрузку и др.
Блок 4. Головоломки.
Третья серия заданий.
Найдите площади фигур (рис. 1):
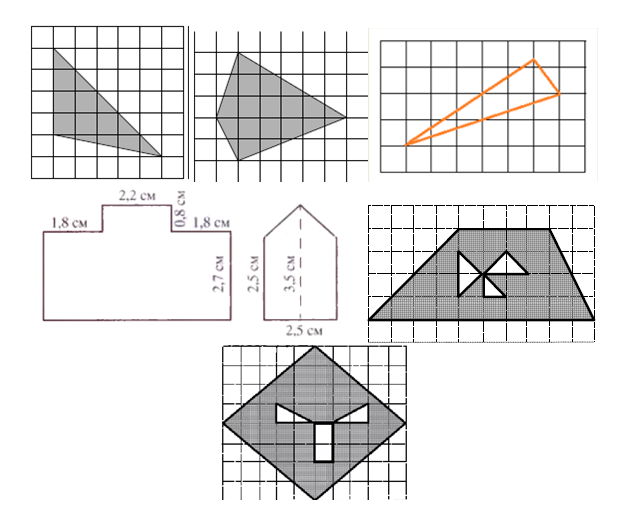
Рис. 1.
Блок 5. Содержательная часть.
Четвертая серия заданий.
1. Футбольное поле имеет форму прямоугольника, длина которого в 1,5 раза больше ширины. Площадь футбольного поля равна 7350 м2. Найдите его ширину.
2. Площадь участка земли равна 1200 м2. Чему равна его площадь на плане, если масштаб равен 1:100?
3. Найти площадь поверхности детали, изображенной на рисунке (рис. 2).
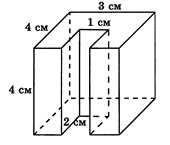
Рис. 2.
Блок 6. Интеллектуальная разминка с компьютерной интеллектуальной поддержкой мышления.
Пятая серия заданий. Предложите способ, с помощью которого можно измерить площадь земли, занимаемого торговым центром (или прудами, или парком) (например, рис. 3).
Предложите способ, с помощью которого можно измерить площадь поверхности торгового центра (например, рис. 4).

Рис. 3.

Рис. 4.
Заключение. Включение детей, неуспевающих по математике в дополнительные занятия, не связанные с «рутинной математической деятельностью», предусматривают возможность применения стандартных знаний в нестандартной ситуации, при выполнении таких заданий ученик может проявить способность к логическому и абстрактному мышлению, то есть умение классифицировать, обобщать и проводить аналогии, прогнозировать результат, применяя интуицию, воображение, фантазию, и, главное, способствовать развитию креативности.
Ссылки на источники
1. Гирш Т.С. Преодоление психологической инерции мышления у учащихся // НМЭЖ «Концепт». Т 2. 2013. С. 14-16.
2. Горев П.М., Утёмов В. В. Научное творчество: практическое руководство по развитию креативного мышления: Учебно-методическое пособие. – Книжный дом "ЛИБРОКОМ", 2014. – 112 с.
3. Кислякова М.А. Организация работы школьников над исследовательскими задачами на нахождение площади треугольника / М.А. Кислякова, К.Р. Сурова. // Материалы студенческой национальной научной конференции «Far East Math», г. Хабаровск, 2020. –212 с. – С. 171 – 176.
4. Клепников В.Н. Триз-математика в школе / В.Н. Клепников // Школьные технологии. 2018. № 2. С. 45-52.
5. Локалова Н.П. Школьная неуспеваемость: причины, психокорреция, психопрофилактика. – СПб.: Питер, 2009. 368 с
6. Утёмов В. В. Технология формирования креативного мышления на основе задач открытого типа // Вестник Сургутского государственного педагогического университета. - 2011. - № 3. - С. 51-57
7. Утёмов В. В., Горев П. М. Оценивание метапредметных результатов освоения программ общего образования на основе коэффициента интеллектуальности // Научно-методический электронный журнал «Концепт». – 2014. – № 4 (апрель). – С. 1–5. – URL: http://e-koncept.ru/2014/14079.htm.
8. Утёмов В. В., Зиновкина М. М. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ // Научно-методический электронный журнал «Концепт». – 2013. – Т. 3. – С. 2841–2845. – URL: http://e-koncept.ru/2013/53572.htm.
