Внеклассные мероприятия по математике по теме «Математический марафон» для учащихся 3

атематические игры, соревнования, турниры вызывают неподдельный интерес детей младшего и среднего возраста, как к возможности встретиться очно с ребятами из других школ, проявить свою эрудицию, знания.

Охват большого количества детей способствует «популяризации» математики, а также выявлению способных, талантливых учеников. Поддержка, создание условий для дальнейшего их развития является одной из основных задач современной школы.

Турнир «Математический марафон» на базе МБОУ «Гимназия № 26» для учащихся 3–4 классов г. Набережные Челны и близлежащих городов стал традиционным мероприятием. Задачи для турнира готовятся учителями гимназии таким образом, чтобы решения нельзя было бы найти в интернет-ресурсах. Проводится турнир накануне весенних каникул. Заявки для участия подаются по адресу, указанному на сайте гимназии. С результатами мероприятия участники могут ознакомиться также на сайте гимназии.

Цели:

1) способствовать прочному усвоению учебного материала; повышению уровня математического развития;

2) развивать творческое мышление, быстроту реакции, коммуникативные навыки;

3) воспитывать самостоятельность, волю; прививать интерес к предмету.

Этапы мероприятия.

«Математический марафон» состоит из нескольких этапов.

Первый этап: организационный. Прибытие и регистрация участников.

Второй этап: личная олимпиада. Участники получают задания и решают их в течение двух часов (примерный набор задач и критерии оценки в приложениях 1 и 2).

Третий этап: организационный. Обед. Подготовка команд к игре.

Четвертый этап: математическая командная игра на примере «Математического казино» (приложение 3).

Пятый этап: организационный. Подведение итогов личной олимпиады и математической игры. Награждение.

Олимпиада. 3 класс

1. Ширина прямоугольника 11 метров, а длина больше ширины на 13 дм. Найдите периметр прямоугольника.

2. Мотоцикл проехал расстояние 246 км между двумя пунктами за 3 часа. За какое время проедет это расстояние велогонщик, скорость которого в 4 раза меньше?

3. Петя доходит от дома до школы за 20 минут, а Вася добегает до школы и обратно без остановки за 10 минут. Во сколько раз скорость Васи больше, чем скорость Пети?

4. Веревку длиной 40 метров разрезали на два куска, один из которых вчетверо длиннее другого. Какова длина большего куска?

5. Если Вася даст Пете 125 рублей, то денег у них станет поровну. На сколько у Васи денег больше, чем у Пети?

6. Из трех квадратов, каждый периметра 16 дм, составили прямоугольник. Найдите периметр и площадь прямоугольника.

7. Сколько натуральных чисел между числами 123 и 321.

8. Петя решил 15 задач. Из них все, кроме шести, логические. Все логические, кроме трёх, на разрезание. Задачи на разрезание, кроме одной, решены неправильно. Сколько задач на разрезание Петя решил верно?

9. Найдите недостающее число: 4, 7, 13, 25, __, 97.

10. В одном пакете 5 кг конфет, а в другом – 12 кг тех же конфет. Второй пакет стоит на 1400 рублей дороже. Сколько стоит каждый пакет?

11. После олимпиады выяснилось, что Петя и Вася вместе решили 22 задачи, Вася и Толя вместе решили 25 задач, а Петя и Толя вместе решили 27 задач. Сколько задач решил каждый?

12. В клетках квадрата 3 × 3 записаны числа так, что суммы чисел в каждой строке, в каждом столбце и на каждой диагонали были одинаковыми. Некоторые числа стёрли. Восстановите стёртые числа.

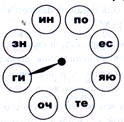
13. Мальчики стоят в очереди за сосисками в тесте. Петя – пятый, если считать с начала, Вася – восьмой, если считать с конца. Между ними стоит Толя. Сколько всего человек может стоять в очереди?

14. Папе столько лет, сколько месяцев его дочери. Вместе им 39 лет. Сколько лет каждому?

15. Петя и Вася стоят на дороге. Сейчас между ними 20 км. Какое расстояние будет между ними через два часа, если Петя пойдёт со скоростью 4 км/час, а Вася – 5 км/ч?

16. Разрежьте прямоугольник 6 × 9 на 8 квадратов.

17. Бутылочка «Кока-колы» весит 570 г. После того, как Петя выпил половину, она стала весить 345 г. Сколько весит бутылка «Кока-колы».

18. Придумайте семь различных чисел, которые отличаются только последней цифрой, а их сумма равна 2331. В ответ запишите их через запятую.

19. Четыре мороженых и пять пирожных весят 1 кг 400 г, а пять мороженых и четыре пирожных весят 1 кг 300 г. Сколько весит пирожное?

20. Возраст известного джина старика Хоттабыча записывается числом с различными цифрами. Об этом числе известно следующее: 1) если первую и последнюю цифру зачеркнуть, то получится двузначное число, которое при сумме цифр 14, является наибольшим; 2) первая цифра меньше последней в 4 раза. Сколько лет старику Хоттабычу?

Таблица 1

Задача	Ответ	Максимальный балл
1	46 м 6 дм	5б
2	через 12 часов	5б
3	в 4 раза	5б
4	32 м	5б
5	на 250 руб.	5б
6	32 дм и 48 дм²	5б - 2 верных ответа, 2б - 1 верный ответ, 0б - если хотя бы 1 неверный ответ
7	197	5б
8	Ответ дан в условии задачи: " Задачи на разрезание, кроме одной, решены неправильно". Верно решена одна задача.	5б
9	49	5б
10	1000 руб. и 2400 руб.	5б
11	Петя – 12 задач, Вася - 10,Толя –15 задач	5б
12		5б
13	10 или 14 человек	5б - 2 верных ответа, 2б - 1 верный ответ, 0б - если хотя бы 1 неверный ответ
14	36 лет и 3 года	5б
15	2, 38, 22 или 18 км	5б - 4 верных ответа, 3б - 3 верных ответа, 2б - 2 верных ответа, 1б - 1 верных ответа, 0б - если хотя бы 1 неверный ответ
16	проверить чертёж	5б
17	120 г	5б
18	330, 331, 332, 333, 334, 335, 336	5б
19	200 г	5б
20	1954 лет или 2958 лет	5б - 2 верных ответа, 2б - 1 верный ответа, 0б - если хотя бы 1 неверный ответ
ИТОГО баллов		100

Олимпиада. 4 класс

1.Четыре бегемота весят столько же, сколько 8 толстопузых тараканов. Один слон весит столько же, сколько 2 бегемота. Сколько толстопузых тараканов уравновесят одного слона?

2.Друзья составили задачу про Азата: наш друг Азат ест невкусную макаронину длиной 84 км. В первый день он съел седьмую часть всей макаронины, во второй – шестую часть оставшейся макаронины, а в третий день – пятую часть остатка. Сколько километров невкусной макаронины съедено Азатом за три дня?

3.Азат и Ильдар стоят на дороге. Сейчас между ними 30 км. Какое расстояние будет между ними через два часа, если Азат пойдёт со скоростью 4 км/час, а Ильдар побежит со скоростью – 8 км/ч?

4.Деревянный кубик весит 6 г. Сколько весит деревянный кубик с ребром вдвое большим?

5.В бочке было 56 ведер воды. Когда из нее отлили несколько ведер, то воды осталось в 7 раз больше, чем отлили. Сколько ведер отлили?

6.В одной капле воды сидит 2019 микробов, в другой капле микробов сидит в два раза больше, чем в первой, а в третьей – в 3 раза больше, чем во второй. Сколько микробов засядут в ученом с мировым именем Карл, если он перепутает эти капли с валерьянкой и выпьет их залпом?

7.Из чисел 427, 32, 7, 8, 94 и 4 составьте наименьшее десятизначное число, записывая их одно за другим в каком-то порядке.

8.Число х таково, что прибавить к нему 2 – то же самое, что умножить его на 3. Тогда умножить его на 6 – то же самое, что прибавить к нему…?

9.Дан числовой ребус: 9* ∙ ** = *9*

Какие цифры можно поставить вместо звездочек, чтобы получилось верное равенство? Первая звездочка в числе не может быть нулем. Записать все возможные равенства.

10.Какой это день недели, если он идет не вслед за понедельником и не перед четвергом, а завтра не воскресенье, а послезавтра будет не суббота и позавчера была не среда?

11.Азат весит 24 кг и еще треть собственного веса. Сколько весит Азат?

12.Предприниматель Ёлкин огородил кованой изгородью квадратный участок размером 98 м×98 м, поставив через каждые 2 м, начиная с угла, столбы. Сколько всего столбов в изгороди?

13.В ряд выписали 13 натуральных чисел так, что сумма любых трех соседних равна 24. На первом месте стоит 8, а на девятом – 7. Какое число стоит на втором месте?

14.В классе учится меньше, чем 50 школьников. За контрольную работу седьмая часть учеников получила пятерки, третья – четверки, половина – тройки. Остальные работы были оценены как неудовлетворительные. Сколько было таких работ?

15.У дамы спросили, сколько ей лет. Она ответила: «Тридцать два без суббот, воскресений и понедельников…». Сколько лет даме?

16.Сумма восьми последовательных чисел равна 2020. Найдите наименьшее из них.

17.Карлсон пошел в гости к Винни-Пуху, а в качестве гостинцев принес три банки меда. У Винни до этого было 6 банок меда. Сев за стол, Карлсон говорит: «Я могу съесть весь принесенный мною мед за 9 минут», а на что Винни ответил: «А я могу съесть 1 банку меда за 6 минут». Сколько времени потребуется «сладкоежкам» съесть весь мед, если они будут трапезничать одновременно?

18.Четвероклассник Ильдар заметил, что в примере на деление делитель в 4 раза меньше частного, а делимое в 5 раз больше частного. Ильдар сообщил эти данные Ленизе. Лениза восстановила пример. Восстановите и вы этот пример.

19.В некотором году в мае 4 понедельника и 4 пятницы. Какой день недели 1 мая?

20.В олимпиаде участвовали 5 человек. На каждый вопрос один из них дал неправильный ответ, остальные – правильный. Число правильных ответов у Азата равно 10 – меньше, чем у любого другого. Число правильных ответов у Ильдара равно 13 – больше, чем у любого другого. Сколько правильных ответов дал каждый из остальных участников?

Таблица 2

Задача	Ответ	Балл
1	4 таракана	5б
2	36 км	5б
3	6, 54, 38 или 22 км	5б - 4 верных ответа, 3б - 3 верных ответа, 2б - 2 верных ответа, 1б - 1 верных ответ, 0б - если хотя бы 1 неверный ответ
4	48 г	5б
5	7 вёдер	5б
6	18171 микробов	5б
7	3242747894	5б
8	5	5б
9	99 ∙ 10 = 990 или 90 ∙ 11 = 990	5б - 2 верных ответа, 2б - 1 верный ответ, 0б - если хотя бы 1 неверный ответ
10	ПОНЕДЕЛЬНИК или воскресенье	5б - 2 верных ответа, 2б - 1 верный ответ, 0б - если хотя бы 1 неверный ответ
11	36 кг	5б
12	196 столбов	5б
13	9	5б
14	1	5б
15	56 лет	5б
16	249	5б
17	за 18 минут	5б
18	100 : 5 = 20	5б
19	вторник	5б
20	по 11 правильных ответов	5б
ИТОГО баллов		100

Игра «Математическое казино»

Правила игры

В игре участвуют команды, состоящие из 4–6 человек. Игра состоит из шести блоков, на каждый из которых отводится по 15 минут. В каждом блоке командам выдаются карточки, содержащие 5 задач. В карточки игроками вносятся только ответы на каждую задачу, пишется название команды и ставка, какое количество задач команда, по мнению её игроков, решила правильно. Ставка может быть любым целым числом от 1 до 5. Задача считается решённой правильно, если указан правильный ответ. Если ответов в задаче несколько и приведены не все верные ответы, то ответ считается неправильным. Если среди верных ответов к задаче указан один или несколько неверных, то ответ также считается неправильным.

За каждую правильно решённую задачу команда получает 2 балла. За угаданное количество правильно решённых задач (правильную ставку) команда получает дополнительно бонус 5 баллов. Если команда решила правильно больше задач, чем указала в ставке, она получает баллы лишь за решённые задачи. Если команда решила правильно меньше задач, чем указано в ставке, то она получает баллы за решённые задачи и штраф за каждую недостающую задачу в 2 балла. Таким образом, в одном блоке можно набрать от – 10 до 15 баллов.

Побеждает команда, набравшая в результате 6 блоков наибольшее количество баллов.

Таблица 3

Математическое казино (3 класс)

		3 класс Блок 1 ЧИСЛА	Команда	Ставка
№	Задача			Ответ
1.	Найдите сумму цифр суммы цифр числа 20192019.
2.	Азат записал некоторое двузначное число, а Ильдар приписал к нему справа цифру 0. После этого изменения число увеличилось на 252. Какое число было записано Азатом?
3.	Сумма двух последовательных четных чисел равна 178. Найдите эти числа.
4.	Первая цифра пятизначного числа равна количеству нулей в этом числе. Вторая цифра – количеству единиц (цифр „1”) в этом числе. Третья цифра – количеству двоек, четвертая – количеству троек, пятая — количеству четвёрок. Придумайте такое число.
5.	Азат, путешествуя по Казани, зашел в трамвай и купил у кондуктора билет под номером 017262. Билет не оказался «счастливым», так как сумма первых трех цифр номера оказалась не равна сумме трех последних цифр. Кондуктор продает билеты по порядку номеров, т.е. номер следующего билета 017263. Сколько билетов нужно докупить Азату, чтобы ему достался ближайший «счастливый» билет?
		3 класс Блок 2 ВРЕМЯ, ВПЕРЁД!	Команда	Ставка
№	Задача			Ответ
1.	Фродо поинтересовался у бессмертного Леголаса: «Сколько тебе лет, эльф?». На что Леголас ответил: «Если к половине моих лет прибавить 1050 лет, то получишь мой возраст 401 год назад». Сколько сейчас лет Леголасу?
2.	Отец старше сына на 24 года. Сколько лет сыну, если через 2 года он будет в 7 раз моложе отца?
3.	Табло электронных часов показывает 15 : 12. Какое время будут показывать электронные часы в следующий раз, когда сумма часов и минут будет такой же?
4.	Табло электронных часов показывает 15 : 12. Какое время будут показывать электронные часы в следующий раз, когда сумма цифр на табло будет такой же?
5.	На доске записано число 51. Каждую минуту число стирают с доски и записывают на это место произведение его цифр, увеличенное на 13. Например, через минуту на доске запишут значение выражения 5·1+13, то есть 18. Какое число будет на доске через 100 минут?
		3 класс Блок 3 ГЕОМЕТРИЯ	Команда	Ставка
№	Задача			Ответ
1.	Три третьеклассника нарисовали круг, квадрат и треугольник. Азат: „Я нарисовал круг“. Ильдар: „Марсель нарисовал круг“. Марсель: „Я нарисовал квадрат“. Ровно один мальчик сказал неправду. Кто что нарисовал?
2.	У деревянного семиугольника отпилили один угол. Сколько углов осталось у получившейся фигуры?
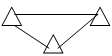
3.	Прямоугольник двумя прямолинейными разрезами разделите на четыре части так, что две из них – треугольники и две – четырёхугольники.
4.	Во дворе доктора Айболита построили бассейн для выздоравливающих пациентов. Зайчик выяснил, что его периметр — 20 метров, а белочка посчитала площадь — 24 квадратных метра. Каковы его длина и ширина?
5.	От некоторого прямоугольника отрезали квадрат, сторона которого равна меньшей стороне прямоугольника. От оставшейся части снова отрезали квадрат, сторона которого равна меньшей стороне полученного прямоугольника. После этого получился квадрат со стороной 3 см. Какие размеры мог иметь первоначальный прямоугольник?
		3 класс Блок 4 СЧАСТЛИВОЕ ДЕТСТВО	Команда	Ставка
№	Задача			Ответ
1.	Трое сладкоежек поделили между собой поровну 90 мармеладок. Первый съел несколько мармеладок, второй – столько, сколько не доел первый, а третий съел столько, сколько первые два вместе. Сколько мармеладок осталось у сладкоежек?
2.	В семье много детей. Семеро из них любят капусту, шестеро – морковь, пятеро – горох, четверо – капусту и морковь, трое – морковь и горох, двое – капусту и горох, а один – и капусту, и морковь, и горох. Сколько детей в этой семье, если таких, кто не любит ни капусту, ни морковь, ни горох, в этой семье нет?
3.	В третьем классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в биологическом, а 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?
4.	Азат увидел в буфете свою одноклассницу Аню. Народу было много, и Азат не видел, что покупала Аня, зато слышал ее слова: «Вот вам 3 монеты, здесь нужная сумма без сдачи. Спасибо!». Подойдя к прилавку, Азат увидел, что в буфете продается только это: леденец – 18 руб; яблоко – 22 руб; шоколадный батончик – 24 руб; мороженое – 33 руб; гамбургер – 40 руб. Найдите, что купила Аня? (Напомним, что у нас в стране есть только монеты 1, 2, 5, и 10 руб, а также копейки.)
5.	Аня попала в Зазеркалье, где встретила свое отражение – Яну. Потом Яна попала в свое Зазеркалье, где встретила свое отражение – конечно же, Аню-2! Аня-2 попала в свое Зазеркалье, где была Яна-2. И так происходило достаточно долго, пока зеркало не разбилось. Назовите, как звали 2019-ю девочку?
		3 класс Блок 5 АЗАТ и КВАДРАТ	Команда	Ставка
№	Задача			Ответ
1.	Азат выкладывает дно квадратной коробки квадратными конфетами. Он аккуратно уложил 28 конфет по краям коробки. Сколько всего ему понадобится конфет, чтобы покрыть дно коробки?
2.	Для окраски квадратного пола со стороной 5 м Азату требуется 5 кг краски. Сколько краски потребуется ему для окраски квадратного пола со стороной 10 м?
3.	Азат согнул аккуратно квадратный лист 4 раза и проколол шилом насквозь. Сколько дырок получилось на развернутом листе.
4.	Азат разрезал квадрат со стороной 1 м на квадраты со стороной 4 см и выложил в ряд. Найдите длину ряда.
5.	Из квадрата со стороной 15 см вырезали квадрат со стороной 12 см. Оставшийся кусок разрезали на единичные квадратики (это можно сделать), из которых Азат хочет сложить новый квадрат. Чему будет равна его сторона?
		3 класс Блок 6 РАБОТА не ВОЛК…	Команда	Ставка
№	Задача			Ответ
1.	Турист зажег первое полено, и разгорелся костер. Каждый час надо подбрасывать полено. Через сколько часов он положит в костер 15 полено?
2.	Железный Дровосек одним ударом топора разбивает любой чурбак или полено на три части. Он хочет разбить чурбак на 33 части. Сколько ударов ему понадобится?
3.	В тридцатилитровую бочку наливают каждый час 5 литров воды. На дне бочки есть дыра, через которую ежечасно выливается 3 литра воды. Через сколько часов бочка будет полной?
4.	Дюймовочка, убежав от крота, сначала ехала на гусенице 18 мин, а потом пересела на стрекозу и пролетела в 6 раз больший путь. Сколько минут она летела на стрекозе, если стрекоза летает в 12 раз быстрее, чем ползёт гусеница?
5.	Ильдар помогал маме готовить домашние пельмени. Он раскатал пласт теста и нарезал его на 20 одинаковых квадратов, но один из них упал и его пришлось выбросить. Потом из каждого квадрата Ильдар выдавливал стаканом круг из теста и отдавал его маме (для лепки одного пельменя). Тесто, оставшееся от каждых четырех квадратных заготовок, Ильдар снова раскатывал и получал один новый такой же квадрат. Какое наибольшее количество пельменей можно приготовить из 19 квадратных заготовок?

Таблица 4

3 класс. Казино (ответы)

Блок 1 ЧИСЛА

1. 6

2. 28

3. 88 и 90

4. 21200

5. 43

Блок 2 ВРЕМЯ, ВПЕРЁД

1. 2902

2. 2

3. 16 : 11

4. 15 : 21

5. 18

Блок 3 ГЕОМЕТРИЯ

1. Азат – круг, Ильдар – треугольник, Марсель - квадрат

2. 8

3. проверять чертёж!!!

4. 6 м и 4 м

5. 3 × 9 или 9 × 6

Блок 4 СЧАСТЛИВОЕ ДЕТСТВО

1. 30

2. 10

3. 6

4. ЯБЛОКО

5. Аня - 1010

Блок 5 АЗАТ и КВАДРАТ

1. 64

2. 20

3. 16

4. 25 м

5. 9 см

Блок 6 РАБОТА НЕ ВОЛК

1. 14

2. 16

3. 15

4. 9

5. 25

Таблица 5

Математическое казино (4 класс)

		4 класс Блок 1 СЧАСТЛИВОЕ ДЕТСТВО	Команда	Ставка
№	Задача			Ответ
1.	В семье много детей. Семеро из них любят капусту, шестеро – морковь, пятеро – горох, четверо – капусту и морковь, трое – морковь и горох, двое – капусту и горох, а один – и капусту, и морковь, и горох. Сколько детей в этой семье, если таких, кто не любит ни капусту, ни морковь, ни горох, в этой семье нет?
2.	В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в биологическом, а 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?
3.	Азат увидел в буфете свою одноклассницу Аню. Народу было много, и Азат не видел, что покупала Аня, зато слышал ее слова: «Вот вам 3 монеты, здесь нужная сумма без сдачи. Спасибо!». Подойдя к прилавку, Азат увидел, что в буфете продается только это: леденец – 18 руб; яблоко – 22 руб; шоколадный батончик – 24 руб; мороженое – 33 руб; гамбургер – 40 руб. Найдите, что купила Аня? (Напомним, что у нас в стране есть только монеты 1, 2, 5, и 10 руб, а также копейки.)
4.	Аня попала в Зазеркалье, где встретила свое отражение – Яну. Потом Яна попала в свое Зазеркалье, где встретила свое отражение – конечно же, Аню-2! Аня-2 попала в свое Зазеркалье, где была Яна-2. И так происходило достаточно долго, пока зеркало не разбилось. Назовите, как звали 2019-ю девочку?
5.	Юля и Аня делали уроки. Каждая из них начала с математики, затем выучила стихотворение, следом прочитала текст на английском языке и, наконец, выполнила упражнение по русскому языку. На каждый предмет у Юли уходило в два раза меньше времени, чем на предыдущий, а у Ани — в 4 раза меньше времени, чем на предыдущий. Начали и закончили они одновременно. Что делала Аня, когда Юля взялась за русский язык?
		4 класс Блок 2 ЧИСЛА	Команда	Ставка
№	Задача			Ответ
6.	Чему равна утроенная сумма половины и четверти числа 128?
7.	Найдите сумму цифр всех трехзначных чисел, которые можно составить из цифр 5, 7, 9 без повторений.
8.	К 4-хзначному числу прибавили сумму его цифр и получили 2019. Какие четырехзначные числа удовлетворяет этому условию?
9.	Для записи страниц при их нумерации потребовалось всего 2052 цифры. Найдите сколько всего страниц в этой книге.
10.	Найдите все семерки последовательных натуральных чисел, что сумма четырех первых равна сумме трех последних из них.
		4 класс Блок 3 ГЕОМЕТРИЯ	Команда	Ставка
№	Задача			Ответ
1.	Известно, что в одном футе 12 дюймов. Сколько квадратных дюймов в 7 квадратных футах?
2.	Каков объём прямоугольного параллелепипеда размером 2см на 2 мм и на 2 м? Ответ дать в кубических сантиметрах.
3.	Марсель перегнул прямоугольный лист бумаги по прямой так, что получился многоугольник, возможно невыпуклый. Какое количество сторон у него могло получиться?
4.	Имеется 99 маленьких кубиков с ребром в 1 см. Из них сооружается самый большой из возможных кубиков. Сколько маленьких кубиков осталось неиспользованными?
5.	На стороне АС треугольника АВС отметили точку Е. Известно, что периметр треугольника АВС равен 26 см, треугольника АВЕ – 15 см, треугольника ВСЕ – 17 см. Найдите длину отрезка ВЕ.
		4 класс Блок 4 ВРЕМЯ, ВПЕРЁД!	Команда	Ставка
№	Задача			Ответ
1.	Табло электронных часов показывает 15 : 12. Какое время будут показывать электронные часы в следующий раз, когда сумма часов и минут будет такой же?
2.	Когда моему отцу был 31 год, мне было 8 лет, а теперь отец старше меня вдвое. Сколько лет мне теперь?
3.	Венере было 15 лет 18 месяцев назад, а Марсу будет 18 лет через 15 месяцев. Кто из них старше и на сколько?
4.	На вопрос «Сколько тебе лет?» был получен ответ: «Если число, равное моему возрасту, умножить на сумму цифр этого числа, то получится 418» Чему равен возраст?
5.	На доске записано число 61. Каждую минуту число стирают с доски и записывают на это место произведение его цифр, увеличенное на 13. Например, через минуту на доске запишут значение выражения 6·1+13, то есть 19. Какое число будет на доске через 100 минут?
		4 класс Блок 5 ЕДЕМ – ЕДЕМ…	Команда	Ставка
№	Задача			Ответ
1.	В тридцатилитровую бочку наливают каждый час 5 литров воды. На дне бочки есть дыра, через которую ежечасно выливается 3 литра воды. Через сколько часов бочка будет полной?
2.	Дюймовочка, убежав от крота, сначала ехала на гусенице 18 мин, а потом пересела на стрекозу и пролетела в 6 раз больший путь. Сколько минут она летела на стрекозе, если стрекоза летает в 12 раз быстрее, чем ползёт гусеница?
3.	Азат проехал от дома бабушки до своего дома столько километров, сколько минут он ехал. С какой скоростью он ехал?
4.	Шестнадцати старшеклассникам было поручено вырыть отводную канаву от забора до обеда (дабы спасти школу от тающего снега). Когда школьники начали копать, в столовой для них начали готовить обед. Стараниями ребят канава за час становится длиннее на 3 метра; обед готовится со скоростью 4 порции в час. Какой длины получится канава, когда начнется обед?
5.	Вдоль береговой дорожки на равном расстоянии друг от друга стоят флажки. Старт дан у первого флажка. Через 6 минут бегун был у шестого флажка. У какого флажка он будет через 18 минут после старта? Скорость бегуна постоянная.
		4 класс Блок 6 ПОНЕМНОГУ ОБО ВСЁМ	Команда	Ставка
№	Задача			Ответ
1.	В «Гимназии № 26» 1076 учащихся. В рамках участия в экологической акции «Батарейки, сдавайтесь» некоторые из них принесли по одной батарейке, а половина оставшихся по две батарейки. Сколько всего батареек собрали учащиеся гимназии?
2.	В Линизиной квартире имеется 10 розеток, но ей их не хватает, чтобы включить все электроприборы. Поэтому она использует тройники – удлинители. Тройник устроен так, что он включается в розетку и из него получается 3 новые розетки. У Линизы всего 14 тройников. Какое наибольшее количество электрических приборов Линиза сможет включить в сеть одновременно?
3.	У меня 78 метровых поленьев, а у соседа — 78 двухметровых. Мои поленья распилили на полуметровые за полдня. Сколько потребуется времени на распиливание его поленьев на полуметровые?
4.	Из 15 шариков можно сложить равносторонний треугольник, но нельзя сложить квадрат – одного шарика не хватит. Из какого количества шариков не превосходящего 50, можно сложить и треугольник и квадрат?
5.	По договору с попом Балде причитается 30 полушек за каждый отработанный день, а за каждый неотработанный день с него взыскивается 6 полушек. Через 30 дней Балда узнал, что ему ничего не причитается и он ничего не должен. Сколько дней он работал?

Таблица 6

4 класс. Казино (ответы)

Блок 1 СЧАСТЛИВОЕ ДЕТСТВО

1. 10

2. 6

3. яблоко

4. Аня - 1010

5. учила стихотворение

Блок 2 ЧИСЛА

1. 288

2. 126

3. 2013 и 1995

4. 720

5. 9, 10, 11, 12, 13, 14, 15 –единственная семёрка чисел

Блок 3 ГЕОМЕТРИЯ

1. 1008

2. 80

3. 4, 5, 6, 7, 8, 9сторон

4. 35 кубиков

5. 3

Блок 4 ВРЕМЯ, ВПЕРЁД

1. 16 : 11

2. 23

3. Марс старше Венеры на 3 месяца

4. 38

5. 20

Блок 5 ЕДЕМ – ЕДЕМ…

1. 15

2. 9

3. 60 км/ч

4. 12 м

5. у 16 флажка

Блок 6 ПОНЕМНОГУ ОБО ВСЁМ

1. 1076

2. 38

3. один с половиной день (полтора дня)

4. 36

5. 5

Участие школьников в различных турнирах, играх, соревнованиях предполагает кропотливую, систематическую работу на уроках математики, на кружковых занятиях. Именно здесь дети приобретают необходимые знания, получают бесценный опыт решения задач, поиска оптимальных решений, выдвижения гипотез и их доказательств, отстаивания собственной точки зрения.

Ниже предлагается набор задач для одного из таких кружковых занятий.

Система задач по теме «Симметрия» для учащихся 6 классов

В программе математики 6 класса изучаются геометрические фигуры и их свойства. Для углубления материала используются кружковые занятия. Во время проведения последних в занимательной форме можно изучить достаточно серьезные свойства и признаки фигур без строгого обоснования. В данной части статьи рассмотрим примерный набор задач для проведения такого занятия по теме «Симметрия».

Симметрия одно из основных понятий математики. Свойством симметрии обладают не только геометрические фигуры, но и объекты природы. Важно и то, что симметрия имеет широкую область применения, например, в свойствах функций или в уравнениях. Также симметрия, являясь инвариантом, применяется как метод обоснования. Поэтому школьникам будет интересно продолжить знакомство с этим понятием, развивая свой кругозор и мышление.

Для проведения занятия необходимо приготовить раздаточный материал: бумажные модели фигур, листочки с задачами.

В начале занятия заслушивается небольшое сообщение о симметрии в природе и в жизни. Задание подготовить выступление по теме выдается учащимся заранее. Представляемая информация о симметрии должна содержать наглядный материал.

Затем учащимся предлагается набор задач. При решении последних школьниками понимается ценность метода симметрии, как способа доказательства или вычисления.

Задачи

1. Докажите, что в равностороннем треугольнике все углы равны. Определите величину каждого угла.

2. Докажите, что биссектриса, проведенная к основанию равнобедренного треугольника, является медианой и высотой.

3. Укажите точки, находящиеся на равном расстоянии от двух заданных А и В.

4. В треугольнике найдите точку, равноудаленную от его вершин.

5. Сформулируйте обратное утверждение к задаче 2, выясните, является ли оно истинным.

6. В треугольнике ХYZ ХY=5, YZ=6, ХZ=8. Прямая, проходящая через вершину Y перпендикулярно биссектрисе угла YХZ, пересекает ХZ в точке А. Через точку А проведена прямая, перпендикулярная биссектрисе угла ХZY, которая пересекает YZ в точке В. Через точку В проведена прямая, перпендикулярная биссектрисе угла ХYZ, пресекающая YХ в точке С. Найти длину ХС.

7. Докажите, что диаметр окружности, перпендикулярный к хорде, делит хорду и стягиваемые ею дуги пополам.

8. Шашку, находящуюся на клетке A, можно передвигать только на одну клетку вправо, вниз или вправо-вниз. Каких способов больше: попасть в клетку B или в клетку C? (рис.1)

Рис. 1.

9. Укажите центрально-симметричные фигуры.

10. Докажите, что любая прямая, проходящая через центр симметрии прямоугольника, делит его на равновеликие фигуры.

11. Маша и Миша по очереди кладут пятаки а) на круглый стол так, чтобы они полностью находились на столе и не перекрывали друг друга (стол достаточно велик для того, чтобы вместить хотя бы один пятак). Проигрывает тот, кто не сможет положить очередной пятак. Кто выигрывает при правильной игре? б) на квадратный стол; в) на прямоугольный стол, в центре которого вырезана круглая дырка, в которую проваливается пятак. [1]

Задачи для самостоятельного решения

1. В треугольнике АВС биссектриса АЕ равна отрезку ЕС. Найдите угол АВС, если АС = 2АВ.

2. Докажите, что против катета прямоугольного треугольника, который в два раза меньше гипотенузы, лежит угол в два раза меньший другого острого угла.

3. Найдите точку, равноудалённую от вершин четырёхугольника АВСD (рис.2).

Рис. 2.

4. В прямоугольнике прорезали дырку, также имеющую форму прямоугольника. Маша хочет разрезать полученную фигуру с дыркой на две фигуры равной площади. В ее распоряжении нет ничего, кроме карандаша и линейки без делений. Удастся ли ей это сделать?

5. Доска 8 ´ 8. За ход можно положить доминошку на любое свободное место. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре?

6. Придумайте свою задачу, при решении которой используется симметрия.

Ответы. Указания
1. Дети подтверждают это высказывание на бумажных моделях, используя прием наложения. Этот же метод применяется при доказательстве теорем на уроках геометрии 7 класса.

Для определения величины угла равностороннего треугольника необходимо до проведения занятия кружка вывести гипотезу о сумме углов треугольника.

2. При доказательстве свойства равнобедренного треугольника на бумажных моделях используется осевая симметрия.

3. Детям выдается листок неровной формы с отмеченными на нем двумя точками. Середину отрезка АВ дети находят быстро. Чтобы найти остальные точки, нужно согнуть листок так, чтобы точки совместились.

4. Использовать задачу №3. Если к моменту проведения кружка на уроках математики были изучены простейшие построения с помощью циркуля и линейки, то найти точку можно не только на бумажной модели.

5. Формулируется и обосновывается признак равнобедренного треугольника.

6. Ответ: 2. При решении используется задача № 5.

8. Ответ: одинаково. Использовать осевую симметрию относительно диагонали квадрата, проходящей через клетку А.

11. Можно спросить и про параллелограмм. И вообще, стол может иметь форму любой центрально-симметричной фигуры.

Решение задач можно осуществить на нескольких занятиях. Необходимо учитывать разнообразие форм и содержания кружка в силу возрастных особенностей младших школьников. Важно поддерживать интерес к систематическим занятиям. С формами проведения кружка можно ознакомиться в учебном пособии «Уроки развивающей математики. 5–6 классы: Задачи математического кружка» авторов Горев П. М. и Утёмов В. В. [2].

Ссылки на источники

Генкин С. А., Итенберг И. В., Фомин Д. В. Ленинградские математические кружки. – Киров: Изд-во «АСА», 1994. – 272 с.
Горев П. М., Утёмов В. В. Уроки развивающей математики. 5–6 классы: Задачи математического кружка: Учебное пособие. – Киров: Изд-во МЦИТО, 2014. – 207 с.

Скачать публикацию

Внеклассные мероприятия по математике по теме «Математический марафон» для учащихся 3–4 классов

Похожие публикации

Внеклассные мероприятия по математике по теме «Математический марафон» для учащихся 3–4 классов

Свидетельство

Похожие публикации