Быстро меняющийся современный рынок труда предъявляет к выпускнику школы требования, которые нашли свое отражение в федеральных государственных образовательных стандартах общего образования и в примерных основных образовательных программах. Конкурентоспособным сегодня является работник, который не только хорошо знает особенности своей профессии, но и имеет четкий математический стиль мышления, проявляющийся во владении обширным арсеналом интеллектуальных умений и навыков.
Математика, как учебный предмет, имеет большие возможности для развития не только предметных, но и универсальных учебных действий и практических навыков моделирования реальных объектов, и поэтому является ключевой учебной дисциплиной для многих профилей обучения. В результате изучения математики «обучающиеся развивают логическое и математическое мышление, получают представление о математических моделях; овладевают математическими рассуждениями; учатся применять математические знания при решении различных задач и оценивать полученные результаты» [1, стр. 11].
Геометрия, важнейший компонент математического образования, знания по которому будут востребованы в любой сфере профессиональной деятельности, позволяет сформировать у школьника представление о фигурах и измерениях. «Хорошее пространственное воображение, развиваемое геометрией, – отмечает Н.Ф. Четверухин, [2, с. 7], – нужно конструктору, создающему новые машины, геологу, разведывающему недра земли, архитектору, сооружающему здания современных городов, хирургу, производящему тончайшие операции среди кровеносных сосудов и нервных волокон, скульптору, художнику и т.д.»
Геометрия позволяет формировать наряду с пространственным воображением широкий спектр личностных и метапредметных результатов за счет использования методов, идущих от наглядных представлений и эффективных при решении не только геометрических, но и многих задач других наук. «Геометрия занимает особое место в науке, – утверждает А.Д. Александров [3, c. 72], – т.к. с нею связано идущее от пространственных представлений точное синтетическое мышление, часто позволяющее охватить в целом то, что достигается анализом и выкладками лишь через длинную цепь шагов. Геометрия характеризуется не только своим предметом, но и методом, идущим от наглядных представлений и оказывающимся плодотворным в решении многих задач других наук»
В тоже время освоение геометрического материала зачастую вызывает затруднения у обучающихся. Еще Эвклид отмечал, что «нет царского пути в геометрии», т.е. нет простого и легкого способа изучения геометрии, так как решение каждой геометрической задачи – это небольшое открытие, которое не может быть алгоритмизировано. Затруднение вызывает построение чертежа к задаче, анализ условия, оформление решения. Поэтому многие школьники при выполнении работ государственной итоговой аттестации приступают к решению задач из раздела «Геометрия» в последнюю очередь. Таким образом, можно констатировать недостаточно высокий уровень усвоения геометрических знаний выпускниками общеобразовательных организаций.
Об этом свидетельствуют и результаты государственной итоговой аттестации. При общей тенденции к увеличению процента выпускников, успешно сдавших экзамен по математике по программам основного общего образования, наблюдается снижение процента решивших геометрические задачи. Так, в 2018 г. снизился по сравнению с 2017 процент учащихся, решивших задачи по темам «Треугольник», «Окружность» и «Площадь многоугольника», задание на распознавание ошибочных заключений; по отдельным геометрическим задачам базового уровня процент выполнения не достиг 30%.
На основе анализа типичных ошибок школьников, не справившихся с заданиями раздела «Геометрия», можно сделать вывод:
- о недостаточности геометрических знаний (некоторые выпускники не владеют знаниями по геометрии в необходимом объеме, затрудняются в использовании справочного материала);
- о несформированности базовой логической культуры (обучающиеся не умеют делать выводы, путают причины и следствия, делают ошибочные умозаключения);
- недостаточном уровне графической культуры (большинство ошибок при решении геометрических задач связано с неправильным построением чертежа или неверном чтении данных с уже готового чертежа к задаче, например, вместо
ÐАВС = 440, читают Ð АСВ = 440).
ÐАВС = 440, читают Ð АСВ = 440).
Таким образом, существуют пробелы в знаниях выпускников, обусловленные многими причинами, в том числе, недостаточным вниманием преподавателей к вопросам обучения геометрии.
Однако, при анализе образовательных запросов учителей математики, в рамках курсов повышения квалификации не выявлено запросов в методической поддержке процесса обучения геометрии. При самообследовании компетенций в рамках развития субъектной позиции учителя в педагогическом сообществе [4, с.10] учителя математики всего 14,7% педагогов отметило дефицит по данному вопросу, что свидетельствует о недостаточной внимании специалистов к рассматриваемой проблеме.
Для изучения уровня сформированности предметных компетенций педагогов с целью их дальнейшей корректировки во время курсов повышения квалификации учителям математики был предложен ряд задач, в том числе, по геометрии.
Структура блока геометрических задач представлена в таблице 1
Таблица 1
Задания блока «Геометрия»
|
Номер задания |
Тема |
Код элементов содержания, проверяемые заданиями КИМ |
Максимальное количество баллов |
Уровень |
Обязательное задание |
|
Геометрия |
|||||
|
1 |
Планиметрия. Вписанные и описанные многоугольники |
8.1 |
1 |
Базовый |
Обязательное |
|
2 |
Стереометрия. Площадь поверхности и объем многогранников |
8.4 – 8.7 |
1 |
Базовый |
Обязательное |
|
3 |
Стереометрия |
8.2-8.12 |
2 |
Повышенный |
По выбору |
|
4 |
Планиметрия |
8.1 |
3 |
Повышенный |
По выбору |
Задачи 1 и 2 были обязательными для выполнения. При среднем уровне выполнения заданий базовой части работы в 82,8%, можно считать полученные результаты в 70% и 74% недостаточно высокими, результат невозможно объяснить только вычислительными ошибками.
Во время выполнения работы учителя математики могли выбирать четыре задания повышенного уровня из семи предложенных, среди которых были две геометрические задачи (3 и 4 в таблице 1 на рисунке 1). Предполагалось, что задания, с которыми учителя хорошо знакомы и не вызывают затруднений, будут выбираться чаще. Задачи по геометрии выбирались крайне редко, процент решаемости данных задач (6% и 2%) совпадает с процентов педагогов, выбравших их.
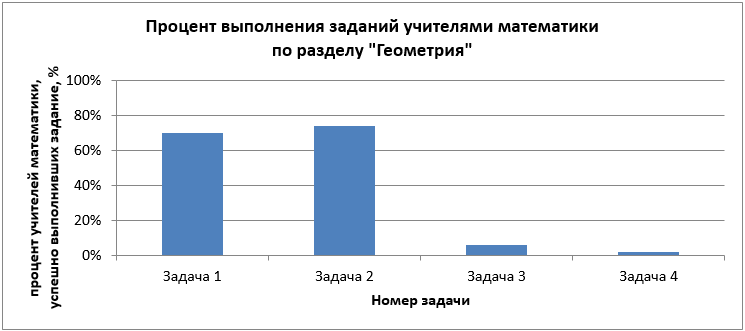
Рисунок 1 – Результаты выполнения заданий по разделу «Геометрия»
в ходе исследования предметных компетенций учителей математики
Из проведенного исследования можно сделать вывод, что учителя математики затрудняются при решении задач по геометрии как базового, так и повышенного уровня.
В соответствии с полученными результатами на курсах повышения квалификации был сделан акцент на решение геометрических задач и методику обучения геометрии в курсе школы.
Учителя математики отмечают, что успешному усвоению материала мешает, прежде всего, низкая учебная мотивация школьников, а также чрезмерная внимательность начинающего педагога к научности изложения материала в ущерб развитию навыков решения практических задач.
Для освоения геометрического материала школьниками учителю необходимо правильно выбрать наиболее эффективные методы обучения.
К традиционным методам обучения относят объяснительно – иллюстративный метод Главная задача учителя при применении данного метода сводится к изложению материала, например в процессе мини-лекции с поддержкой наглядных средств. Основное достоинство данного метода – он экономичен по времени, можно предложить школьнику большой объем информации. С успехом используется при систематизации знаний, обобщении материала на этапе подготовке к ГИА в старших классах. Недостаток метода – слабая активность школьников в процессе обучения, что не позволяет сформировать устойчивых знаний по геометрии у обучающихся с низким уровнем обученности.
Репродуктивный метод – организация учебной деятельности по определенной инструкции с применением (или воспроизведением) полученных ранее знаний и последовательности практических действий. При репродуктивном построении рассказа учитель в готовом виде формулирует определения, выводы, предлагает алгоритм решения задач. Метод дает хороший результат при использовании на уроках алгебры, использование его на уроках геометрии зачастую затруднено спецификой геометрических задач.
С целью достижения результативности обучения применяются инновационные методы обучения: активные и интерактивные, которые нацелены на «умение выделять главное, делать сравнение, устанавливать причинно-следственные связи и делать умозаключения, а также видеть смысл в информации, понимать проблему в целом» [5].
Активные предусматривают деятельную позицию учащегося по отношению к преподавателю и к тем, кто получает образование вместе с ним. Благодаря интерактивным методам, происходит эффективное усвоение знаний в сотрудничестве с другими учащимися. Эти методы принадлежат к коллективным формам обучения, во время которых над изучаемым материалом работает группа учащихся, при этом каждый из них несет ответственность за проделанную работу.
Рассмотрим применение инновационных методов обучения на уроках геометрии на примере урока - бенефиса одной задачи.
Класс разбивается на группы. Каждая группа получает условие задачи и теоретический справочный материал, который подводит группу к выбору определенного способа решения задачи. Свое решение каждая группа представляет классу, в ходе обсуждения анализируется эффективность данного способа.
Приведем пример задачи, которую можно решить несколькими способами.
«На гипотенузе прямоугольного треугольника, как на стороне, построен квадрат в той полуплоскости от прямой, содержащей гипотенузу, которой не принадлежит треугольник. Найти расстояние от вершины прямого угла до центра квадрата, если его катеты имеют длины а и b». Её можно решить, используя теорему синусов; теорему косинусов; теорему Птолемея; метод площадей; метод геометрических преобразований; метод координат; описав около исходного квадрата квадрат со стороной (а + b) и другие.
В рамках курсов повышения квалификации учителей математики рассматривается возможность использования традиционных и инновационных методов обучения и их эффективность, особенности геометрического материала..
Например, в 5-6 классах необходимо:
1. широко использовать фузионистский подход к обучению основам геометрии. Данный подход предполагает параллельное обучение планиметрии и стереометрии, когда плоские и пространственные фигуры изучаются совместно, дополняя и развивая каждую составляющую часть геометрии Обучающимся необходимо предлагать задания, направленные на поиск связи между плоскими и пространственными фигурами, а так же с предметами окружающей действительности;
1. широко использовать фузионистский подход к обучению основам геометрии. Данный подход предполагает параллельное обучение планиметрии и стереометрии, когда плоские и пространственные фигуры изучаются совместно, дополняя и развивая каждую составляющую часть геометрии Обучающимся необходимо предлагать задания, направленные на поиск связи между плоскими и пространственными фигурами, а так же с предметами окружающей действительности;
2. важно из урока в урок демонстрировать связь геометрии с жизнью. Геометрические факты должны иллюстрироваться примерами из архитектуры, изобразительного искусства, промышленного дизайна, природы. Это позволит опираться на жизненный опыт обучающегося при объяснении нового материала, подчеркнет практическую значимость геометрии, что повысит мотивацию к ее изучению;
3. в процессе изучения тем геометрии ученики должны научиться классифицировать геометрические фигуры, находить общее и различие между геометрическими объектами, строить логические умозаключения при решении задач на вычисление и построение. Особое внимание необходимо уделить формированию изобразительно-графических умений. Приоритетными для этого возраста являются инновационные методы обучения;
4. развитие интереса к геометрии поддерживают занимательные задачи: логические игры, лабиринты, оригами, математический паркет и другие позволяют поддерживать интерес к изучению геометрии на достаточно высоком уровне.
При обучении геометрии в 7-9 классах важно подчеркнуть практическую значимость курса и тот факт, что геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимым для многих специалистов.
Например, при изучении темы углы можно обсудить, какие инструменты используются на практике для измерения углов, чем они отличаются, в какой профессии используются. При изучении темы «Многоугольники» – понятие жесткой фигуры, использование ее свойств при моделировании предметов быта. Можно рассмотреть применение треугольников для придания устойчивости различным конструкциям – столбам линии электропередач, телевизионным вышкам, попросить школьников найти другие примеры окружающей действительности. С другой стороны, параллелограмм не является жесткой фигурой и это позволяет использовать его при моделировании жалюзи, раздвижных ворот, подъемных механизмов и т.п.
Важнейшим направлением работы учителя математики является педагогическое стимулирование познавательного интереса. Понятие «стимулирование» связано с опосредованным воздействием на внутреннюю мотивацию человека посредством побуждения его к мысли, чувству и действию. К стимулам, основанным на содержании учебного материала, относятся его практическая значимость для самого ребёнка и степень сложности.[6, с. 64 ]
Существенную роль в формировании геометрических знаний играют задания с практическим содержанием, позволяющие продемонстрировать обучающихся как, используя геометрические знания можно решить повседневные задачи. Задачи с практическим содержанием можно использовать на учебных занятиях в формате деловой игры, круглого стола, проектно-исследовательской работы, кейс-метода.
Для качественного усвоения геометрических знаний необходимо максимально приблизить содержание задачного материала к жизненному опыту обучающихся. Использование задач с региональной тематикой подчеркнет значимость математического знания, поможет обучающемуся освоить приемы решения жизненных задач с использованием геометрических сведений, «будет способствовать популяризации инженерных и технических профессий, подвигнет обучающихся на исследования различных аспектов развития агропромышленного комплекса на территории региона, познакомит с инновационными продуктами, производимыми на территории Челябинской области» [7].
Приведем пример задачи, составленной с опорой на региональный материал.
Задача. Труба ЧЭМК была построена более полувека назад и входила в пятерку самых высоких промышленных сооружений города Челябинска. В 2014 г. труба была демонтирована.
При высоте солнца в 56˚ заводская труба бросала тень длиной 81 м. Используя таблицу тригонометрических функций, найдите высоту трубы. В ответе укажите приближенное значение, выражаемое целым числом метров.
При разработке задач с опорой на региональные особенности необходимо, по мнению Уткиной Т.В.[8, с. 27], ориентироваться на следующие предметные результаты:
– овладение основными навыками получения, применения и интерпретации информации математического содержания об объектах региона, города, поселения, использования математических знаний в повседневной жизни;
– формирование представлений о математике, её роли в жизни и профессиональной деятельности человека, необходимость применения математических знаний для решения современных практических задач региона;
– формирование представлений об особенностях деятельности людей, ведущей к развитию промышленности родного края, формирование представлений о реальном промышленном секторе Челябинской области.
Одним из ключевых методов обучения является проектно-исследовательский метод, который позволяет выявить творческие способности учащихся, приводит к высоким предметным, метапредметным и личностным результатам. Метод проектов ставит учителя в позицию сотрудничества с учащимися, но иногда учителя математики затрудняются в выборе тем проектных и исследовательских работ и организации индивидуальной и группой работы обучающихся.
В рамках курсов повышения квалификации данные вопросы освещаются максимально полно, педагоги не только осваивают теоретический материал, но и в ходе деловой игры, мастер-классов и круглых столов определяют возможности применения и условия эффективности предложенных методов и приемов обучения. Рассмотренные в статье подходы к преподаванию позволят повысить качество обучения школьников геометрии.
Ссылки на источники
- Приказ Минобрнауки России от 17.12.2010 N 1897 «Об утверждении Федерального государственного образовательного стандарта основного общего образования Сетевой ресурс. URL: https://fgos.ru/LMS/wm/wm_fgos.php?id=osnov, стр. 11
- Четверухин Н.Ф. Изображение фигур в курсе геометрии./ Н.Ф. Четвертухин. - М.: Педагогика, 1958 - 216 с.
- Александров А.Д. Избранные труды— Новосибирск: Наука, 2008. — Т. 3 (Статьи разных лет). – 734 с.
- Хаджиева М.В. Модель развития субъектной позиции учителя в педагогическом сообществе в общеобразовательной организации / М.В. Хаджиева //
Научное обеспечение системы повышения квалификации кадров. 2018. № 2 (35). С.9-14. - Пяткова О.Б. Формирование стратегий смыслового чтения текстовой информации у обучающихся // О.Б. Пяткова Научно-методический электронный журнал «Концепт». – 2017. – No V7 – URL: http://e-kon-cept.ru/2017/170162.htm.5
- Коликова Е.Г. Система развития технических способностей учащихся на основе использования эвристических методов и ТРИЗ в проектной деятельности / Е.Г. Коликова // Современные проблемы науки и образования.- 2018.- № 4.– С. 60-65.
- Бегашева И.С. Специфика отражения национальных, региональных и этнокультурных особенностей региона при разработке рабочих программ по физике / И.С. Бегашева // Современные научные исследования в сфере педагогики и психологии [Электронный ресурс]: сборник результатов научных исследований / Электрон. текст. дан. – Киров: Изд-во МЦИТО, 2018
- Уткина Т.В. Формирование целостностного содержания естественно-научного образования при профильном обучении / Т.В. Уткина // Биология в школе. 2012. № 7. С. 24-30
