Задачи:
- повышение уровня математического мышления,
- углубление теоретических знаний,
- расширение кругозора,
- возникновение интереса к математике,
- воспитание стремления к совершенствованию своих знаний,
- способ организации свободного досуга учащихся,
- формирование умений коллективного поиска ответов на вопросы,
- сплочение коллектива,
- формирование дружеских, товарищеских отношений,
- выявление творческих и организаторских способностей детей.
Цели:
- Формировать познавательную активность и широту кругозора.
- Учить учащихся совместной деятельности, формировать дисциплинированность, ответственность за дело коллектива.
- Учить рациональному использованию досуга.
Оборудование:
- Высказывания о математике.
- Фото математиков.
Ребята, вы много раз читали и слышали такие высказывания в адрес математики:
- Математика – это язык, на котором говорят все точные науки (Н. И. Лобачевский).
- Математику уже затем учить надо, что она ум в порядок приводит (М. В. Ломоносов).
- Вдохновение нужно в геометрии не меньше, чем в поэзии. (А. С. Пушкин).
Всё это верно!
Математика – строгая, любящая точность наука, но математика может быть интересной, познавательной и весёлой. Сейчас мы будем заниматься математическими вопросами, но в дружеской соревновательной форме. Соревнование будет проходить между двумя командами.
1-й этап – «Кто мы?» создание и название команд
Название команд определяется после I конкурса: назвать имена математиков, которые прозвучали при изучении тем по математике 6 класса в I полугодии.
(На классной доске, предварительно скрытые, расположены рисунки с изображением математиков, упомянутых в учебнике 6 класса). Отгадывая ученых, команды зарабатывают соответствующие очки.
В зависимости от набранных очков, команды по очереди выбирают имя ученого – название команды.
Пифагор – изучал вопрос о делимости чисел (5).
Эратосфен – придумал способ отыскания простых чисел (6).
Евклид – доказал, что простых чисел бесконечно много (7).
Эйлер – нашел 65 дружественных чисел (8).
Виноградов – доказал, что любое нечетное число, большее 5, можно представить в виде суммы трёх простых чисел (9).
2-й этап – выбор капитана.
Кто первый вычислит предложенный пример в каждой из команд – считается капитаном. Первоочередность хода следующего этапа определяется очередностью вычисления примера. ответ: .
3-й этап – разминка
Каждой команде за минуту ответить на вопросы.
За каждый ответ балл. Чем больше отвеченных вопросов – больше баллов.
Вопросы для 1-й команды:
1. Числа, употребляемые при счете (натуральные).
2. Число, не являющееся ни составным, ни простым (единица).
3. Дробь, у которой числитель больше знаменателя. (неправильная).
4. Инструмент для построения окружности в тетради (циркуль).
5. Из двух чисел на координатной прямой то число больше, которое расположено… (правее).
6. Скорость, умноженная на время (расстояние).
7. Результат деления (частное).
8. Натуральное число, имеющее более двух делителей (составное).
9. Выражение, находящееся над дробной чертой (числитель).
10. Сотая часть числа (процент).
11. Инструмент для измерения и построения отрезков в тетради (линейка).
12. Равенство двух отношений (пропорция).
13. Результат сложения (сумма).
14. Расстояние, деленное на время (скорость).
Вопросы для 2-й команды:
1. При сложении (вычитании) обыкновенных дробей дроби приводят к… (общему знаменателю).
2. Две дроби, произведение которых равно единице (взаимно обратными).
3. Вычисление дроби от числа находят... (умножением).
4. Длина прямоугольника, умноженная на ширину (площадь).
5. Результат решения уравнения (корень).
6. Из двух чисел на координатной прямой то число меньше, которое расположено … (левее).
7. Результат вычитания. (разность).
8. Инструмент для вычисления прямых углов (угольник).
9. Натуральное число, имеющее только два делителя: единицу и само себя. (простое).
10. Выражение, находящееся под дробной чертой (знаменатель).
11. Число, содержащее в записи запятую (десятичная дробь).
12. Инструмент для измерения и построения углов в тетради (транспортир).
13. Результат деления (частное).
14. Расстояние, деленное на скорость. (время).
4-й этап – «Мы знаем»
(На классной доске, предварительно скрытые, расположены листы с новыми математическими понятиями, изучаемые в курсе 6 класса в I полугодии).
Нужно назвать все новые понятия с их определением, изучаемые в курсе 6 класса I полугодия. Начинает та команда, которая первая решила пример на предыдущем этапе. Если окажутся не открыто всё табло предоставляется право ответа другой команде и т. д.:
- пропорция (5),
- отношение (6),
- НОД (7),
- НОК (7),
- простые числа (9),
- составные числа (10),
- взаимно простые числа (11),
- взаимно обратные числа (12).
5-й этап - физкультминутка «Не скажу» или «Один за всех»
Ученики по порядку называют числа. Вместо чисел, которые делятся на 3, говорят: «Не скажу». Тот, кто ошибается, выбывает из игры. Оставшийся победитель приносит команде столько очков сколько человек в команде.
6-й этап – Волшебная лавка
В импровизированной лавке предлагается выбрать и решить задачи разного уровня сложности. Ребята, решив задачи, смогут получить 1баллов, 3 балла, 5 баллов. Уровень сложности выбирают сами. Решают либо по одному, либо группами, либо все вместе.
Задачи на 1 балл
Задача № 1.
Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то как не знать.
Но совсем другое дело –
Быстро, точно и умело
Треугольники считать.
Например, в фигуре этой
Сколько разных? Рассмотри!
Всё внимательно исследуй
И по краю, и внутри!
Сколько треугольников изображено на рисунке? (рис. 1, 2)
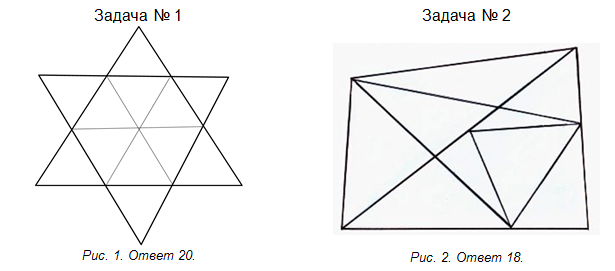
Задача № 3. В записи 1*2*3*4*5 замените «*» знаками действий и расставьте скобки так, чтобы получилось выражение, значение которого равно 100.
Ответ: 1 ∙ (2 + 3) ∙ 4 ∙ 5 = 100.
Задача № 4 Найдите сумму: 1 + 2 + 3 + … + 111.
Ответ: 6 216
Задачи на 3 балла
Задача № 1. Пришел Иван-царевич в подземелье к Кощею Бессмертному Василису Прекрасную освобождать. В подземелье три темницы. В одной из них томится Василиса, в другой расположился Змей Горыныч, а третья темница – пустая. На дверях есть надписи, но они все ложные. На первой темнице написано: «Здесь Василиса Прекрасная»; на второй темнице: «Темница №3 не пустая»; на третьей темнице написано: «Здесь Змей Горыныч». В какой же темнице Василиса?
Ответ: Василиса Прекрасная не может быть в первой темнице, значит она во второй или третьей. Так как темница 3 – пустая, то Василиса Прекрасная будет во второй темнице.
Задача № 2. На столе стоят 3 ящика, в одном находится 2 черных шарика, в другом – 1 черный и 1 белый шарик, а в третьем – 2 белых шарика. На ящиках написано «2 белых», «2 черных», «черный и белый». При этом известно, что ни одна из надписей не соответствует действительности. Как, вынув только 1 шарик. Определить правильное расположение надписей?
Ответ: Можно вынуть шарик из ящика «черный и белый». а) если окажется шар белый, значит в данном ящике 2 белых шара, в ящике «2 черных» лежат белый и черный, а в 3-м лежат черные шары. Случай б) если окажется шар черный, рассуждаем аналогично (Табл. 1)
Таблица 1
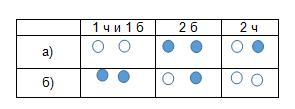
Задача № 3. Как разрезать торт тремя прямыми так. Чтобы получилось семь частей и на каждой из них была розочка? (рис. 3, 4)

Задачи на 5 баллов
Задача № 1. Ехали два крестьянина и нашли три бочонка: один восьмиведёрный с квасом и два пустых – пятиведёрный и трёхведёрный. Крестьяне решили поделить квас поровну тут же на месте с помощью этих трёх бочонков. Как они это сделали?

Ответ: табл. 2
Таблица 2
|
8 ведёрн
|
5 ведёрн
|
3 ведёрн
|
|
8
|
0
|
0
|
|
5
|
0
|
3
|
|
5
|
3
|
0
|
|
2
|
3
|
3
|
|
2
|
5
|
1
|
|
7
|
0
|
1
|
|
7
|
1
|
0
|
|
4
|
1
|
3
|
|
4
|
4
|
0
|
Задача № 2. Как набрать из реки ровно 6 литров воды, если имеются два ведра: одно 1 емкостью 4 л, другое – 9 л?
Ответ: табл. 3
Таблица 3
|
4 л
|
9 л
|
|
0
|
9
|
|
4
|
5
|
|
0
|
5
|
|
4
|
1
|
|
0
|
1
|
|
1
|
9
|
|
4
|
6
|
Задача № 3. Разделите двумя прямыми на шесть частей фигуру, изображенную рисунке 6.
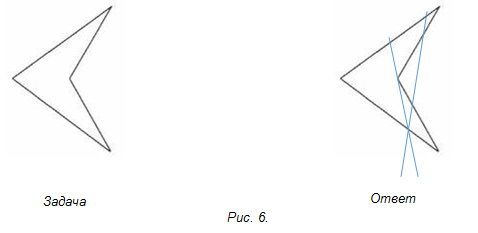
Подводятся итоги игры-соревнования. Слово жюри.
Результаты каждого конкурса жюри фиксируют в таблице (табл. 4), и подводит итоги.
Для жюри:
Таблица 4
|
Команда
|
Кто мы?
|
разминка
|
Мы знаем
|
Заморочки из мешочка
|
Физкульт минутка
|
Волшебная лавка
|
Итог
|
|
I ком
|
|
|
|
|
|
|
|
|
II ком
|
|
|
|
|
|
|
|
Использование наряду с разнообразными традиционными уроками, итоговые внеклассные мероприятия такого плана, на мой взгляд, реализует ряд задач как математического интереса, мышления и кругозора, так и коммуникативные. Так же дети приобщаются к культуре и истории математики.
Ссылки на источники:
1. Математика. 5 кл.: учеб. для общеобразоват. учреждений / Г.К. Муравин, О. В. Муравина. – 2-е изд., стереотип. –М. : Дрофа, 2013.
2. Математика. 5 кл.: учеб. для общеобразоват. организаций с прил. на электрон. носителе/С. М. Никольский, М.К. Потапов, Н. Н. Решетников, А.В. Шевкин. – 13-е изд., Просвешение, 2014.





