Необходимость развития личности с широким интеллектуальным потенциалом отражена в Федеральных и региональных документах, в том числе, в Федеральном государственном образовательном стандарте основного общего образования [1].
В статье описан пример использования педагогической системы НФТМ-ТРИЗ М. М. Зиновкиной в изучении теоремы Пифагора в 8 классе [2].
1. Блок мотивации. Математика как теория получила развитие в школе Пифагора (571–479 гг. до н.э.). Главной заслугой пифагорейцев в области науки является существенное развитие математики как по содержанию, так и по форме. По содержанию – открытие новых математических фактов. По форме – построение геометрии как теоретической, доказательной науки, изучающей свойства отвлечённых понятий о геометрических формах. Дедуктивное построение геометрии явилось мощным стимулом её дальнейшего роста. Вершиной достижений пифагорейцев в планиметрии является доказательство теоремы Пифагора. Последняя за много столетий раньше была сформулирована вавилонскими, китайскими и индийскими учёными, однако её доказательство им не было известно.
В статье описан пример использования педагогической системы НФТМ-ТРИЗ М. М. Зиновкиной в изучении теоремы Пифагора в 8 классе [2].
1. Блок мотивации. Математика как теория получила развитие в школе Пифагора (571–479 гг. до н.э.). Главной заслугой пифагорейцев в области науки является существенное развитие математики как по содержанию, так и по форме. По содержанию – открытие новых математических фактов. По форме – построение геометрии как теоретической, доказательной науки, изучающей свойства отвлечённых понятий о геометрических формах. Дедуктивное построение геометрии явилось мощным стимулом её дальнейшего роста. Вершиной достижений пифагорейцев в планиметрии является доказательство теоремы Пифагора. Последняя за много столетий раньше была сформулирована вавилонскими, китайскими и индийскими учёными, однако её доказательство им не было известно.
Имя Пифагора обросло огромным количеством легенд. По преданию, Пифагор родился на острове Самос, что находится в Эгейском море недалеко от побережья Малой Азии. Свою школу он основал в г.Кротоне на юге Италии. Организованный им союз был не только школой, но и братством аристократов. Членам братства запрещалось разглашать открытия своей школы. Скрытность пифагорейцев не дают возможность понять, какие математические результаты принадлежат именно Пифагору. Считается, что он открыл доказательство теоремы, носящей теперь его имя. В ознаменование этого события философ, как рассказывают, принёс в жертву быка (по иным версиям – сто быков). И важно то, что свойство прямоугольного треугольника было установлено не случайно, не опытом, не измерением, а исключительно путём доказательства, т.е. только усилием человеческого разума. Вот именно с этого момента, когда убедились, что путём логических рассуждений можно открывать новые факты, и пошла геометрия как дедуктивная наука [3].
2. Блок творческого разогрева. Ещё две с половиной тысячи лет назад египтяне знали, что в треугольнике со сторонами 3,4, 5 локтей один угол прямой, но объяснить этого не могли. Вы заметили, что 3,4, 5 – не случайные числа. Смотрите: 3х3=9, 4х4=16, 5х5=25. А если теперь сложить два первых результата, то получится третий. (Попробуйте отыскать ещё несколько троек чисел, обладающих тем же свойством). Оказывается, стороны такого треугольника обладают каким-то особым свойством. Это видно из рисунка 1. Две с половиной тысячи лет назад Пифагор доказал, что в любом прямоугольном треугольнике стороны обладают тем же свойством.
2. Блок творческого разогрева. Ещё две с половиной тысячи лет назад египтяне знали, что в треугольнике со сторонами 3,4, 5 локтей один угол прямой, но объяснить этого не могли. Вы заметили, что 3,4, 5 – не случайные числа. Смотрите: 3х3=9, 4х4=16, 5х5=25. А если теперь сложить два первых результата, то получится третий. (Попробуйте отыскать ещё несколько троек чисел, обладающих тем же свойством). Оказывается, стороны такого треугольника обладают каким-то особым свойством. Это видно из рисунка 1. Две с половиной тысячи лет назад Пифагор доказал, что в любом прямоугольном треугольнике стороны обладают тем же свойством.
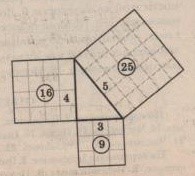
Рис.1. Египетский треугольник
Существует около 500 доказательств теоремы Пифагора. Мы познакомимся с некоторыми из них.
3. Теоретический блок. Вот несколько формулировок теоремы Пифагора, переведённых с латинского и греческого языка. «В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол». «Площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу». Современная формулировка: «Квадрат гипотенузы равен сумме квадратов катетов» (рис.2).
3. Теоретический блок. Вот несколько формулировок теоремы Пифагора, переведённых с латинского и греческого языка. «В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол». «Площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу». Современная формулировка: «Квадрат гипотенузы равен сумме квадратов катетов» (рис.2).
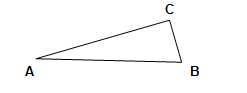
Рис. 2. Прямоугольный треугольник
Дано: ∆АВС, ÐС=90°.
Доказать: АС2+ВС2=АВ2
Попробуем найти несколько способов доказательств этого утверждения.
1. Проведём СD^АВ.
1. Проведём СD^АВ.
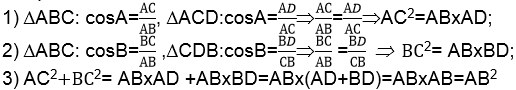
2. Обозначим стороны треугольника АВ=с, ВС=а, АС=b. Достроим треугольник до квадрата со стороной а+ b. (рис.3). Докажите, что синим цветом выделен тоже квадрат.
Sкв=(а+ b)2=4Sтр +Sкв¢=4х1/2а b+с2=2а b+ с2
а2+2а b+ b2=2а b+ с2
а2+ b2= с2
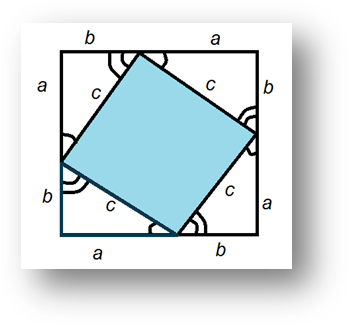
Рис. 3. Доказательство теоремы Пифагора, используя площади
4. Блок примеров.
4. Блок примеров.
Задания.
- Найти длину лестницы, приставленной к дому, если один её конец находится на расстоянии 4 м от другого, а другой – на стыке стены и крыши. Высота дома равна 8 м.
- Бамбуковый ствол в 9 футов высотой переломлен бурей так, что если верхнюю часть его пригнуть к земле, то верхушка коснётся земли на расстоянии 3 футов от основания ствола. На какой высоте переломлен ствол? [3]
- 5. Блок экспериментов [4].
Эксперимент 1. Доказательство может быть произведено на фигуре, в шутку называемой «Пифагоровы штаны» (рис.4). Идея его состоит в преобразовании квадратов, построенных на катетах, в равновеликие треугольники, составляющие вместе квадрат гипотенузы.
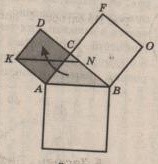Рис.4. Пифагоровы штаны∆АВС сдвигаем, как показано стрелкой, и он занимает положение ∆КDN. Оставшаяся часть фигуры АКDСВ равновелика площади квадрата АКDС – это параллелограмм АКNВ.
Сделана модель параллелограмма АКNВ голубого цвета. Параллелограмм перекладываем так, как зарисовано. Чтобы показать преобразования параллелограмма в равновеликий треугольник, на глазах учащихся отрезаем на модели треугольник и перекладываем его вниз.
Таким образом, площадь квадрата АКDС получилась равна площади прямоугольника. Аналогично преобразуем площадь квадрата в площадь прямоугольника.
Произведём преобразования для квадрата, построенного на катете а.
а) квадрат преобразуется в равновеликий параллелограмм.
б) параллелограмм поворачивается на четверть оборота.
в) параллелограмм преобразуется в равновеликий прямоугольник (рис.5).
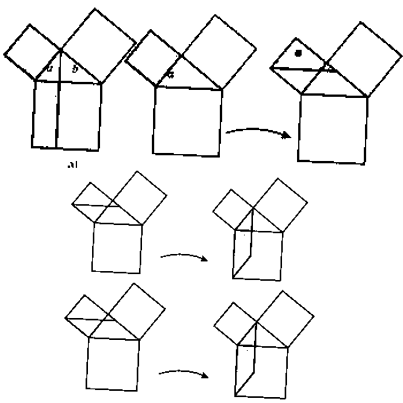
Рис.5. Доказательство теоремы Пифагора
Эксперимент 2. Доказательство, изобретённое арабским математиком Сабитом ибн Коррой. Сначала чертим рядом два квадрата, построенных на катетах, а затем, отрезая и переставляя получившиеся фигуры, складываем из них квадрат гипотенузы. (рис.6).
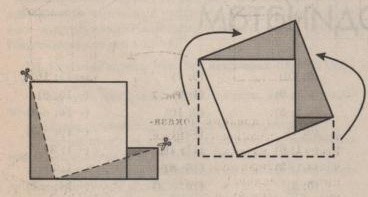Рис. 6. Доказательство Сабита ибн Корра
6. Теоретический блок 2. Ещё два доказательства теоремы Пифагора, основанные на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.
Рис. 6. Доказательство Сабита ибн Корра6. Теоретический блок 2. Ещё два доказательства теоремы Пифагора, основанные на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.
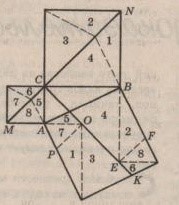
Рис.7. Доказательство Энштейна
Здесь (рис.7): АВС – прямоугольный треугольник с прямым углом С; СÎМN;СК^МN;РО‖МN;ЕF‖МN/
Рис.8. Разбиение ан-Найризия
Здесь (рис.8) доказательство теоремы Пифагора сделано с помощью разбиения средневекового багдадского комментатора «Начал» Евклида ан-Найризия. В этом разбиении квадрат, построенный на гипотенузе, разбит на 3 треугольника и 2 четырёхугольника. Здесь: АВС – прямоугольный треугольник с прямым углом С; DЕ=ВF.
7. Блок примеров 2. Перед вами (рис.9) две разновидности пифагоровых деревьев – фигур, получающихся при бесконечном повторении во всё меньшем масштабе знаменитых «пифагоровых штанов». Каждое из пифагоровых деревьев обладает замечательным свойством самоподобия: любой фрагмент дерева при надлежащем увеличении (и повороте) совпадает совсем деревом. Такие геометрические объекты получили название фракталов и сейчас широко используются в науке и искусстве.
Здесь (рис.8) доказательство теоремы Пифагора сделано с помощью разбиения средневекового багдадского комментатора «Начал» Евклида ан-Найризия. В этом разбиении квадрат, построенный на гипотенузе, разбит на 3 треугольника и 2 четырёхугольника. Здесь: АВС – прямоугольный треугольник с прямым углом С; DЕ=ВF.
7. Блок примеров 2. Перед вами (рис.9) две разновидности пифагоровых деревьев – фигур, получающихся при бесконечном повторении во всё меньшем масштабе знаменитых «пифагоровых штанов». Каждое из пифагоровых деревьев обладает замечательным свойством самоподобия: любой фрагмент дерева при надлежащем увеличении (и повороте) совпадает совсем деревом. Такие геометрические объекты получили название фракталов и сейчас широко используются в науке и искусстве.
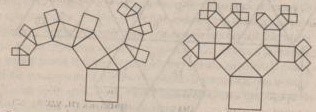
Рис.9. Фракталы.
8. Блок экспериментов 2. Решение задач с применением теоремы Пифагора.
8. Блок экспериментов 2. Решение задач с применением теоремы Пифагора.
Эксперимент 3. Дан отрезок, длина которого равна единице измерения. Построить отрезок, Длина которого равна и таких отрезков.
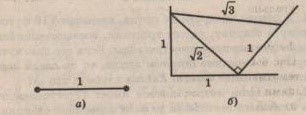
Рис.10. Построение отрезка, равного и единичного отрезка
Эксперимент 4. Параллельно прямой дороге на расстоянии 500 м от неё расположена цепь стрелков. Расстояние между крайними стрелками равно 120 м, дальность полёта пули равна 2,8 км. Какой участок дороги находится под обстрелом этой цепи?
Решение (рис.11).
АН2=2,82-0,52, АН»2,755 (км), АВ= 2х2,755+0,12»5,63 (км)
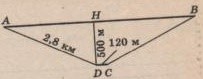
Рис.11. Чертёж к задаче.
В блоке экспериментов на уроках математики, можно использовать задачи открытого типа. Задачи открытого типа имеют размытое условие, из которого недостаточно ясно как действовать, что использовать при решении, но понятен требуемый результат. Разнообразие путей решения, которые не является «прямолинейными», двигаясь по которым попутно приходиться преодолевать возникающие «препятствия». Вариантов результата решения много, нет понятия «правильное решение»: решение либо применимо к достижению требуемого условия, либо нет. Поэтому, можно говорить об эффективности, оптимальности и оригинальности выбранного решения [5].
9. Блок резюме. О теореме Пифагора. Стихотворение Шамиссо.
9. Блок резюме. О теореме Пифагора. Стихотворение Шамиссо.
Суть истины вся в том, что нам она – навечно.
Когда хоть раз в прозрении её увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна.
Список табу, составленный Пифагором для членов своего ордена.
1) Делай лишь то, что впоследствии не омрачит тебя и не заставит раскаяться;
2) Не делай никогда того, чего не знаешь, но научись всему, что нужно знать;
3) Либо молчи, либо говори то, что ценнее молчания.
На следующих уроках мы продолжим изучать теорему Пифагора и её применение.
Ссылки на источники
- Федеральный государственный образовательный стандарт основного общего образования. Федер. закон РФ от 17 декабря 2010 г. № 1897-ФЗ.
- Зиновкина М.М. НФТМ-ТРИЗ : Креативное образование ХХI века. Теория и практика.-М.:МГИУ, 2008.-306 с.
- Глейзер Г.И. История математики в школе. VII-VIII (8-9) классы/Пособие для учителей. – М., Просвещение, 1982.
- Барыбин К.С., Добрынин И.Н. Сборник задач по геометрии для 7-8 классов рабочей молодёжи. – М., Учпедгиз, 1961.
- Утёмов В. В. Задачи открытого типа как средство развития креативности учащихся средней школы // Концепт: научно-методический электронный журнал официального сайта эвристических олимпиад «Совёнок» и «Прорыв». – 4 квартал 2011, ART 11-4-02. – Киров, 2011 г. – URL: http://www.covenok.ru/koncept/2011/11402.htm. – Гос. рег. Эл № ФС 77-46214. – ISSN 2225-1618
Zhuravleva Tatyana Alekseevna,
the teacher of mathematics of MKOU Krasnooktyabrskoi OOSH village Chuvashi Kirovo-Chepetsk District Kirov Region
krasnoshka@mail.ru
Lesson «Pythagorean Theorem»
Abstract. The article deals with the double lesson of studying Pythagorean Theorem with the help of pedagogical system NFTM-TRIZ by M. M. Zinovkina.
Key words: Pythagorean Theorem, NFTM-TRIZ, a lesson of mathematics