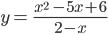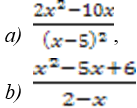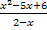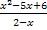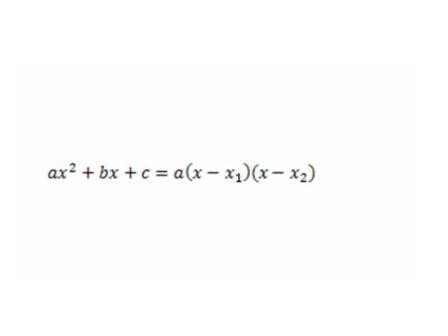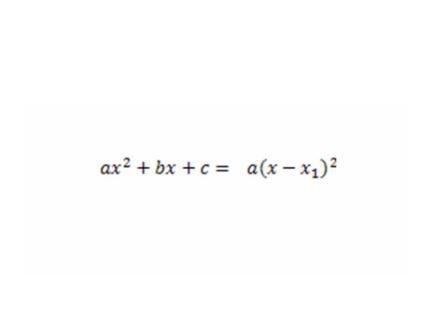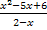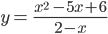Цель урока: создать содержательные и организационные условия для восприятия, осмысления и первичного закрепления учащимися правила разложения квадратного трёхчлена на множители.
Задачи:
- обучающие: научить учащихся раскладывать на множители квадратный трёхчлен, научить применять алгоритм разложения на множители квадратного трехчлена при решении примеров, рассмотреть задания базы данных ГИА, в которых используется алгоритм разложения квадратного трёхчлена на множители
- развивающие: развивать у школьников умение формулировать проблемы, предлагать пути их решения, содействовать развитию у школьников умений выделять главное в познавательном объекте.
- воспитательные: помочь учащимся осознать ценность совместной деятельности, содействовать развитию у детей умений осуществлять самоконтроль, самооценку и самокоррекцию учебной деятельности.
Формы работы учащихся: фронтальная работа, работа в парах, индивидуальные задания, групповая работа.
Оборудование:мультимедийный проектор, экран, компьютер, дидактический материал, учебники, тетради, презентация к уроку
Структура и ход урока
|
№ |
Этап урока |
Деятельность учителя (с указанием действий с ЭОР) |
Деятельность ученика |
Время (в мин.) |
|
Организационный момент. Мотивация учащихся.
Сообщение этапов урока, организация обучающихся на выполнение работы. |
1.Организационный момент: учитель приветствует учащихся, проверяет готовность к уроку. Мотивирует учащихся: - Сегодня на уроке в совместной деятельности мы подтвердим слова Пойа (Слайд 1).(«Задача, которую вы решаете, может быть очень скромной, но если она бросает вызов вашей любознательности, и если вы решаете ее собственными силами, то вы сможете испытать ведущее к открытию напряжение ума и насладиться радостью победы». (Двердь Пойа.) Сообщение о Пойа (Слайд 2) -Я хочу сделать вызов вашей любознательности. Рассмотрим задание из ГИА. Постройте график функции. - Как решить эту проблему? - Наметить план действий для решения этой проблемы.
Корректирует план урока, комментирует принцип самостоятельной работы. |
Составление плана урока
|
|
|
Актуализация субъективного опыта.
Стадия вызова
Формулирование темы урока, постановка цели урока.
|
Самостоятельная работа (классу раздать листочки с текстом самостоятельной работы) (Приложение 1) Самостоятельная работа 1) Разложите на множители: a) x 2 – 3x; b) x 2 – 9; c) x 2 – 8x+16; d) 2a 2 – 2b 2 –a+b; e) 2x 2 – 7x– 4. 2) Сократить дробь:
Слайд С ответами для самопроверки. Вопрос классу: - Какие способы разложения многочлена на множители вы использовали? - Все ли многочлены вы смогли разложить на множители? -Все ли дроби смогли сократить? Проблема2: Слайд - Как разложить на множители многочлен 2x 2 – 7x – 4? -Как сократить дробь Фронтальный опрос: - Что собой представляют многочлены 2x 2 – 7x – 4 и x 2 – 5x +6? -Дайте определение квадратного трёхчлена. - Что мы знаем о квадратном трёхчлене?
- Как найти его корни?
- От чего зависит количество корней?
- Сопоставьте эти знания с тем, что мы должны узнать и сформулируйте тему урока. ( После этого на экране тема урока) Слайд
- Поставим цель урока Слайд
- Наметим конечный результат Слайд
|
Решение самостоятельной работы в тетрадях
Самопроверка по слайду
- Вынесение множителя за скобку, способ группировки, использование формул сокращенного умножения. - Нет. 2x2 – 7x – 4. - Нет.
-Данные многочлены являются квадратными трёхчленами. -Квадратным трехчленом называется многочлен вида ах2 +bx+c , где х -переменная, a, b, c- некоторые числа, причем а¹ 0. -Чтобы найти корни квадратного трехчлена ах2 +bx-+c , надо решить квадратное уравнение вида ах2 +bx-+c =0 -От значения дискриминанта квадратного уравнения, если D > 0 - два корня, если D = 0 – один корень, если D<0 – корней нет.
Тема урока «Разложение квадратного трёхчлена на множители».
Научиться раскладывать квадратный трехчлен на множители и применять данные знания при выполнении упражнений
Уметь раскладывать квадратный трехчлен на множители и применять данные знания при выполнении задания из ГИА и других упражнений |
|
|
Изучение нового учебного материала. Стадия осмысления
Стадия рефлексии
|
Вопрос классу: Как решить эту проблему? Класс работает в группах. Задание группам: по оглавлению найти нужную страницу, с карандашом в руках прочитать п.4 , выделить главную мысль, составить алгоритм, по которому любой квадратный трёхчлен можно разложить на множители. Проверка выполнения задания классом (фронтальная работа): -Какова главная мысль пункта 4? Слайд (на экране формула разложения квадратного трёхчлена на множители ). Алгоритм на экране. Слайд 1.Приравнять квадратный трёхчлен к нулю. 2.Найти дискриминант. 3.Найти корни квадратного трёхчлена. 4.Подставить найденные корни в формулу. 5.Если необходимо, то внести старший коэффициент в скобки. -Ещё одна маленькая проблема: если D=0, то можно ли разложить квадратный трёхчлен на множители, и если можно, то как? (Исследовательская работа в группах). Слайд (на экране: Если D = 0, то Если квадратный трехчлен не имеет корней, то его разложить на множители нельзя.)
-Вернёмся к заданию в самостоятельной работе. Сможем ли теперь разложить на множители квадратные трёхчлены 2x 2 – 7x – 4 и x 2 – 5x +6? Класс работает самостоятельно, раскладывает на множители, я работаю индивидуально со слабыми учащимися. Слайд (с решением) Взаимопроверка |
Работа учеников с текстом учебника, карандашом делают пометки на полях. Учащиеся работают в группах.
Сверяют полученный алгоритм с алгоритмом на экране.
Учащиеся выводят формулу
Да.
Самостоятельная работа
Взаимопроверка |
|
|
Закрепление изученного материала |
Сможем ли сократить дробь Сократить дробь, вызываю к доске сильного ученика. Вернёмся к заданию из ГИА. Сможем ли мы теперь построить график функции Что является графиком данной функции? Постройте график функции у себя в тетради. Тест (самостоятельная работа) Приложение 2 Самопроверка и самооценка Учащимся выданы листочки (Приложение 3), в которые надо записать ответы. В них даны критерии оценок. Критерии оценок: Верно выполнено: 2 задание – оценка«3» 3 задания – оценка»4» 4задания – оценка «5» |
Ученик у доски сокращает дробь, а остальные работают в тетрадях
Прямая Выполняют задание в тетради. Индивидуальное выполнение теста.
Самопроверка по слайду |
|
|
Итог урока |
Рефлексия: (слайд) 1. Сегодня на уроке я научился… 2. Сегодня на уроке я повторил… 3. Я закрепил… 4. Мне понравилось… 5. Я поставил себе оценку за деятельность на уроке… 6. Какие виды работ вызвали затруднения и требуют повторения… 7. Выполнили мы намеченный результат? Слайд: Спасибо за урок! |
учащиеся отвечают по одному предложению по кругу |
|
Приложение 1
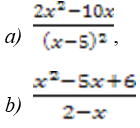
3. Сократите дробь:
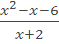
3. Сократите дробь:
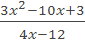
|
|
Задание №1 |
Задание №2 |
Задание №3 |
|
1 вариант |
|
|
|
|
2 вариант |
|
|
|