В настоящее время одной из тенденций улучшения качества образования становится ориентация на развитие творческого потенциала личности ученика на всех этапах обучения в школе, на развитие его творческого мышления, на умение использовать эвристические методы в процессе открытия нового и поиска выхода из различных нестандартных ситуаций и положений.
Система образования в целом направлена на развитие созидающего творческого воображения, но не фантазирования, что было бы существенней для развития личности. Помощь в этом может оказать методика развития творческого воображения и фантазирования.
Содержание методики можно разбить на два класса:
- Приемы и методы активизации творческого воображения и фантазии, преодоления психологической инерции мышления и познавательно-психологических барьеров.
- Приемы и методы генерирования творческих идей и повышения эффективности решения творческих задач.
Приемы и методы первого класса в основном используются для развития компонентов творческого воображения и мышления: гибкости, оригинальности, переключаемости внимания, памяти и др. Методы второго класса позволяют получать фантастические идеи путем целенаправленного преобразования исходной ситуации.
В Межвузовском научно-образовательном центре инженерного творчества Московского государственного индустриального университета (МНОЦИТ МГИУ) разработаны и успешно реализуются теория и практика современного многоуровневого непрерывного креативного образования НФТМ-ТРИЗ – система непрерывного формирования творческого мышления и развития творческих способностей обучаемых (дошкольников, учащихся, студентов и специалистов) с использованием интеллектуальных инструментов теории решения изобретательских задач Г. С. Альтшуллера). Под руководством М. М. Зиновкиной создана научно-педагогическая школа, развивающая основные научные направления современного креативного образования.
Особенность педагогической системы многоуровневого непрерывного креативного образования НФТМ-ТРИЗ состоит в том, что обучающийся из объекта обучения становится субъектом творчества, а учебный материал (знания) из предмета усвоения – средством достижения некоторой созидательной цели. Каждый ребёнок талантлив от природы – это исходная позиция системы НФТМ-ТРИЗ. Воспитание личности через творчество – принцип работы по данной технологии, а создание учителем педагогических условий для выявления творческих способностей и их развития – основная задача [1].
Система НФТМ-ТРИЗ основана на поисково-познавательной деятельности человека и направлена на развитие фантазии и творческого воображения, использование учителем её приёмов позволяет достигать глубокого усвоения фактических знаний, формировать стиль мышления, направленный не на приобретение готовых знаний, а на их самостоятельную генерацию, а так же умение видеть, ставить и решать проблемные задачи в нужной области деятельности, умение понимать закономерности, воспитание мировоззренческой установки восприятия жизни как динамического пространства открытых задач [1].
В соответствии с моделью формирования творческой личности учащихся в НФТМ-ТРИЗ необходимо формировать системное, многоэкранное мышление на основе ТРИЗ, преодолевать инерцию мышления, развивать творческое воображение и фантазию, творческие способности, обеспечивать компьютерную интеллектуальную поддержку мышления, овладевать ТРИЗ и другими методами решения творческих задач.
Согласно НФТМ-ТРИЗ основное направление в начальной школе – развитие управляемого творческого воображения и фантазии и пропедевтика ТРИЗ, то есть подготовка сознания ребенка к дальнейшему восприятию ТРИЗ.
Процесс решения любой творческой задачи достаточно сложен. В процессе решения зачастую возникают психологические барьеры, что толкает на принятие неэффективных решений. Психологическая инерция – привычка к стандартным действиям в типовых ситуациях или упорное стремление человека думать и действовать в соответствии с выработанными и приобретенными привычками и представлениями. Это не случайное, а закономерное явление, присущее людям. А воображение – это качество, заложенное в каждом человеке от рождения, которое с возрастом уходит, если с ним не работать.
Можно и нужно научиться преодолевать психологическую инерцию и развивать свое творческое воображение. Для этого надо стараться развивать такие свойства своего мышления, как нешаблонность, нетривиальность и неинерционность.
Большую роль для всестороннего и гармоничного развития личности среди учебных играют творческие задачи. Для их выполнения требуется изменение изученных правил или самостоятельное составление новых правил, в результате решения которых создаются субъективно или объективно новые системы – информация, конструкции, вещества, явления, произведения искусства.
Диапазон творческих задач необычайно широк по сложности – от решения головоломки до изобретения новой машины или научного открытия, но суть их одна: при решении происходит акт творчества. Вот здесь-то и требуются особые качества ума, такие, как наблюдательность, умение сопоставлять и анализировать, комбинировать, находить связи и зависимости, закономерности и т. д. – всё то, что в совокупности и составляет творческие способности.
Творческие задачи отличаются от тренировочных тем, что задачи как таковой поначалу нет. Ее еще предстоит выявить из проблемной ситуации, которая возникает перед человеком. При этом исходные данные противоречивы и недостоверны. Их надо критически осмыслить и оценить. Как правило, возникает необходимость дополнить их и найти способ разрешения противоречия. Уже с этого момента учащийся включается в творческий процесс, начинает активно думать. В этой поставленной им самостоятельно задаче еще не известно, что необходимо искать, ответ также непредсказуем.
В научном творчестве понятие противоречия является одним из важнейших. Противоречие – это борьба противоположных интересов, желаний или требований, когда одно из них исключает другое.
Противоречие обостряет конфликт, лежащий в основе задачи, до предела, именно благодаря этому облегчается поиск решения. Преодолеть противоречие – значит решить задачу.
В системе НФТМ-ТРИЗ для развития креативности используются задачи открытого типа.
Задачи открытого типа имеют размытое условие, из которого недостаточно ясно как действовать, что использовать при решении, но понятен требуемый результат. Разнообразие путей решения, которые не является «прямолинейными», двигаясь по которым попутно приходиться преодолевать возникающие «препятствия». Вариантов результата решения много, нет понятия «правильное решение»: решение либо применимо к достижению требуемого условия, либо нет. Поэтому, можно говорить об эффективности, оптимальности и оригинальности выбранного решения [2].
Задачи открытого типа предусматривают возможность применения стандартных знаний в нестандартной ситуации, при выполнении таких заданий ученик может проявить способность к логическому и абстрактному мышлению, то есть умение классифицировать, обобщать и проводить аналогии, прогнозировать результат, применяя интуицию, воображение, фантазию, и, главное, способствовать развитию креативности.
Для развития творческих способностей необходимо создание условий. Для сознательного и активного участия в творческой деятельности важен поиск творческих приемов, формирования и совершенствования базовых знаний, умений и навыков, вариативное их использование и на любых уроках. Главное – это создание общей атмосферы творчества и радости.
Инновационные педагогические технологии в многоуровневой системе НФТМ предусматривают реализацию основных дидактических принципов через изменение структуры уроков и их оригинальное наполнение.
Мотивационная аранжировка уроков состоит в том, что специально продуманы системы заданий для поддержания устойчивой положительной мотивации в ходе урока. К концу каждого цикла учебной работы у школьников активно поддерживаются положительные эмоции успеха и желание перейти к следующему этапу работы.
Структура креативного урока существенно отличается от традиционного урока и включает в себя 8 блоков, которые я отразила в разработке урока математики в 3 классе по теме «Деление с остатком». Это урок открытия новых знаний и его основные предметные цели по программе «Школа 2100»:
- Познакомится с делением с остатком.
- Учить производить деление с остатком практическим способом (с помощью рисунка).
- Формировать представление о том, что при делении с остатком остаток должен быть меньше делителя [3].
На уроке предусмотрена работа в группах и парах, а также применяется метод «Мозгового штурма».
Суть метода «Мозгового штурма» – совместный поиск вариантов решения проблем преимущественно на основе интуиции с последующей экспертизой идей, при этом первенство держат задачи неожиданные и фантастические. «Мозговой штурм» является методом, позволяющим снять психологическую инерцию и получить максимальное количество новых идей в минимальное время. При проведении «мозгового штурма» запрещается критика и поощряется любая идея, даже шуточная и явно нелепая.
Класс делится на группы: 3 группы генерирования идей (для поиска вариантов решения задачи) и группа экспертной комиссии (для обработки предложенных вариантов). В каждую группу генерирования идей включается активный учащийся с наиболее развитым воображением. Именно такие ученики могут «вывести из тупика» и вдохнуть свежие силы в процесс.
Блок 1. Мотивация (1,5 мин)
Мотивация – представляет собой специально отобранную систему оригинальных объектов (сюрпризов), способных вызвать удивление учащегося. Этот блок обеспечивает мотивацию обучающегося к занятиям и развивает его любознательность. В данном блоке педагог вызывает интерес к занятию, мотивирует детей на творческую работу.
«Математический фокус»
– Я вас попрошу задумать двузначное число, у которого число десятков на 2 больше числа единиц. Вычесть из него двузначное число, которое записывается теми же цифрами, но в обратном порядке и разделить полученную разность на 9. Сколько у вас получилось?
– Какое число задумали? (опрос учеников класса) Какое число получилось?
Блок 2. Содержательная часть (18 мин)
Содержат программный материал учебного курса и обеспечивают формирование системного мышления и развитие творческих способностей обучающегося.
1. Актуализация знаний. «Весёлые примеры».
- Число ног у паука умножить на количество пальцев на руке у человека. (8•5=40)
- Бабушке 54 года, а внук в 9 раз младше. Сколько лет внуку? (54: 9=6)
- Количество месяцев в году умножить на число голов Змея Горыныча. (12•3=36)
- Любимую оценку ученика умножить на самое маленькое двузначное число. (5•10=50)
- Тетрадь стоит 23 рубля. Сколько будут стоить 2 таких тетради? (23•2 =46)
- Продолжительность урока уменьшить в число дней недели без выходных. (45:5=9)
- Половину рубля уменьшить в число хвостов у 10 котов. (50:10=5)
- Ребята, работаем по группам. На карточках задания (Рис. 1)

Рис. 1. Задание на карточках
Выполняя эти задания, к какому арифметическому действию мы сегодня больше всего склоняемся, назовите тему урока? (Деление)
- Расскажите, что вы знаете о делении?
- Но деление мы уже изучали, какой вопрос у вас возникает? (Мы должны узнать что-то новое о делении).
- У тренера есть 14 теннисных мячей. Он хочет раздать их ребятам, чтобы у всех было равное количество. В первый день на тренировку пришли двое. По сколько мячей они получили?
- На следующий день пришли трое ребят. По сколько мячей они получили? (Не делятся!)
«Мозговой штурм»
- Подумайте в группах, как можно поделить мячи. И все свои варианты, даже самые невероятные запишите на листок. Каждая из групп попробует поделить на разное количество ребят: на 3, 4 и 5.
- Вспомним общие правила генерирующего этапа «Мозгового штурма»:
1. Запрет критики.
2. Запрет обоснования выдвигаемых идей.
3. Поощрение всех идей, даже нереальных и фантастических.
После поиска вариантов решения задачи листки с записями помещаются под документ-камеру и обсуждаются экспертами.
- Проверим, как можно поделить, проведя эксперимент.
Выходят ученики, которые предложили интересные идеи решения. Один из них тренер, он раздает мячи.
Эксперимент: Как 14 мячей разделить между 3 учениками? (Раздаем каждый раз по 1 мячу – поровну).
- Сколько мячей осталось у тренера? (2)
- Запишем решение в тетрадях в виде рисунка (Рис.2).

Рис. 2. Схематичное решение задачи
- Какое число мячей было? (14).
- Между сколькими учениками делили? (3).
- Что получилось?
- Какое количество мячей разделили на 3 без остатка? (12) Почему? Что важно знать при делении? (таблицу ×)
Запись на доске: 14 : 3 = 4 (ост. 2)
- Постарайтесь объяснить запись. Что обозначает каждое число в этой записи? (Число 14 обозначает количество всех теннисных мячей, число 4 количество мячей, выданных каждому игроку, число 3 количество игроков, которым досталось по 4 мяча, число 2 записанное в скобках,- мячи, которые остались не поделёнными (у тренера). 14 разделить на 3, получится 4 и в остатке 2.)
- Попробуйте прочитать это выражение, используя названия компонентов. (Делимое 14, делитель 3, частное 4, остаток 2).
- Так какая тема урока? (Деление с остатком)
- Теперь разделим 14 мячей между 4 учениками. Сделаем рисунок и запишем выражение в тетрадь.
Один ученик работает у доски.
- Разделим 14 мячей между 5 учениками – самостоятельно.
Блок 3. Психологическая разгрузка (1,5 мин)
Психологическая разгрузка реализуется через упражнения по гармонизации развития полушарий головного мозга, через аутотренинг, через систему спортивно-эмоциональных игр, театрализацию и др.
Танцевальная видеофизминутка.
Блок 4. Головоломка (2,5 мин)
Одним из важнейших элементов структуры современного креативного урока в системе НФТМ является творческая деятельность учащихся с системой натуральных объектов – головоломок, в конструкции которых реализована остроумная изобретательская идея.
Головоломка «Неугомонный квадрат».На партах наборы фигур из бумаги (Рис.3)
- Перед вами 5 элементов, требуется собрать квадрат. (Работа в парах)
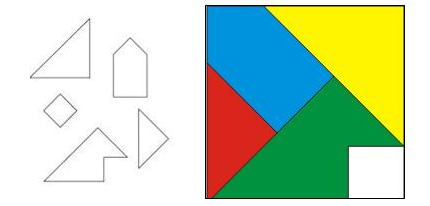
Рис. 3. Головоломка «Неугомонный квадрат»
Блок 5. Интеллектуальная разминка (2,5 мин)
Интеллектуальная разминка, как и головоломки, позволяет обеспечить мотивацию учащихся и включить их в творческую деятельность на уроке. Главная функция интеллектуальной разминки состоит в подготовке к выполнению сложных заданий через осознание значимости правильно проведенного анализа информации.
- Выполним задание № 6 стр.61 учебника.
- Денис, Мишка и Костик участвовали в соревнованиях по стрельбе из лука, и один стал победителем. Джон спросил у них, кто это был. Денис сказал: «Это не я!». Мишка сказал: «Это был я!». Костик: «Не Денис!». Кто же победил в соревнованиях, если только двое из ребят сказали правду? [4]
Блок 6. Содержательная часть (12 мин)
- Прочитай и объясни записи (№ 2 стр.60)
Коля: 14:4=3 (ост.2) Миша: 14:3=4 (ост.2) Петя: 14:2=7 (ост.0)[4]
- Почему в последней записи в остатке записан 0?
- Можно ли было сделать такую запись: 14:2=7?
- Кто из ребят сумел поделить мячи без остатка?
- Прочитайте правило на стр.60: Когда одно число без остатка делится на другое, то это значит, что в остатке получается ноль, и такой остаток обычно не записывается.[4]
- Выполним деление 8:3, возьмем 8 карандашей и разложим их по 3. Сделаем рисунок и запись.
- Теперь 7:2 и 10 :4. Выполните задание в парах сначала с помощью карандашей.
- Выполняем №3 стр.60, сделав рисунки.
15:3 16:3 19:3 11:3
- Сравни делитель и остатки. Можно ли к некоторым выражениям сделать такие рисунки и записи (Рис.4):

Рис. 4. Схематичное решение задачи № 3
- Может ли остаток быть равен делителю или быть больше него?
-Прочитайте правило на стр. 61: Остаток при делении всегда должен быть меньше делителя. Если остаток больше или равен делителю, то, значит, мы неверно нашли частное [4].
- Запишите домашнее задание: №4, 5 стр.61 и №7 стр.61 - по желанию.
Блок 7. Компьютерная интеллектуальная поддержка (5 мин)
Компьютерная интеллектуальная поддержка (КИП) продолжает и углубляет идеи, заложенные в мотивационных заданиях, заданиях типа головоломок, заданиях интеллектуальной разминки и др.
- Выполняем работу в парах на ноутбуках мобильного класса в программе «Мир информатики» (Рис.5).
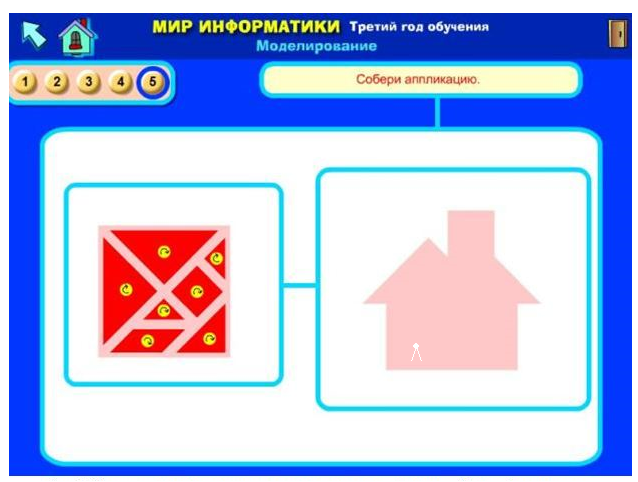
Рис. 5. Задание по моделированию на компьютере в программе «Мир информатики»
Блок 8. Резюме (2 мин)
Этот блок обеспечивает обратную связь с учащимися на уроке и предусматривает качественную и эмоциональную оценку учащимся самого урока. На этом этапе учитель подводит краткие итоги урока и устно осуществляет обратную связь с учащимися, выявляет их мнение об уроке.
- Чему научились на уроке?
- Что понравилось на уроке?
- Закройте глаза. Поднимите руки те, кому урок понравился. Теперь те, кому что-то не понравилось в уроке.
Учителю важно учить детей мыслить, а именно на креативных уроках ученики находятся в постоянном поиске, открывают для себя что-то новое. Детское творчество неисчерпаемо и задача учителя – создать условия для творческой деятельности, стимулирующей нестандартное мышление. Использование системы НФТМ-ТРИЗ (непрерывное формирование творческого мышления и развития творческих способностей) помогает ребёнку учиться легко, с удовольствием и, самое главное, осмысленно.
Ссылки на источники
- Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: Прикладной курс научного творчества: Учебное пособие. – Киров: АНОО «Межрегиональный ЦИТО», 2013. – 212 с.
- Утёмов В. В. К вопросу формирования инновационного мышления учащихся общеобразовательной школы посредством решения задач открытого типа. Вестник Вятского государственного гуманитарного университета, Т. 3. № 2, 2010 – С. 31-33.
- Козлова С. А., Рубин А. Г., Горячев А. В. Математика 3 класс: Методические рекомендации для учителя по курсу математики с элементами информатики. – Москва: Баласс, 2012 – 156 с.
- Козлова С. А., Рубин А. Г., Горячев А. В. Математика 3 класс: Учебник. Часть 1. – Москва: Баласс, 2012 – 60-61 с.
