Войти / Зарегистрироваться

Методическая разработка урока математики "Признаки равенства треугольников"

Получить свидетельство
Автор: Кудинова Ирина Константиновна
Форма проведения: круговая тренировка.
После вступительного слова учителя и математической разминки, обучающиеся делятся на группы и начинают выполнять задания в разной последовательности: 1-ая группа решает задачи по готовым чертежам в парах, 2-ая группа – выполняет групповое решение задачи разными способами, 3-я группа – доказывает равенство треугольников учителю (по одному рисунку на каждого), 4-я группа – выполняет тест (индивидуально для каждого). Затем другая последовательность заданий. Двигались против часовой стрелки (так решили). После двух кругов проводила физкультминутку, затем смотрели и слушали проект «Треугольники в природе и искусстве», потом продолжали выполнять задания.  В итоге, каждая группа выполняет 4 вида заданий. За каждый этап команде дается кусочек пазла, который надо собрать в конце. Это разрезанная инструкция по изготовлению математической игрушки. В конце урока совместное подведение итогов и выполнение совместного проекта «Игрушка Флексагон».
Деление на группы можно провести разными способами. У меня были блицопросы за 1 минуту на предыдущем уроке. Набрал наибольшее количество баллов – ты командир (таких командиров четверо – по количеству команд), выбирает из тех, кто набрал чуть меньше (их тоже четверо), следующий выбирает из тех учеников, которые набрали меньше его и т.д.
Цели урока:
Обучающие: закрепить знания о геометрической фигуре – треугольник, видах треугольников, уметь решать задачи прикладного характера с
применением определения, свойств треугольника и признаков равенства треугольников.

Развивающие: способствовать формированию умений применять приемы сравнения, обобщения, выделения главного; развитие грамотной математической письменной и устной речи учащихся; развитие творческих представлений, математического мышления.

Воспитывающие: формирования интереса учащихся к математике через углубление их представлений о практическом значении треугольников и применении их в окружающем мире; развитие деловых качеств личности, личностного самосовершенствования через представление проектов.
Оборудование: проектор, экран, компьютер, презентации, дидактический материал.
Время проведения: 2 академических часа.
Ход урока:

1. Организационный момент:

Сегодня один из обобщающих уроков по следующей теме

 

 

 

«Треугольники».

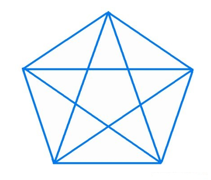
Треугольник в  геометрии играет особую роль. Без преувеличения можно сказать, что почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник. Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет. Треугольник неисчерпаем – постоянно открываются его новые свойства. Чтобы рассказать обо всех известных его свойствах, необходим том сравнимый по объему с томом Большой энциклопедии. Одни из самых удивительных задач в геометрии – задачи про треугольники. И вот одна из них: сколько треугольников на рисунке?
 
Что является важным при решении задач?
Учащиеся начинают работать в группах.
3. Актуализация опорных знаний.
Работа в парах по готовым чертежам:
Задание 1. На рисунке МP =MT, PK=TK какие точки достаточно соединить, чтобы получились равные треугольники?
 
Задание 2. Проведите отрезок так, чтобы получились равные треугольники.
Проведите два отрезка так, чтобы получились равные треугольники.
Задание 3. На рисунке даны две окружности с общим центром О и равные отрезки АВ и СD. Какие пары точек достаточно соединить, чтобы получились равные треугольники?
 
Решите задачу разными способами: На рисунке изображены два равных треугольника: АВС=ВАD. Докажите, что АОС= ВОD.
 
Ребята, исходные данные у всех были одинаковыми, и цель у всех была одна. А вот пути решения были разными.
Учащиеся по группам указывают различные способы доказательства. Наиболее интересные способы записываем на доске в конце урока.
Физминутка
Гимнастика для глаз
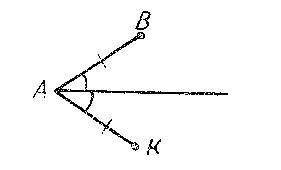
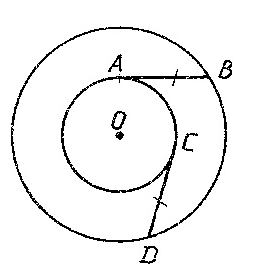
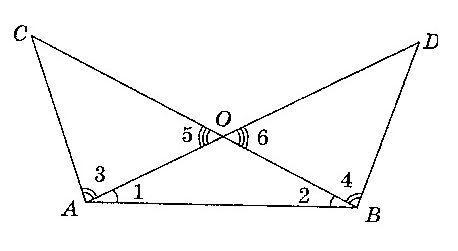
  1. Сделайте 4-6 движений глазами влево – вправо, вверх – вниз.
  2. Посмотрите вдаль на какой-нибудь предмет, затем на предмет, находящийся рядом. И так 6-10 раз.
  3. Подержите несколько секунд на висках пальцы рук.
Упражнения для позвоночника
Воздействуя на позвоночник, мы улучшаем функции практически всех внутренних органов. Дышим только через нос, тем самым улучшаем рефлекторный приток крови к мозгу.
  1. Подбородок скользит вниз, касаясь груди. Голова следует за подбородком. Шея несколько напряжена.
  2. Наклоны головы влево и вправо с фиксацией плеч. Движения плавные, плечи абсолютно неподвижные.
Выступление учащегося с проектом «Треугольники в природе и искусстве» (приложение 1)
  • Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, т. к. эта фигура всегда имела широкое применение в практической жизни.
  • Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник (Слайд).
  • Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта. Еще в древности стали вводить некоторые знаки обозначения для геометрических фигур (Слайд ).
  • В Древней Греции уже был известен способ построения прямоугольного треугольника на местности. Для этого использовали веревку, на которой были завязаны 13 узелков, на одинаковом расстоянии друг от друга (Слайд).
  • Люди научились определять расстояние до звезд. В этом им также помогли треугольники (Слайд ).
  • Треугольники помогали выигрывать военные сражения. О способе построения войск клином заслушайте сообщение (Слайд).
  • Применение равностороннего треугольника и треугольных чисел: расстановка кеглей в боулинге и шаров в бильярде (Слайды ).
  • Картинка – иллюзия треугольник Пенроуза (Слайд).
  • В небе созвездие Треугольник (Слайд).
  • Загадочный Бермудский треугольник (Слайд).
  • Горестный солдатский треугольник (Слайд)
  • Треугольники помогают создавать прекрасное. Это заметил А.С.Пушкин. (Слайд).
  • Треугольники помогают в создании красивого узора, орнамента. Посмотрите на паркет (Слайд).
  • Музыкальный треугольник (Слайд).
  • Инженеры любят треугольник за его крепость и используют при создании конструкций, например Эйфелевой башни и Останкинской телебашни, различных мостов и вышек (Слайды ). В создании таких сооружений помогла молодая наука бионика, которая изучает живую природу с целью использования полученных знаний в практической деятельности человека. Бионика создает инновационный архитектурный стиль, берущий все самое лучшее от природы: рельеф, контуры, формы.
Задание для 3-й группы:
Сформулируйте первый признак равенства треугольников. 
Сформулируйте второй признак равенства треугольников. 
Сформулируйте третий признак равенства треугольников. 
Интерактивная  презентация  «Равные треугольники» (приложение 2)
Докажите равенство следующих треугольников:
 
5. Обобщающий тест по теме «Треугольники» (приложение 3)
                                                            Вариант 1
 

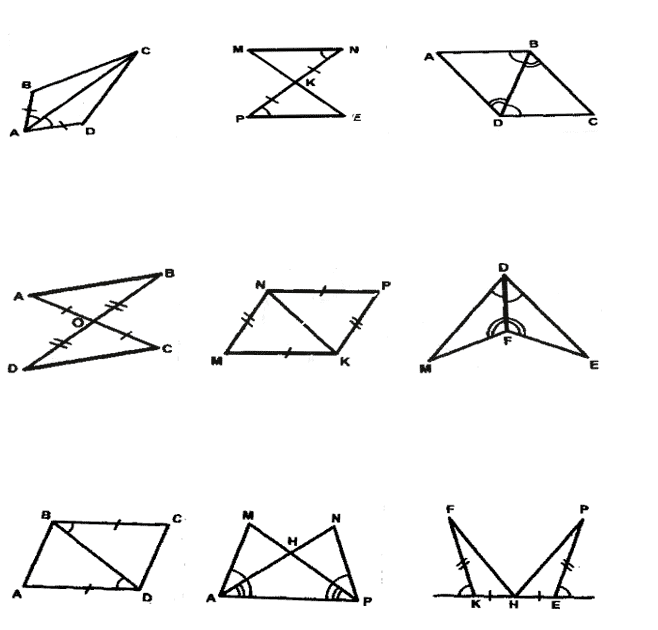
1.Укажите на каких  рисунках есть равные треугольники

  
  1. ΔDЕА = ΔFЕВ. Тогда ΔАЕВ :

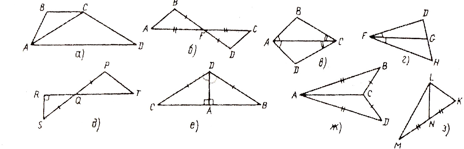а) равносторонний;            б) разносторонний;       

  в) равнобедренный.

 

  
  1. В треугольнике АВС  

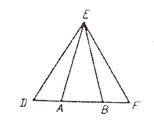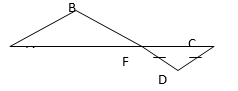
 ÐАВС = 90°, ÐВСД = 64°. Найти  ÐДАВ

 

  
  1. Треугольник RST- равнобедренный.

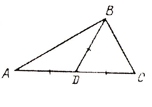Определите Ð1,

если Ð2  =112°

  

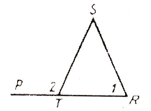5. Если у треугольника два внешних угла равны , то он является:

а) равносторонним; 

б) равнобедренным;  

в) произвольным.

 

 

 

6. ΔАВС – равносторонний. Найдите его углы.

 

7. Могут ли в треугольнике два угла быть прямыми?

 

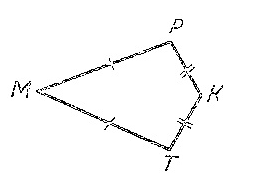
8. ΔCDF равнобедренный,

АВ ‖CD . Укажите , какому углу ΔABF  равен угол CDF треугольника CDF

      
 
                                                            Вариант 2
 

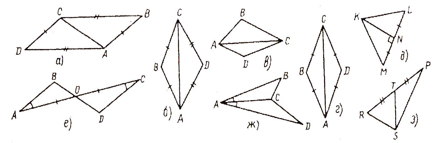
1.Укажите на каких  рисунках есть равные треугольники

  

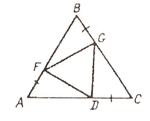
2.ΔABC- равносторонний, AF=BG=CD. Тогда ΔFGD :

а) равносторонний;            б) разносторонний;       

  в) равнобедренный.

 

  

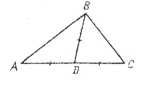
3.В треугольнике АВС  

 ÐА = 37°, ÐС = 53°. Найти  ÐАВС

 

  

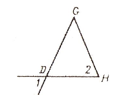
4.Треугольник DGH - равнобедренный.

Определите Ð2,

если Ð1  =67°

  

5. Если у треугольника один из внешних углов - острый , то треугольник:

а) остроугольный; 

б) прямоугольный;  

в) тупоугольный.

 

6. ΔАВС – прямоугольный  равнобедренный.(АВ=ВС) Найдите его углы.

 

7. Могут ли в треугольнике два угла быть тупыми?

 

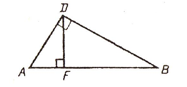
8. DF –высота прямоугольного Δ ADB . Укажите , какому углу ΔADF  равен угол DBF треугольника ABD.

                

                                                                                               
 
6. Проектная деятельность в рамках урока.
Игрушка "Флексагон".
Существует интересная геометрическая игрушка, которая состоит из треугольников и меняется, "выворачиваясь наизнанку". Это - игрушка "Флексагон". "To flax" означает складываться, гнуться, то есть "Флексагон" - "гнущийся многоугольник". "Флексагон" обладает удивительной способность внезапно менять форму и цвет.
Дается полная инструкция, как изготовить такую игрушку (приложение 4)
Демонстрация игрушки .
 
 7.  Подведение итогов урока. Рефлексия.
 
        На уроке я работал                         
        Своей работой на уроке я              
        Урок для меня показался              
        На уроке я 
        Мое настроение                             
        Материал урока мне был
 
 
Список литературы:
  1. Атанасян, Л.С. Геометрия: Учебник для 7-9 классов средней школы [Текст] / Л.С. Атанасян, В.Ф. Бутузов.- М. : Просвещение, 2006.- 384 с.
  2. Григорьева, Г. И. Нестандартные уроки математики [Текст] / Г. И. Григорьева- Волгоград : Корифей, 2000.- 96 с.
  3. Дроботенко, Н.М. Нестандартный урок математики по теме «Решение задач разными способами». [Текст]  / Н. М. Дроботенко // Начальная школа.- 2005.- №1.- с. 58-61
  4. Кульневич,  С. В. Нетрадиционные уроки [Текст] : Современный урок : часть 2 / С. В. Кульневич, Т. П. Лакоценина. -  ростов-н/Д : Учитель, 2005.
  5. И.А. Резенова "Необычные уроки обычных детей" (http://www.pandia.ru/text/77/204/79470.php)
 
Скачать публикацию

Похожие публикации